Файл: Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины.docx

Задача 6.3

Вариант №	Ток I, А	Ф, мкВб	N
1	3,63	5,79	829
2	3,82	7,31	807
3	2,04	6,45	865
4	2,71	7,59	861
5	2,89	8,52	841
6	3,15	8,18	869
7	3,28	6,64	804
8	3,75	6,66	851
9	3	8,04	879
10	2,95	5,28	830
11	2,4	4,03	867
12	3,97	7,55	821
13	2,27	6,84	863
14	2,18	6,19	846
15	2,1	5,18	812
16	3,23	8,5	866
17	3,07	5,33	819
18	3,98	5,14	822
19	2,5	7,99	842
20	3,63	4,99	802
21	2,06	8,74	861
22	3,67	7,77	864
23	3,31	6,07	876
24	2,08	5,04	819
25	2,09	7,14	816
26	3,49	8,97	814
27	3,24	6,39	844
28	3,5	5,45	808
29	3,97	4,05	809
30	3,53	5,2	802
31	2,43	5,9	817
32	2,49	5,74	861
33	3,44	4,46	878
34	3,84	5,03	864
35	3,69	7,7	853
36	2,6	8,28	810
37	2,71	6,31	841
38	2,83	5,46	818
39	2,12	5,45	838
40	3,6	8,35	825
41	2,48	6,24	852
42	3,79	7,5	830
43	2,03	5,99	805
44	2,91	7,16	877
45	2,78	4,23	853
46	3,94	5,63	824
47	2,69	6,7	851
48	2,03	4,1	868
49	2,59	5,75	838
50	2,3	8,42	874
51	3,98	5,87	816
52	3,98	8,34	826
53	2,95	6,43	802
54	2,92	6,72	842
55	3,76	4,42	817
56	3,51	8,84	822
57	3,2	7,83	857
58	2,58	4,26	819
59	3,03	4,86	849
60	3,41	5,2	850
61	2,87	5	849
62	2,57	7,76	807
63	3,04	4,1	856
64	2,37	5,56	847
65	3,56	6,17	808
66	2,03	8,11	810
67	2,48	8,14	821
68	3,4	7,23	840
69	2,33	6,44	857
70	3,69	7,67	806
71	2,06	8,15	844
72	2,9	4,05	823
73	2,51	7,36	819
74	2,33	5,12	839
75	2,77	5,7	877
76	2,13	7,78	876
77	3,61	8,73	854
78	3,09	6,68	853
79	2,42	5,44	874
80	2,18	7,29	873
81	2,28	5,81	867
82	2,54	5,28	856
83	3,35	7,03	867
84	3,06	5,62	805
85	2,56	8,53	858
86	2,08	6,04	807
87	2,92	8,32	800
88	3,94	5,85	866
89	2,69	8,74	820
90	3,76	5,98	812
91	2,33	4,41	857
92	2,15	8,59	849
93	3,01	5,54	863
94	3,86	4,92	855
95	2,36	7,33	828
96	2,76	7,38	833
97	2,87	4,94	838
98	3,88	4,64	872
99	3,25	5,34	861
100	3,37	5,09	830

---

---

7. Энергия магнитного поля

Основные формулы

• Энергия W магнитного поля, создаваемого током в замкнутом контуре с индуктивностью L, определяется формулой

,

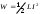где I – сила тока в контуре.

• Объёмная (пространственная) плотность энергии w однородного магнитного поля (например, поля длинного соленоида)

.

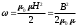• Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

,

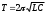где L – индуктивность контура; С – его электроёмкость.

• Связь длины электромагнитной волны с периодом Т и частотой ν колебаний

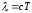или ,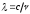

где с — скорость электромагнитных волн в вакууме (с = 3*10⁸ м/с).

• Скорость электромагнитных волн в среде

_{v = c (εμ)0.5,}

где ε – диэлектрическая проницаемость; μ – магнитная проницаемость среды.
Примеры решения задач

Пример 7.1. На стержень из немагнитного материала длиной l = 50 см намотан в один слой провод так, что на каждый сантиметр длины стержня приходится n = 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока I в обмотке равна 0,5 А. Площадь S сечения стержня равна 2 см².

Решение. Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течёт ток I, выражается формулой

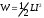. (1)

Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объёма V сердечника: L = μ₀n²V, где μ₀ –магнитная постоянная (₀ = 410^-7 Гн/м). Подставив выражение индуктивности L в формулу (1), получим 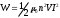. Учтя, что

---

V = lS, запишем

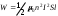. (2)

Сделав вычисления по формуле (2), найдём

W = 62,83 мкДж.

Пример 7.2. По обмотке метрового соленоида со стальным сердечником течёт ток I = 2А. Определить объёмную плотность ω энергии магнитного поля в сердечнике, если число п витков на каждом сантиметре длиныl соленоида равно 7 см^-1.

Решение. Объёмная плотность энергии магнитного поля определяется по формуле

W = ВН/2. (1)

Напряжённость Н магнитного поля найдём по формуле H = nlI. Подставив сюда значения п, lнайдёмколичество витков соленоида (п = 7 см¹, l = 1 м, nl = 700 м^-1) и I, найдём

H = 1400 А/м.

Магнитную индукцию В определим по графику (см. рис. 5.1) зависимости В от Н. Находим, что напряжённости H = 1400 А/м соответствует магнитная индукция B = 1,16 Тл.

Произведя вычисление по формуле (1), найдём объёмную плотность энергии:

W = 812 Дж/м³.

Пример 7.3. На железный сердечник длиной l = 20 см малого сечения (d<l) намотано N = 200 витков. Определить магнитную проницаемость μ железа при силе тока I = 0,4 А.

Решение. Магнитная проницаемость μ связана с магнитной индукцией В и напряжённостью Н магнитного поля соотношением (₀ = 410^-7 Гн/м)

B = μ₀μH. (1)

Эта формула не выражает линейной зависимости В от Н, так как μ является функцией Н. Поэтому для определения магнитной проницаемости обычно пользуются графиком зависимости В(Н) (см. рис. 5.1). Из формулы (1) выразим магнитную проницаемость:

μ = B/(μ₀H). (2)

Напряжённость Н магнитного поля вычислим по формуле (катушку с малым сечением можно принять за соленоид) Н = п1, где п — число витков, приходящихся на отрезок катушки длиной 1 м. Выразив в этой формуле п через число N витков катушки и ее длину l, получим

H = (N/l)I.

Подставив сюда значения N, l и I и произведя вычисления, найдём

H = 400 А/м.

По графику Рис. 5.1 находим, что для железа напряжённости Н = 400 А/м соответствует магнитная индукция B = 0,99 Тл. Подставив найденные значения В и Н, а также значение μ₀ в формулу (2), вычислим магнитную проницаемость:

μ = 1,9695 *10³.
Задача 7.1

Вариант №	l, см	n	Ток I, А	S, см2
1	51,1	24	1,51	2,88
2	52,9	25	0,62	2,69
3	52,6	29	1,92	3,42
4	50,2	28	0,96	3,7
5	51,4	29	1,05	2,06
6	51,7	27	0,55	2,43
7	52,4	30	2,1	3,96
8	51	25	0,58	2,31
9	54,2	28	1,64	2,72
10	53,1	30	0,9	2,15
11	50,1	26	2,48	2,83
12	53,6	28	2,41	2,23
13	52,4	20	0,61	3,33
14	51,5	25	1,3	2,32
15	52,6	25	1,42	2,76
16	53,9	24	1,28	2,69
17	50,9	28	1,6	2,7
18	50,5	26	1,37	2,38
19	52,3	23	1,37	2,17
20	52	30	2,25	3,91
21	50,5	24	0,7	3,71
22	52,4	21	1,72	2,38
23	54,7	29	0,8	3,57
24	51	25	1,75	2,16
25	51,1	28	2,19	2,27
26	52	29	0,76	3,2
27	53,1	24	1,15	2,14
28	53,7	26	0,83	2,01
29	50,9	21	1,94	3,54
30	54,6	29	1,4	2,73
31	54,6	26	0,81	2,14
32	54,4	28	1,27	2,51
33	53,9	21	1,69	2,91
34	53,4	21	2,25	2,37
35	51,3	26	1,05	2,45
36	50,2	26	0,85	2,97
37	54,9	30	1,45	3,97
38	53,1	20	1,99	2,76
39	50,6	21	2,36	3,21
40	52,5	26	1,91	2,31
41	52,6	20	0,52	3,99
42	50,1	27	1,3	2,1
43	53,2	23	2,12	3,95
44	54,3	29	1,54	2,8
45	50,8	26	0,99	2,56
46	51,2	25	1,13	3,37
47	52,6	30	2,02	3,19
48	54,7	24	1,63	3,5
49	51,3	29	1,76	3,12
50	50,1	27	1,78	3,74
51	53,4	26	2,24	2,76
52	54,9	28	2,33	3,86
53	52,4	27	1,53	2,14
54	51	21	1,76	3,48
55	50,4	21	1,97	3,81
56	54,4	24	0,95	2,06
57	51,8	23	0,97	3,57
58	51,3	24	0,53	2,35
59	51	22	0,63	3,32
60	51,9	30	1,13	3,4
61	52,9	27	0,99	3,3
62	51,7	28	1,84	2,78
63	52,5	22	1,91	3,8
64	52,6	24	1,43	3,86
65	50,7	20	2,35	3,06
66	52,2	28	1,63	2,61
67	52,6	27	0,57	2,49
68	50,7	25	2,27	2,68
69	54,4	23	0,72	2,1
70	52	30	2,05	3,69
71	53,7	26	1,68	3,83
72	51,6	25	2,46	2,93
73	50,4	29	1,25	2,45
74	52,1	23	0,76	3,85
75	52,8	30	1,79	2,94
76	54,4	25	0,79	3,31
77	52,7	25	0,62	3,22
78	51,9	26	0,94	3,65
79	51,2	28	0,68	3,99
80	53	28	1,08	2,76
81	54,1	25	0,83	2,43
82	54,4	23	1,24	3,06
83	55	22	1,87	2,93
84	54,7	29	1,84	3,88
85	51,9	22	2,41	2,05
86	52,1	23	1,28	2,97
87	52,8	20	1,94	3,62
88	52,5	22	0,97	2,32
89	50,8	23	1,18	2,58
90	53,9	28	1,94	3,59
91	51,5	29	1,82	2,09
92	50,2	23	1,91	3,27
93	54,8	24	1,31	2,62
94	53,2	23	1,39	3,29
95	52	24	2,27	2,64
96	54,3	23	1,43	2,24
97	52,9	26	1,73	2,17
98	50,8	29	1,58	2,3
99	52,3	24	1,93	3,32
100	50,3	23	0,8	2,84

---

---