Файл: Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины.docx

Задача 2.3

Вариант №	Объём V, см3	Площадь S, см2	Ток I, мкА	Концентрация n, *107 см-3
1	384	252	2,86	6,17
2	385	254	2,73	5,38
3	380	257	2,99	5,45
4	378	256	2,63	6,04
5	385	255	2,06	5,75
6	383	259	2	6,06
7	384	252	2,43	5,34
8	385	254	2,89	5,9
9	393	254	2,64	5,54
10	383	254	2,54	5,33
11	379	258	2,73	5,32
12	395	251	2,4	5,63
13	380	255	2,76	5,65
14	393	250	2,04	6,05
15	384	257	2,83	5,79
16	393	252	2,93	5,89
17	380	255	2,56	6,04
18	393	251	2,18	5,61
19	377	260	2,41	6,29
20	390	257	2,3	5,42
21	379	258	2,54	6,23
22	388	259	2,07	5,96
23	390	254	2,16	5,79
24	377	260	2,07	5,42
25	377	256	2,96	5,81
26	384	253	2,08	5,32
27	375	260	2,97	5,83
28	384	259	2,61	5,87
29	394	250	2,79	6
30	392	253	2,02	6,15
31	377	255	2,77	5,88
32	380	253	2,45	5,83
33	378	259	2,93	6,22
34	383	250	2,9	6,04
35	380	259	2,9	5,57
36	392	250	2,22	5,68
37	381	258	2,14	5,55
38	382	257	2,17	5,98
39	387	251	2,94	5,48
40	386	255	2,72	6,17
41	378	254	2,59	6,12
42	378	259	2,06	5,88
43	380	254	2,19	6,19
44	388	254	2,58	5,71
45	380	254	2,47	5,88
46	379	257	2,13	5,93
47	380	255	2,69	5,35
48	389	259	2,18	5,83
49	395	259	2,97	6,07
50	380	254	2,04	6,03
51	388	251	2,08	5,47
52	376	252	2,94	5,84
53	381	259	2,6	6,24
54	377	256	2,77	6,04
55	394	260	2,44	5,81
56	384	260	2,85	6,22
57	388	251	3	5,75
58	393	257	2,04	5,54
59	389	259	2,31	5,41
60	386	256	2,1	5,43
61	394	257	2,81	5,92
62	394	257	2,3	5,97
63	392	259	2,34	5,56
64	375	252	2,93	5,71
65	386	251	2,91	5,93
66	388	257	2,88	5,98
67	380	253	2,61	5,73
68	393	250	2,04	6,03
69	395	256	2,54	5,64
70	393	255	2,99	5,52
71	379	255	2,22	5,97
72	380	254	2,71	5,57
73	377	256	2,76	5,99
74	395	258	2,13	5,49
75	390	255	2,64	5,64
76	392	260	2,89	5,36
77	378	258	2,25	6,19
78	390	251	2,81	5,65
79	393	256	2,38	6,23
80	386	260	2,72	6,24
81	389	252	2,14	5,84
82	383	252	2,94	5,96
83	378	250	2,37	5,38
84	393	256	2,5	5,86
85	384	250	2,36	5,85
86	392	253	2,55	6,05
87	389	258	2,57	5,68
88	382	252	2,94	5,72
89	385	259	2,47	6,1
90	390	257	2,85	5,48
91	382	254	2,73	5,45
92	379	260	2,11	6,23
93	377	250	2,57	6,11
94	388	258	2,62	5,89
95	393	252	2,5	5,91
96	376	258	2,52	5,9
97	379	256	2,89	5,83
98	376	257	2,74	6,01
99	381	255	2,74	5,66
100	381	250	2,3	5,32

---

---

3. Магнитное поле постоянного тока

Основные формулы

 Закон Био – Савара – Лапласа. Вектор магнитной индукции

dB = ₀dl r I/4π r,

где dB – магнитная индукция поля, создаваемого элементом проводника с токомi;  – магнитная проницаемость среды, в которой расположен проводник с током; ₀ – магнитная постоянная (₀ = 4 10^-7 Гн/м); dl – вектор, равный по модулю длине dlпроводника и совпадающий по направлению с током (элемент проводника); I – сила тока; r – радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора dB выражается формулой

dB = ₀dlIsinα/4π r²,

где  – угол между векторами dl и r.

 Магнитная индукция В связана с напряжённостью Н магнитного поля (в случае однородной, изотропной среды) соотношением

B = ₀ Н

или в вакууме

B₀ = ₀ Н.

 Магнитная индукция в центре кругового проводника с током I

B = ₀ I/ (2R),

где R — радиус кривизны проводника.

 Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током I,




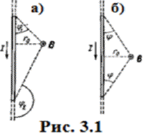
Рис. 3.1
B = ₀ I/ (2πr),

где r – расстояние от оси проводника.

 Магнитная индукция поля, создаваемого на расстоянии r₀ от отрезка проводника с током I

B = ₀ I (cosφ₁ - cosφ₂) / (4π r₀),

Обозначения ясны из рис. 3.1, а). Вектор индукции В перпендикулярен плоскости чертежа, направлен к нам и поэтому изображён точкой.

При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция (рис. 3.1, б), значения косинусов равны, а знак разный, то есть

---

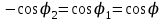и, следовательно,

B = ₀ Icosφ/ (2πr₀)

 Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси),



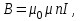
где п — число витков, приходящихся на единицу длины соленоида; I– сила тока в одном витке.

 Принцип суперпозиции магнитных полей:

магнитная индукция В результирующего поля равна векторной сумме nмагнитных индукций В₁, В₂, ..., В_n складываемых полей, т. е.

В = Σ В_i,

где суммирование ведётся по всем nполям.

В частном случае, при наложении двух полей с магнитной индукцией В₁ +В₂, результирующая индукция Вравна

В = В₁ +В₂

а модуль магнитной индукции равен



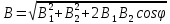
где φ – угол между векторами В₁ и В₂.
Примеры решения задач


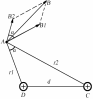Рис. 3.2
Пример 3.1. Два параллельных бесконечно длинных провода (рис 3.2), по которым текут в одном направлении токи I = 60А, расположены в точках D и С. Расстояние между проводами d = 10см. Определить магнитную индукцию В в точке А, отстоящей от одного проводника на расстоянии г₁ = 5 см и от другого – на расстоянии r₂ = 12см.

Решение. Для нахождения магнитной индукции в указанной точке А (рис. 3.2) определим направления векторов индукций В₁ и В₂ полей, создаваемых каждым проводником в отдельности, и сложим их геометрически, т. е. B = B₁+B₂, где B₁ и B₂ вектора. Модуль индукции найдём по теореме косинусов, согласно которой квадрат любой стороны треугольника равен сумме квадратов двух других сторон плюс или минус удвоенное произведение этих сторон на косинус угла между ними. Знак «+» надо брать, когда противолежащий угол, как в нашем случае, тупой, а знак «-», когда угол острый. Итак, имеем:

B = (B₁+B₂

---

+2B₁B₂cosα)^0.5. (1)

Значения индукций B₁и В₂ выражаются через силу тока I и расстояния r₁ и r₂ от провода до точки, индукцию в которой мы вычисляем, имеем:

B₁ = ₀I / (2π r₁),

B₂ = ₀I / (2π r₂),

где ₀ = 4 10 ^-7 Гн/м.

Подставляя выражения B₁и В₂в формулу (1) и вынося ₀I / (2π) за знак корня, получим
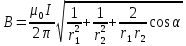(2)

Убедимся в том, что правая часть этого равенства даёт единицу магнитной индукции (Тл):



Откуда следует, что



Вычисляем cos. Заметим, что  = ∠ADC. Поэтому по теореме косинусов запишем d² 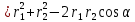, где d– расстояние между проводами. Отсюда

.

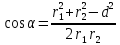Подставив данные, вычислим значение косинуса: cos = 0,575.

Подставив в формулу (2) значения ₀, I, r₁, r₂и cos , найдём

В = 308,54 мкТл.

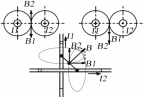Рис 3.3
Пример 3.2. По двум длинным прямолинейным проводам, находящимся на расстоянии r = 5 см друг от друга в воздухе, текут токи I₁ = 10А, I₂ = 12А. Определить магнитную индукцию Вполя, создаваемого токами в точке а = 0,55rот левого провода для случаев: 1) провода параллельны, токи текут в одном направлении (рис. 3.3, а); 2) провода параллельны, токи текут в противоположных направлениях (рис. 3.3, б); 3) провода перпендикулярны, направление токов указано на рис. 3.3, в, в этом случае точка а лежит на диагонали квадрата со стороной r на расстоянии а = 0,55rот вертикального провода.

Решение: Результирующаяиндукция магнитного поля равна векторной сумме: B = B₁+B₂, где B₁ – индукция поля, создаваемого током I₁;В

---