Файл: Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 55
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
U1 = 1,02 * 46,95 = 47,89В.
4. Разность потенциалов UАВ между точками А и В при отключённом вольтметре равна произведению неизвестного тока I3 в новой неразветвленной части цепи, на половину сопротивления потенциометра, т. е. UАВ = I3 RП/2.Ток I3 в новой неразветвленной части цепи равен
I3 = Е / (RП + r),
следовательно выражение для разности потенциалов или для напряжения UАВ между точками А и В имеет вид
UАВ = Е RП / (RП + r)/2
Подставив сюда значения величин ε, rи RПполучим
UАВ =151,94 * 103,51/ (103,51 + 50,04)/2 = 204,85В.
Задача 1.3

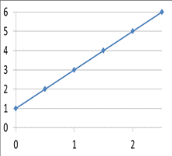
Рис. 1.2
Пример 1.3. Сила тока в проводнике сопротивлением R = 24,39 Ом нарастает в течение времени Δt = 3,87 с по линейному закону от I0 = 3,78 до Imax = 8,54 А (рис. 1.2). Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду, и Q2 - за оставшееся время, а также найти отношение этих количеств теплоты Q2/Q1.
Решение. Закон Джоуля - Ленца Q = I2Rt применим в случае постоянного тока (I= const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде
dQ = I2Rdt. (1)
Здесь сила тока I является некоторой функцией времени. В нашем случае
I = I0+kt, (2)
где
k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:
k = ΔI/Δt.
С учётом равенства (2) формула (1) примет вид
dQ = R (I0+kt)2 dt. (3)
Для определения количества теплоты, выделившегося за конечный промежуток времени Δt, выражение (3) следует проинтегрировать в пределах от t1до t2:
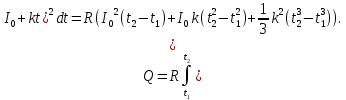
При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t1= 0, t2 = 1 с и, следовательно,
Q1 =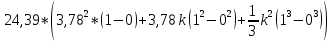 = 86,67 Дж,
= 86,67 Дж,
а за оставшееся время - пределы интегрирования t1 = 1 с, t2 = 2,5 с и тогда
Q2 = 630 Дж.
Следовательно,
Q2/Q1 = 7,27,
т. е. за оставшееся время выделится теплоты в 7,27 раз больше, чем за первую секунду.
Задача 1.1
Задача 1.2
Задача 1.3
Основные формулы
j = en,
где е - элементарный заряд.
J = γE,
где γ - удельная проводимость проводника; Е - напряжённость электрического поля.
w = γE2,
где w- объёмная плотность тепловой мощности.
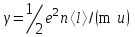
где е и т - заряд и масса электрона; п - концентрация электронов; <l>- средняя длина их свободного пробега; и - средняя скорость хаотического движении электронов
ε = α(Т1- Т2) ,
где α- удельная термо-ЭДС; (Т1- Т2) - разность температур спаев термопары.
m = kQ,,
где m - масса вещества, выделившегося на электроде при прохождении через электролит электрического заряда Q; k - электрохимический эквивалент вещества.
Второй закон
k = M/ (FZ),
где F - постоянная Фарадея (F = 96,5кКл/моль); М - молярная масса ионов данного вещества; Z - валентность ионов.
Объединённый закон,
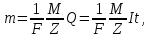
где I - сила тока, проходящего через электролит; t - время, в течение которого шёл ток.
b = <υ>/E,
где <υ>- средняя скорость упорядоченного движения ионов; Е напряжённость электрического поля.
j = Qn(b++b-)E,
где Q -заряд иона; п- концентрация ионов;
b+и b- - подвижности соответственно положительных и отрицательных ионов.
jнac = Qn0d,
где п0- число пар ионов, создаваемых ионизатором в единице объёма в единицу времени; d - расстояние между электродами.
n0 = N/(Vt), где N - число пар ионов, создаваемых ионизатором за время t в пространстве между электродами; V- объём этого пространства.
Примеры решения задач


Рис. 2.1
Пример 2.1. Ток I, равный 16 А, течёт по проводнику длиной l, изготовленному из материала №3 таблицы 2.1(железо), диаметр d сечения проводника равен 0,6 мм,. Определить сpeднюю скорость <υ>направленного движения электронов, считая, что концентрация n свободных электронов равна концентрации п' атомов проводника.
Решение. Средняя скорость направленного (упорядоченного) движения электронов определяется по формуле
<υ> = l/t, (1)
где t- время, в течение которого все свободные электроны, находящиеся в отрезке проводника между сечениями I и II, пройдя через сечение II (рис. 2.1), перенесут заряд Q = eN и создадут ток равный
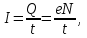 (2)
(2)
где е = 1,6*10-19К - элементарный заряд; N- число электронов в отрезке проводника.
Число свободных электронов в отрезке проводника объёмом V, учитывая, что отрезок проводникаявляется цилиндром, можно выразить следующим образом:
N = nV = nlS, (3)
где S - площадь сечения проводника.
По условию задачи, п = п'. Следовательно,
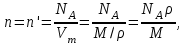 (4)
(4)
где NA = 6,02*1023 к моль-1 - постоянная Авогадро; Vm - молярный объём металла; М = 55,85 - молярная масса металла из таблицы 2.1; ρ - его плотность. Для железа плотность ρ = 7,8*103 кг/м3.
Подставив последовательно выражения п из формулы (4) в равенство (3) и N из формулы (3) в равенство (2), получим
4. Разность потенциалов UАВ между точками А и В при отключённом вольтметре равна произведению неизвестного тока I3 в новой неразветвленной части цепи, на половину сопротивления потенциометра, т. е. UАВ = I3 RП/2.Ток I3 в новой неразветвленной части цепи равен
I3 = Е / (RП + r),
следовательно выражение для разности потенциалов или для напряжения UАВ между точками А и В имеет вид
UАВ = Е RП / (RП + r)/2
Подставив сюда значения величин ε, rи RПполучим
UАВ =151,94 * 103,51/ (103,51 + 50,04)/2 = 204,85В.
Задача 1.3
| Вариант | R | t | Io | Imax |
| 76 | 24,39 | 3,87 | 3,78 | 8,54 |


Рис. 1.2
Пример 1.3. Сила тока в проводнике сопротивлением R = 24,39 Ом нарастает в течение времени Δt = 3,87 с по линейному закону от I0 = 3,78 до Imax = 8,54 А (рис. 1.2). Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду, и Q2 - за оставшееся время, а также найти отношение этих количеств теплоты Q2/Q1.
Решение. Закон Джоуля - Ленца Q = I2Rt применим в случае постоянного тока (I= const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде
dQ = I2Rdt. (1)
Здесь сила тока I является некоторой функцией времени. В нашем случае
I = I0+kt, (2)
где
k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:
k = ΔI/Δt.
С учётом равенства (2) формула (1) примет вид
dQ = R (I0+kt)2 dt. (3)
Для определения количества теплоты, выделившегося за конечный промежуток времени Δt, выражение (3) следует проинтегрировать в пределах от t1до t2:
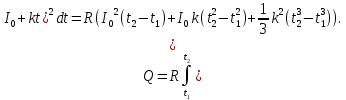
При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t1= 0, t2 = 1 с и, следовательно,
Q1 =
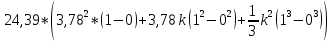 = 86,67 Дж,
= 86,67 Дж,а за оставшееся время - пределы интегрирования t1 = 1 с, t2 = 2,5 с и тогда
Q2 = 630 Дж.
Следовательно,
Q2/Q1 = 7,27,
т. е. за оставшееся время выделится теплоты в 7,27 раз больше, чем за первую секунду.
Задача 1.1
| Вари- ант | Фамилия, имя, отчество | R | U0 | U | t | |||||
| 76 | Матаевский Семен Константинович | 3,02 | 1,58 | 4,58 | 20,53 | |||||
Задача 1.2
| Вариант | R | ЭДС | r | Rв |
| 76 | 103,51 | 151,94 | 50,04 | 505,63 |
Задача 1.3
| Вариант | R | t | Io | Imax |
| 76 | 24,39 | 3,87 | 3,78 | 8,54 |
2. Постоянный ток в проводящей среде
Основные формулы
-
Плотность тока j, средняя скоростьупорядоченного движения носителей заряда и их концентрация n связаны соотношением
j = en
где е - элементарный заряд.
-
Закон академика Петрова-Ома в дифференциальной форме
J = γE,
где γ - удельная проводимость проводника; Е - напряжённость электрического поля.
-
Закон Джоуля - Ленца в дифференциальной форме
w = γE2,
где w- объёмная плотность тепловой мощности.
-
Удельная электрическая проводимость
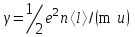
где е и т - заряд и масса электрона; п - концентрация электронов; <l>- средняя длина их свободного пробега; и - средняя скорость хаотического движении электронов
-
Термоэлектродвижущая сила, возникающая в термопаре,
ε = α(Т1- Т2) ,
где α- удельная термо-ЭДС; (Т1- Т2) - разность температур спаев термопары.
-
Законы электролиза Фарадея. Первый закон
m = kQ,,
где m - масса вещества, выделившегося на электроде при прохождении через электролит электрического заряда Q; k - электрохимический эквивалент вещества.
Второй закон
k = M/ (FZ),
где F - постоянная Фарадея (F = 96,5кКл/моль); М - молярная масса ионов данного вещества; Z - валентность ионов.
Объединённый закон,
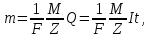
где I - сила тока, проходящего через электролит; t - время, в течение которого шёл ток.
-
Подвижность ионов
b = <υ>/E,
где <υ>- средняя скорость упорядоченного движения ионов; Е напряжённость электрического поля.
-
Закон академика Петрова-Ома в дифференциальной форме для электролитов и газов при самостоятельном разряде в области, далекой от насыщения,
j = Qn(b++b-)E,
где Q -заряд иона; п- концентрация ионов;
b+и b- - подвижности соответственно положительных и отрицательных ионов.
-
Плотность тока насыщения
jнac = Qn0d,
где п0- число пар ионов, создаваемых ионизатором в единице объёма в единицу времени; d - расстояние между электродами.
n0 = N/(Vt), где N - число пар ионов, создаваемых ионизатором за время t в пространстве между электродами; V- объём этого пространства.
Примеры решения задач


Рис. 2.1
Пример 2.1. Ток I, равный 16 А, течёт по проводнику длиной l, изготовленному из материала №3 таблицы 2.1(железо), диаметр d сечения проводника равен 0,6 мм,. Определить сpeднюю скорость <υ>направленного движения электронов, считая, что концентрация n свободных электронов равна концентрации п' атомов проводника.
Решение. Средняя скорость направленного (упорядоченного) движения электронов определяется по формуле
<υ> = l/t, (1)
где t- время, в течение которого все свободные электроны, находящиеся в отрезке проводника между сечениями I и II, пройдя через сечение II (рис. 2.1), перенесут заряд Q = eN и создадут ток равный
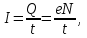 (2)
(2)где е = 1,6*10-19К - элементарный заряд; N- число электронов в отрезке проводника.
Число свободных электронов в отрезке проводника объёмом V, учитывая, что отрезок проводникаявляется цилиндром, можно выразить следующим образом:
N = nV = nlS, (3)
где S - площадь сечения проводника.
По условию задачи, п = п'. Следовательно,
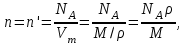 (4)
(4)где NA = 6,02*1023 к моль-1 - постоянная Авогадро; Vm - молярный объём металла; М = 55,85 - молярная масса металла из таблицы 2.1; ρ - его плотность. Для железа плотность ρ = 7,8*103 кг/м3.
Подставив последовательно выражения п из формулы (4) в равенство (3) и N из формулы (3) в равенство (2), получим

