Файл: Общие методы моделирования равномерно распределенных случайных чисел.docx

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования «Ижевский государственный технический университет имени М.Т.Калашникова»

Кафедра «Вычислительная техника»

Отчет

по лабораторным работам

по дисциплине

«Моделирование»

на тему: «Общие методы моделирования равномерно распределенных случайных чисел»

Выполнил студент гр. Б19-781-1зу

Пьянков А.О.

Принял доктор технических наук, профессор

Шелковников Е.Ю.
Ижевск 2023

Содержание

Введение

В настоящее время компьютерные модели стали обычным инструментом математического моделирования и применяются в различных областях науки и техники. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования. Компьютерное моделирование является одним из эффективных методов изучения сложных систем.

Компьютерные модели проще и удобнее исследовать в силу их возможности проводить т. н. вычислительные эксперименты, в тех случаях, когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий.

В данном лабораторном практикуме рассматривается вопрос разработки генератора равномерно распределенных случайных чисел. Также сравнение качества разработанного генератора, со встроенными генераторами в языки высокого уровня при помощи специальных эмпирических тестов.

---

Разработка генератора равномерно распределенных случайных чисел.

Цель работы

Целью работы является разработка генераторов равномерно распределенных случайных чисел.

Ход работы

Методы моделирования распределенных случайных чисел:

1. 
   Метод усечения
   

Основан на выборе середины произведения. В начале рекуррентного процесса берется произвольное 2n разрядное число 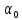. Величина 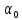возводится в квадрат, который уже состоит из 4n цифр, затем выбирается число 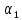из 2n средних цифр, в дальнейшем процесс повторяется.

Недостаток метода – большие отклонения от равномерности.

2. 
   Метод произведений
   

Является некоторым видоизменением метода усечения, но дает значительно лучшие результаты. Выбирается произвольная пара чисел U₀ и U₁ , далее составляется их произведение, и его средние цифры используются в качестве числа U₂. Затем процесс повторяется для U₁ и U₂ с получением числа U₃ и т.д.

3. 
   Линейный конгруэнтный метод
   

Суть метода заключается в вычислении последовательности случайных чисел X n {\displaystyle X_{n}}X_n , полагая X_n+1 = (aX_n + c) modm, где m- модуль (натуральное число, относительно которого вычисляет остаток от деления). X₀ – начальное значение, с – приращение. Эта последовательность называется линейной конгруэнтной последовательностью. Линейная конгруэнтная последовательность периодична с периодом , не превышающем m. Данный алгоритм обеспечивает достаточно большие длины последовательностей случайных чисел. m ⩾ 2 {\displaystyle m\geqslant 2}
1)За основу генератора был выбран «Смешанный конгруэнтный метод».Алгоритм метода записывается в виде формулы:

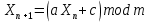, где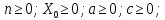

---

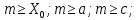
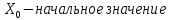
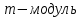
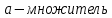
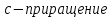
При выборе числа m необходимо учитывать следующие условия:

1) число m должно быть довольно большим, так как период не может иметь больше m элементов;

2) значение числа m должно быть таким, чтобы  вычислялось быстро.

Также стоит учитывать, что младшие двоичные разряды сгенерированных таким образом случайных чисел демонстрируют поведение, далёкое от случайного, поэтому рекомендуется использовать только старшие разряды. В связи с этим, было решено брать 1 разряд из старшей части числа, полученного при помощи . Для выполнения этой операции, была написана функция Digits. Она принимает число 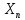и возвращает разряд из старшей части.

Каждое полученное таким образом число, записывается в вектор. Для многократного обращения к одной и той же последовательности, предусмотрена запись и чтение вектора в текстовый файл.

Для того, что бы последовательности с каждой генерацией были разные, начальное значение вычисляется путем простых математических операций с константами и текущим временем операционной системы.

В качестве значений a, c, и m, были взяты константы:

a = 214013, c =4, m = 2147483647. Приведенные константы обеспечивают работу генератора с максимальным периодом. 

Блок схема алгоритма 1




Реализация генератора на С++

//первый генератор

intrandom(_int64 &x)

{

_int64 m = 2147483647; //time(NULL);

_int64 a = 214013;

_int64 c = 4;

x = ((a*x) + c) % m;

returnx;

}
2)За основу генератора был выбран «Квадратный конгруэнтный метод». Алгоритм метода записывается в виде формулы:

• 
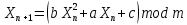
  c и m взаимно простые числа;
  
• 
  b и a-1 кратны всем нечетным простым делителям m;
  
• 
  b четное и b ≡a-1(mod 4), если m кратно 4;
  
• 
  b ≡a-1(mod 2), если m кратно 2;
  
• 
  или d ≡0 или а ≡1 и сb ≡6(mod 9), если m кратно 9
  

---

В качестве значений a, c, b, и m, были взяты константы:

a = 967, c =3041,b =966, m = 14406. Приведенные константы обеспечивают работу генератора с максимальным периодом. 
Блок схема алгоритма 2


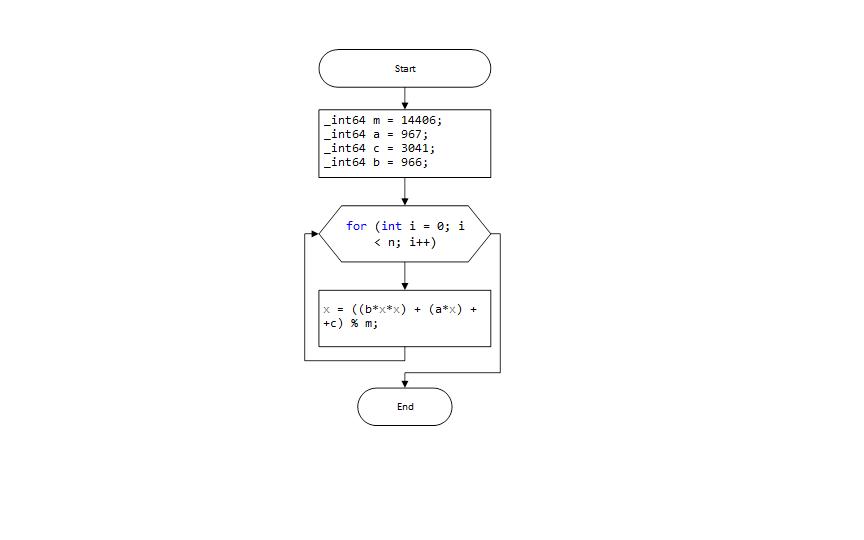
Реализация генератора на С++

intrandom2(_int64 &x)

{

_int64 m = 14406;

_int64 a = 967;

_int64 c = 3041;

_int64 b = 966;

x = ((b*x*x) + (a*x) + c) % m;

x = x % 100;

while (x> 9) x = x % 10;

returnx;

}

Вывод

Были разработаны генераторы равномерно распределенных случайных чисел на основе «Смешанного конгруэнтного метода» и «Квадратного конгруэнтного метода». Были сформированы по 30 последовательностей, с помощью разработанных генераторов, встроенной в Visual Stuido функции rand(), и встроенной в Pascal функции randomize.

---

Проверка генератора равномерно распределенных случайных чисел методом «Проверка частот»

Цель работы

Целью работы является тестирование генератора равномерно распределенных случайных чисел методом «Проверка частот».

Ход работы

В этом тесте для каждого целого значения 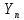подсчитывается их количество в последовательности, для чего используется одномерный массив 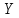размерностью 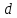. В заключение к этим числам в массиве 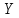применяется 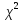- критерий с числом категорий, равным 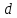. Вероятности попадания в каждую из категорий одинаковы и равны 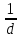.По результатам испытаний рассчитаем величину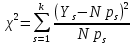





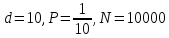
Выполним расчеты, и заполним таблицу.
Таблица квантилей для числа степеней свободы равное десяти.

Квантили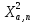
99	95	75	25	5	1
2.08790	3.32511	5.89883	11.38875	16.91898	21.66599

№ теста	Смешанный конгруэнтный	Квадратный конгруэнтный	C++	Pascal
1	4.94 (сл. подоз.)	9.36(удовл.)	9.40(удовл.)	10.62(удовл.)
2	5.44(сл. подоз.)	5.22(сл. подоз.)	7.16(удовл.)	8.42(удовл.)
3	7.36(удовл.)	9.84(удовл.)	8.46(удовл.)	12.34(сл. подоз.)
4	17.04 (сл. подоз.)	2.58(подозрит.)	6.04(удовл.)	3.56(сл. подоз.)
5	3.82(сл. подоз.)	22.02(неудовл.)	11.56(сл. подоз.)	13.06(сл. подоз.)
6	9.96(удовл.)	4.16(сл. подоз.)	3.58(сл. подоз.)	4.46(сл. подоз.)
7	5.18(сл. подоз.)	8.7(удовл.)	5.59(сл. подоз.)	6.22(удовл.)
8	7.70(удовл.)	1.84(неудовл.)	11.40(сл. подоз.)	13.04(сл. подоз.)
9	8.20(удовл.)	14.56(сл. подоз.)	3.84(сл. подоз.)	7.5(удовл.)
10	11.79(сл. подоз.)	4.64(сл. подоз.)	1.62(подозрит.)	8.98(удовл.)
11	4.26(сл. подоз.)	7.08(удовл.)	5.12(сл. подоз.)	16.62(сл. подоз.)
12	9.40(удовл.)	8.42(удовл.)	9.12(удовл.)	10.14(удовл.)
13	4.80(сл. подоз.)	11.46(сл. подоз.)	13.32(сл. подоз.)	13.54(сл. подоз.)
14	8.40(удовл.)	6.12(удовл.)	8.28(удовл.)	12.16(сл. подоз.)
15	13.88(сл. подоз.)	5.08(сл. подоз.)	4.36(сл. подоз.)	11.1(удовл.)
16	11.07(удовл.)	15.82(сл. подоз.)	18.07(подозрит.)	8.58(удовл.)
17	11.72(сл. подоз.)	5.5(сл. подоз.)	13.18(сл. подоз.)	5.34(сл. подоз.)
18	14.88(сл. подоз.)	6.68(удовл.)	13.58(сл. подоз.)	7.56(удовл.)
19	5.00(сл. подоз.)	7.14(удовл.)	11.42(сл. подоз.)	12.9(сл. подоз.)
20	5.78(сл. подоз.)	5(сл. подоз.)	3.86(сл. подоз.)	6.46(удовл.)
21	5.72(сл. подоз.)	12.78(сл. подоз.)	15.70(сл. подоз.)	8.58(удовл.)
22	8.37(удовл.)	11.76(сл. подоз.)	7.30(удовл.)	7.24(удовл.)
23	13.66(сл. подоз.)	3.32(подозрит.)	5.06(сл. подоз.)	10.82(удовл.)
24	5.58(сл. подоз.)	9.12(удовл.)	10.54(удовл.)	4.8(сл. подоз.)
25	12.17(сл. подоз.)	2.5(подозрит.)	9.22(удовл.)	10.92(удовл.)
26	15.04(сл. подоз.)	9.92(удовл.)	11.540(сл. подоз.)	10.16(удовл.)
27	6.26(удовл.)	7.44(удовл.)	15.28(сл. подоз.)	10(удовл.)
28	9.36(удовл.)	11.28(удовл.)	18.46(подозрит.)	9.14(удовл.)
29	3.96(сл. подоз.)	8.92(удовл.)	4.16(сл. подоз.)	8.9(удовл.)
30	16.68(сл. подоз.)	2.84(подозрит.)	8.70(удовл.)	8.26(удовл.)

---