Файл: Отчет по лабораторной работе по физике студент Группа Факультет Преподаватель Барнаул 2022.docx
Добавлен: 17.10.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Алтайский государственный технический университет им. И.И. Ползунова
Кафедра физики
ОТЧЕТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ ПО ФИЗИКЕ
Студент
Группа Факультет
Преподаватель
Барнаул – 2022
Номер варианта и данные к расчету
Лабораторная работа №3
Таблица 1.
-
№
варианта
расстояние R, см
Высота (расстояние), которое проходит груз
h, м
время движения груза
№
t1, c
t2, c
t3, c
4
14
24
10
1,1
1
6,38
6,41
6,45
2
4,29
4,31
4,33
3
3,49
3,53
3,52
4
2,93
2,92
2,95
Таблица 2.
-
№
варианта
Масса m, г
Высота (расстояние), которое проходит груз
h, м
время движения груза
№
t1, c
t2, c
t3, c
4
14
24
100
1,1
1
3,72
3,68
3,71
2
4,05
3,99
3,97
3
4,89
4,93
4,91
4
5,73
5,69
5,72
ОПИСАНИЕ УСТАНОВКИ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Д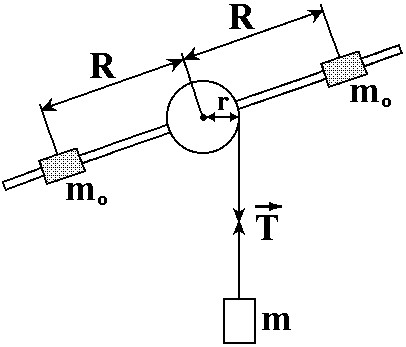 ля проверки основного закона динамики вращательного движения используется установка (рис. 3), называемая маятником Обербека. Она представляет собой шкив с приваренными к нему спицами. На спицах могут перемещаться два груза массой m0 = 53 г каждый, которые
ля проверки основного закона динамики вращательного движения используется установка (рис. 3), называемая маятником Обербека. Она представляет собой шкив с приваренными к нему спицами. На спицах могут перемещаться два груза массой m0 = 53 г каждый, которые
закрепляются специальными винтами
на расстоянии R от оси вращения. На
-
шкиве радиуса r намотана прочная
нить, к которой прикреплен груз массой m. При свободном опускании груза маятник вращается с постоянным ускорением.
Рис. 3. Схема экспериментальной установки машины Обербека.
Поскольку ось вращения для маятника Обербека закреплена, то соотношение (1) можно рассматривать в скалярном виде
М

I .
(7)
Чтобы установить справедливость соотношения (7), необходимо установить справедливость двух зависимостей
-
M
1

I
при
при
I const
M const,
и
что эквивалентно
1
 I
I
(8
Обозначим через I0 момент инерции маятника без грузов относительно оси вращения, а через Т силу натяжения нити. Тогда результирующий момент инерции маятника окажется равным
I = Iο + 2mο R2, (9)
где 2mοR2 – момент инерции грузов, находящихся на расстоянии R от оси
вращения.
Результирующий момент сил равен
M = Tr Mтр , (10)
где Mтр момент сил трения, возникающий между осью и шкивом, который для
каждой установки постоянен. Составим систему уравнений движения маятника и опускающегося груза
ITr M тр
ma mg T , (11)
где а ускорение опускающегося груза.
Умножим второе уравнение системы (11) на радиус шкива r и сложим с первым.
При этом следует учесть, что a r . Тогда (I mr 2)mgr M тр , с учетом формулы (9), получим:
(mgr Mтр)

(Iо o 2 mr2) . (12) 2m R
Так как при проверке первой зависимости (8) момент инерции системы не изменяется и в соотношении (12) знаменатель остается постоянным, то можно ввести следующие обозначения в выражении (12):
I1 = Iο + 2mοR2 + mr2, o Mтр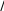 I1 некоторые постоянные.
I1 некоторые постоянные.
1
 mgr o при mgr Mтр
mgr o при mgr Mтр
I1
0 при mgr Mтр .
Тогда
(13)
Здесь момент силы тяжести груза mgr выступает в качестве аргумента. Установим R равным его среднему значению 10 см. Масса m может быть набрана из трех грузов одного основного 50 г (платформы) и двух дополнительных 50 г и 100 г. Диаметр шкива равен 20 мм, но при наматывании нити конечный диаметр составляет 24 мм. Поэтому можно принять эффективный диаметр шкива равным 22 мм, а эффективный радиус r=11 мм. Ускорение опускающегося груза может быть 2h

a t 2 . Тогда с учетом выражения a r угловое ускорение найдено, как
1 2 3 4 5
Алтайский государственный технический университет им. И.И. Ползунова
Кафедра физики
ОТЧЕТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ ПО ФИЗИКЕ
Студент
Группа Факультет
Преподаватель
Барнаул – 2022
Номер варианта и данные к расчету
Лабораторная работа №3
Таблица 1.
-
№
варианта
расстояние R, см
Высота (расстояние), которое проходит груз
h, м
время движения груза
№
t1, c
t2, c
t3, c
4
14
24
10
1,1
1
6,38
6,41
6,45
2
4,29
4,31
4,33
3
3,49
3,53
3,52
4
2,93
2,92
2,95
Таблица 2.
-
№
варианта
Масса m, г
Высота (расстояние), которое проходит груз
h, м
время движения груза
№
t1, c
t2, c
t3, c
4
14
24
100
1,1
1
3,72
3,68
3,71
2
4,05
3,99
3,97
3
4,89
4,93
4,91
4
5,73
5,69
5,72
ОПИСАНИЕ УСТАНОВКИ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Д ля проверки основного закона динамики вращательного движения используется установка (рис. 3), называемая маятником Обербека. Она представляет собой шкив с приваренными к нему спицами. На спицах могут перемещаться два груза массой m0 = 53 г каждый, которые
ля проверки основного закона динамики вращательного движения используется установка (рис. 3), называемая маятником Обербека. Она представляет собой шкив с приваренными к нему спицами. На спицах могут перемещаться два груза массой m0 = 53 г каждый, которые
закрепляются специальными винтами
на расстоянии R от оси вращения. На
-
шкиве радиуса r намотана прочная
нить, к которой прикреплен груз массой m. При свободном опускании груза маятник вращается с постоянным ускорением.
Рис. 3. Схема экспериментальной установки машины Обербека.
Поскольку ось вращения для маятника Обербека закреплена, то соотношение (1) можно рассматривать в скалярном виде
М

I .
(7)
Чтобы установить справедливость соотношения (7), необходимо установить справедливость двух зависимостей
-
M
1

I
при
при
I const
M const,
и
что эквивалентно
1
 I
I
(8
Обозначим через I0 момент инерции маятника без грузов относительно оси вращения, а через Т силу натяжения нити. Тогда результирующий момент инерции маятника окажется равным
I = Iο + 2mο R2, (9)
где 2mοR2 – момент инерции грузов, находящихся на расстоянии R от оси
вращения.
Результирующий момент сил равен
M = Tr Mтр , (10)
где Mтр момент сил трения, возникающий между осью и шкивом, который для
каждой установки постоянен. Составим систему уравнений движения маятника и опускающегося груза
ITr M тр
ma mg T , (11)
где а ускорение опускающегося груза.
Умножим второе уравнение системы (11) на радиус шкива r и сложим с первым.
При этом следует учесть, что a r . Тогда (I mr 2)mgr M тр , с учетом формулы (9), получим:
(mgr Mтр)

(Iо o 2 mr2) . (12) 2m R
Так как при проверке первой зависимости (8) момент инерции системы не изменяется и в соотношении (12) знаменатель остается постоянным, то можно ввести следующие обозначения в выражении (12):
I1 = Iο + 2mοR2 + mr2, o Mтр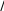 I1 некоторые постоянные.
I1 некоторые постоянные.
1
 mgr o при mgr Mтр
mgr o при mgr Mтр
I1
0 при mgr Mтр .
Тогда
(13)
Здесь момент силы тяжести груза mgr выступает в качестве аргумента. Установим R равным его среднему значению 10 см. Масса m может быть набрана из трех грузов одного основного 50 г (платформы) и двух дополнительных 50 г и 100 г. Диаметр шкива равен 20 мм, но при наматывании нити конечный диаметр составляет 24 мм. Поэтому можно принять эффективный диаметр шкива равным 22 мм, а эффективный радиус r=11 мм. Ускорение опускающегося груза может быть 2h

a t 2 . Тогда с учетом выражения a r угловое ускорение найдено, как
1 2 3 4 5
-
№
варианта
расстояние R, см
Высота (расстояние), которое проходит груз
h, м
время движения груза
№
t1, c
t2, c
t3, c
4
14
24
10
1,1
1
6,38
6,41
6,45
2
4,29
4,31
4,33
3
3,49
3,53
3,52
4
2,93
2,92
2,95
-
№
варианта
Масса m, г
Высота (расстояние), которое проходит груз
h, м
время движения груза
№
t1, c
t2, c
t3, c
4
14
24
100
1,1
1
3,72
3,68
3,71
2
4,05
3,99
3,97
3
4,89
4,93
4,91
4
5,73
5,69
5,72
-
шкиве радиуса r намотана прочная
нить, к которой прикреплен груз массой m. При свободном опускании груза маятник вращается с постоянным ускорением.
Рис. 3. Схема экспериментальной установки машины Обербека.
-
M
1

I
при
при
I const
M const,
и
что эквивалентно
1  I
I
2h

rt 2 .
определится как
(14)
Изменение массы груза m производится в соответствии с таблицей 1 исходных данных, в которую так же вносятся результаты измерений и расчетов.
Таблица 1
-
№ изм.
m, г
mgr∙10-2,
Нм
t1 , c
t2 , c
t3 , c
tср , c
,
рад/с2
, рад/с2
Относит. погрешность,
%
1
50
0,55
6,38
6,41
6,45
6,41
31,2
3,9
12,5
2
50+50=100
1,10
4,29
4,31
4,33
4,31
46,4
5,66
12,2
3
50+100=150
1,65
3,49
3,53
3,52
3,51
56,98
7,19
12,6
4
50+100+50=200
2,20
2,93
2,92
2,95
2,93
68,26
8,81
12,9
Данные установки: h = 1,1 м; R = 10 см; r = 11 мм
. tсист = 0,01 с ;hcист = 0,005 м.
По данным таблицы 1 строится график зависимости углового ускорения от момента силы тяжести опускающегося груза mgr, т.е. ε=f(mgr). Отрезок, отсекаемый прямой на оси моментов сил
, равен моменту сил трения, возникающему при трении шкива об ось.
Проверка второй зависимости (8) осуществляется путем выполнения второй серии опытов. Для этого перепишем соотношение (12) в виде

1 2m Ro 2 Io mr2
mgr Mтр mgr Mтр . (15)
При постоянной массе m груза второе слагаемое, а также знаменатель первого слагаемого в выражении (15) остаются постоянными. Таким образом, величина 1/ должна быть пропорциональна изменяющемуся моменту инерции грузов 2mοR2.
1 rt 2

Величину 1/ находят в соответствие с (14) по формуле: 2h .
Массу груза m на нити установить равной 100 г (или 50 г). Момент инерции грузов меняется за счет изменения расстояния R грузов m0 до оси вращения в соответствии с таблицей 2, в которую так же вносятся результаты измерений и расчетов. Воспользовавшись данными своего варианта заполнить таблицу 2.
Таблица 2
-
№ изм.
R, см
2mοR2 ∙10-3, кгм2
t1 , c
t2 , c
t3 , c
tср , c
-1 ,
с2/рад
-1 ,
с2/рад
Относит. погрешность,
%
1
5
0,265
3,72
3,68
3,71
3,70
0,019
0,0024
12,6
2
10
1,06
4,05
3,99
3,97
4
0,02
0,0025
12,5
3
15
2,39
4,89
4,93
4,91
4,91
0,025
0,0038
15,2
4
19
3,83
5,73
5,69
5,72
5,71
0,029
0,0034
11,7
Данные установки: h = 1,1 м; m = 100 г; mgr = 0,011 Нм .
По данным таблицы 2 строится график зависимости 1/ от переменного момента инерции 1/ε=f(2mοR2). Отрезок, отсекаемый графиком на оси моментов инерции, равен моменту инерции маятника без грузов m0 , то есть моменту инерции шкива и спиц.
По данным приборов определяют систематические погрешности tсист и hcист. Поскольку высота, с которой опускается груз каждый раз задается одинаковым образом, то можно считать, что hсл=0. Случайная погрешность в определении времени находится обычным образом по трем измерениям.
Полная погрешность находится по формуле t =tcист+tсл. Погрешность r можно положить равной 1 мм. Погрешности в определении углового ускорения рассчитываются по формулам:
h r t
 2
2 h r tср
. (16)
1 1 h r t

h r 2 tср
Выражение, стоящее в квадратных скобках, следует рассчитать один раз для средней строки одной из таблиц и использовать это значение для расчета погрешностей и -1 в каждой строке таблиц 1 и 2. По результатам работы сделать соответствующие выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Записать и объяснить основной закон динамики вращательного движения. Дать определения величин, входящих в это уравнение. -
Как определяется направление углового ускорения и момента сил? -
Какой физический смысл имеет отрезок, отсекаемый прямой на оси абсцисс на графике ε=f(mgr)? -
Какой физический смысл имеет отрезок, отсекаемый прямой на оси абсцисс на графике 1/ε=f(2mοR2)?
О.l = r∙sinα
-
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения
параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление
вектора углового ускорения совпадает с направлением вектора угловой скорости. А если величина угловой
скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой
скорости.
Момент силы является векторной величиной, направление которой определяется по правилу правой руки.
Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы,
то вытянутый большой палец укажет направление вектора момента силы.
-
Угловое ускорение прямо пропорционально моменту сил. -
Угловое ускорение обратно пропорционально моменту инерции.
ВЫЧИСЛЕНИЯ:


tср = (t1+t2+t3)/3
tср1 = (6,38+6,41+6,45)/3=6,41 tср1 = (3,72+3,68+3,71)/3=3,70
tср2 = (4,29+4,31+4,33)/3=4,31 tср2 = (4,05+3,99+3,97)/3=4
tср3 = (3,49+3,53+3,52)/3=3,51 tср3 = (4,89+4,93+4,91)/3=4,91
tср4 = (2,93+2,92+2,95)/3=2,93 tср4 = (5,73+5,69+5,72)/3=5,71

