Файл: готовая записка-2.docx

3.2 Синтез и анализ планетарного редуктора

Исходные данные:

Частота вращения двигателя n_дв=5000 мин^-1;

Частота вращения кривошипа n_кр=250 мин^-1;

Число зубьев шестерни z₅=11;

Число зубьев колеса z₆=22;

Модуль планетарного редуктора m=8 мм.

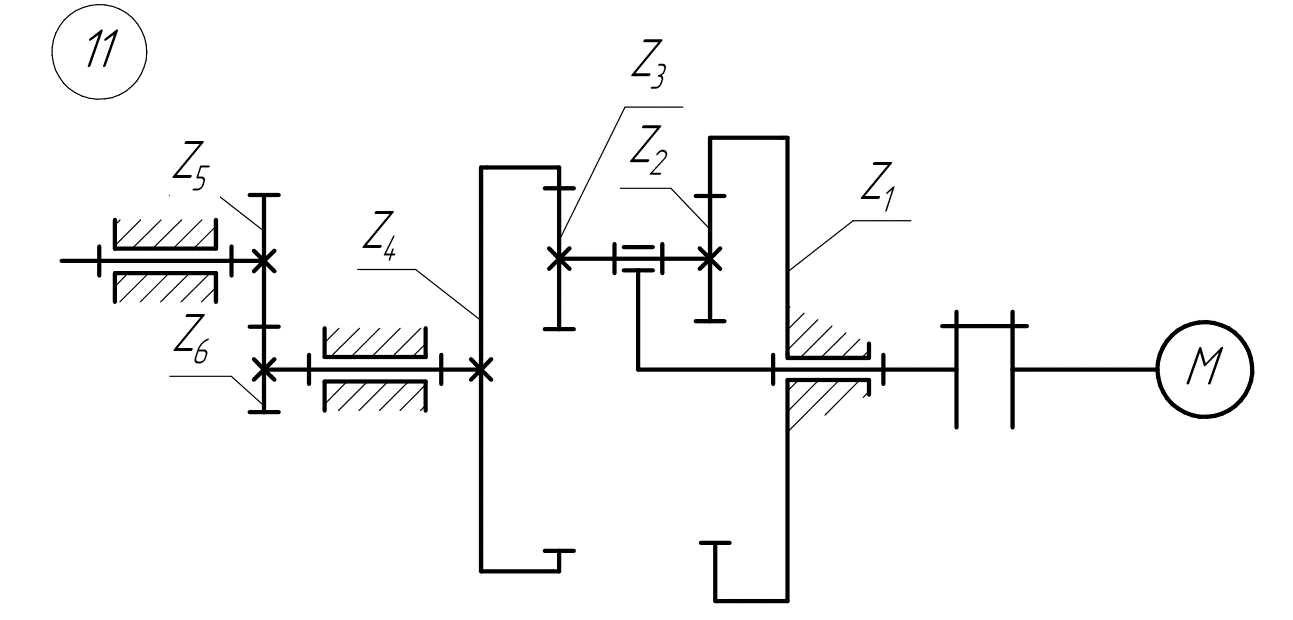
Рисунок 3.1 - Схема планетарного редуктора

Общее передаточное отношение редуктора:

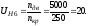
Передаточное отношение простой передачи z₅-z₆:

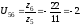
Передаточное отношение планетарной передачи:

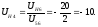
Передаточное отношение обращённого планетарного механизма – простого зубчатого ряда:

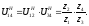
Формула Виллиса. Передаточное отношение обращённого механизма:

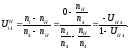
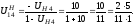
Условие соосности для данной передачи:

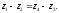
Принимаем числа зубьев колёс, равными: z₁=88; z₂=16; z₃=18; z₄=90.

Диаметры колёс:

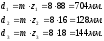
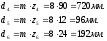
Принимаем масштабный коэффициент построения кинематической схемы редуктора:

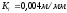
Скорость точки А зубчатого колеса 1:

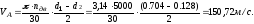
Строим планы скоростей. Масштабный коэффициент плана скоростей:

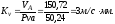
Строим план частот редуктора. Масштабный коэффициент плана частот вращения редуктора:

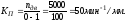
3.3 Определение частот вращения зубчатых колес аналитическим и графическим методами

Значения частот, полученных графическим методом:

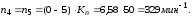
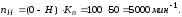
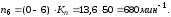
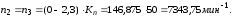
Значения частот, полученные аналитическим методом:

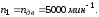
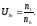
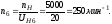
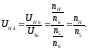
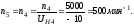
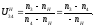
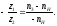
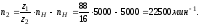
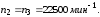
Определяем погрешность расчётов:

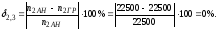
4 Синтез и анализ кулачкового механизма

Исходные данные:

а) диаграмма движения выходного звена

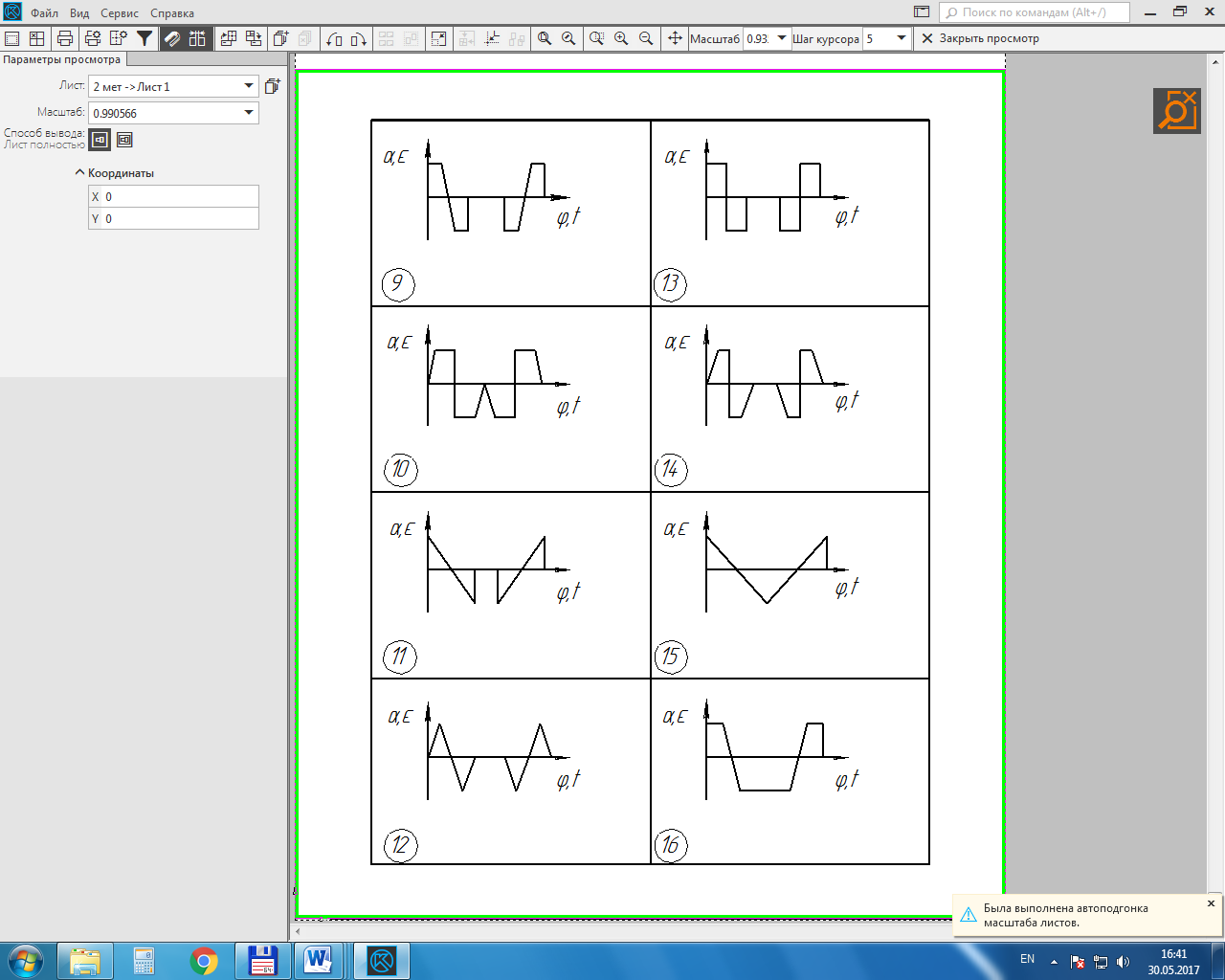
б) частота вращения кулачкаn_кул=250 мин^-1;

в) ход толкателя h=8мм;

г) рабочий угол кулачка φ_р=126 град;

д) кулачковый механизм с плоским толкателем

4.1 Построение кинематических диаграмм и определение масштабных коэффициентов

По заданному графику ускорения толкателя a = f(t), графическим интегрированием по методу хорд получаю графики скорости и перемещения толкателя (обратным интегрированием).Графики a = f(v), a = f(s), v = f(s) получаем методом исключения общего переменного.

База интегрирования:

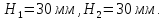
Масштабный коэффициент перемещения толкателя:

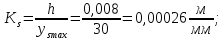
гдеy_smax–максимальное значение ординаты графикаs=f(t), мм.

Масштабный коэффициент времени:

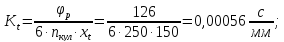
гдеn_кул– частота вращения кулачка:

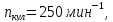
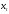=150 мм – длина отрезка на оси абсцисс графика, изображающая время поворота кулачка на рабочий угол.

Масштабный коэффициент скорости толкателя:

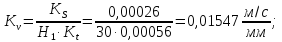
Масштабный коэффициент ускорения толкателя:

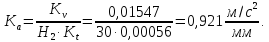
4.2 Определение минимального радиуса кулачка

Принимаю масштабный коэффициент построения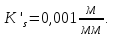

Значение минимального радиуса центрового профиля кулачка:

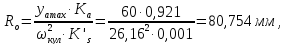
где y_amax – максимальное значение ординаты графика a = f(t), мм,

ω_кул – угловая скорость кулачка,

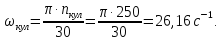
4.3 Построение профиля кулачка

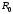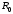Проводим из цента О₁ окружность минимального радиуса R_o. На окружности минимального радиуса , в обращенном движении, откладываем рабочий угол и делим его на равные части, как и ось t графика s = f(t).Через точки 0, 1, 2.., 12, к центру O₁проводим лучи, на которых от окружности радиуса откладываем перемещенияy’_S0, y’_S1,y’_S2,…y’_S12.Через эти точки проводим перпендикуляры в лучах, т.е. положение тарелки толкателя в обращенном движении. Действительным профилем будет огибающая всех положений тарелки, т.е. необходимо построить плавную кривую, касающуюся перпендикуляров в каждом положении.

В одном из положений изображаем толкатель и все кинематические пары, образованные подвижными звеньями между собой и со стойкой.

4.4 Определение максимальной линейной скорости и ускорения толкателя

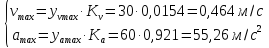
Заключение

Курсовое проектирование способствует комплексному решению задач по исследованию, проектированию и расчету механизмов и машин.

В данном курсовом проекте были проведены синтез и анализ кулачковых, зубчатых механизмов, силовой анализ рычажных механизмов, разработка структурных схем механизма.

В основе синтеза и анализа зубчатого механизма были решены вопросы геометрического синтеза зубчатого зацепления (геометрия и кинематика зубчатой передачи). Были проведены расчёты геометрических параметров зубчатых передач и подбор чисел зубьев планетарного зубчатого механизма по заданному передаточному отношению и условию соосности, а также построение плана скоростей и частот вращения колёс механизма.

Список литературы

1 А. А. Машков, Теория механизмов и машин. – Машиностроение,

г. Москва, 1969г. – 583.

2 С. Н. Кожевников, Теория механизмов и машин. – Машиностроение,

г. Москва, 1969г. – 583с.

3 А. С. Кореняко, Курсовое проектирование по теории механизмов и

машин. – Высшая школа, Киев, 1970г. – 330с.

4 И. П. Филонов, Теория механизмов и машин и манипуляторов. –

Дизайн ПРО, г. Минск, 1998г. – 428с.

5 И. И. Артоболевский, Теория механизмов и машин. – Наука, г. Москва,

1998г. – 720с.

6 К. В. Фролов, Теория механизмов и машин. – Высшая школа, г. Москва,

1998г. – 494с.

Белорусско – Российский университет

гр. АВТ-161