ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 143
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=f (X, Z). Если X, Y, Z - real, то полное число тестов (232) 2 = 264×1031 Если на каждый тест тратить 1 мс, то 264 мс = 800 млн. лет. Следовательно:
· в любой нетривиальной программе на любой стадии ее готовности содержатся необнаруженные ошибки;
· тестирование - технико-экономическая проблема, основанная на компромиссе время - полнота. Поэтому нужно стремиться к возможно меньшему количеству хороших тестов с желательными свойствами.
Детективностъ: тест должен с большой вероятностью обнаруживать возможные ошибки
Покрывающая способность: один тест должен выявлять как можно больше ошибок.
Воспроизводимость: ошибка должна выявляться независимо от изменяющихся условий (например, от временных соотношений) - это труднодостижимо для времязависимых программ, результаты которых часто невоспроизводимы.
Только на основании выбранного критерия можно определить тот момент времени, когда конечное множество тестов окажется достаточным для проверки программы с некоторой полнотой (степень полноты, впрочем, определяется экспериментально). Используется два вида критериев (табл.2):
· функциональные тесты составляются исходя из спецификации программы;
· структурные тесты составляются исходя из текста программы.
Виды критериев и их функциональность
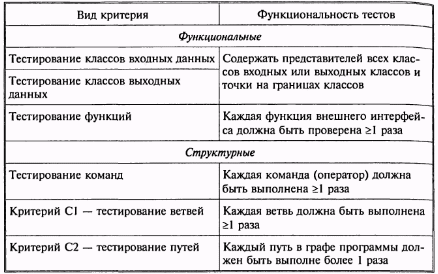
На рис.1, а видно отличие тестирования команд (достаточен один тест) от С1 (необходимы два теста как минимум). Рисунок 1, б иллюстрирует различие С1 (достаточно двух тестов, покрывающих пути 1, 4 или 2,3) от С2 (необходимо четыре теста для всех четырех путей). С2 недостижим в реальных программах из-за их цикличности, поэтому ограничиваются тремя путями для каждого цикла: 0, 1 и N повторений цикла.
Остаются проблемы назначения классов входных/выходных данных для функционального тестирования и проектирования тестов для структурного тестирования. Классы, как правило, назначаются исходя из семантики решаемой задачи. [2]
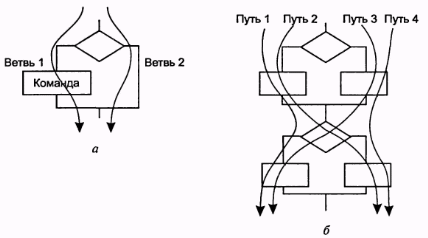
Траектории вычислений при структурном тестировании
Если разработчик предполагает, что программой будут пользоваться другие, то он обязательно должен создать справочную систему и обеспечить пользователю удобный доступ к справочной информации во время работы с программой. В современных программах справочная информация представляется в форме СНМ - или HLP-файлов. Помимо справочной информации, доступ к которой осуществляется из программы во время ее работы, в состав справочной системы включают инструкцию по установке (инсталляции) программы, которую оформляют в виде Readme-файла в одном из форматов: TXT, DOC или НТМ.
Установочный диск или CD-ROM создаются для того, чтобы пользователь мог самостоятельно, без помощи разработчика, установить программу на свой компьютер. Обычно помимо самой программы на установочном диске находятся файлы справочной информации и инструкция по установке программы (Readme-файл). Следует понимать, что современные программы, в том числе разработанные в Borland C++, в большинстве случаев (за исключением самых простых программ) не могут быть установлены на компьютер пользователя путем простого копирования, так как для своей работы требуют специальных библиотек и компонентов, которых может и не быть у конкретного пользователя. Поэтому установку программы на компьютер пользователя должна выполнять специальная программа, которая помещается на установочный диск. Как правило, установочная программа создает отдельную папку для устанавливаемой программы, копирует в нее необходимые файлы и, если надо, выполняет настройку операционной системы путем внесения дополнений и изменений в реестр. [2]
Традиционную теорию (обычных) множеств можно рассматривать как частный случай теории нечетких подмножеств (почему нужно говорить "нечеткое подмножество" а не "нечеткое множество", понятно хотя бы из того, что область определения нечеткого подмножества - всегда обычное, а не нечеткое множество). Важно, что здесь мы имеем новое и очень полезное для нас расширение традиционного понятия. И тем не менее, все то, что можно описать или объяснить с помощью теории нечетких подмножеств, рассматривают и без этой теории, используя другие понятия. Всегда можно зеленить одно математическое понятие другим. Но будет ли это новое понятие настолько же понятным, как и старое, и будет ли оно порождать свойства, которые с его помощью было бы легче обнаружить, доказать и использовать
Пусть Е есть множество, А - подмножество Е: А Ì Е.
Тот факт, что элемент х множества Е есть элемент подмножества А, или, как еще говорят, принадлежит А, обычно обозначают с помощью символа Î:х Î А
Для выражения этой принадлежности можно использовать и другое понятие - характеристическую функцию mА (х), значения которой указывают, является ли (да или нет) х элементом А:

Напомним хорошо известные свойства булевой бинарной алгебры. Пусть А - дополнение А относительно Е, т.е. такое подмножество Е, для которого АÇА=Æ, АÈА=Е. Если хÎА, то хÏА, и можно записать mА (х) = 1, mА (х) = 0.
Для двух данных подмножеств А и В можно рассмотреть пересечение А Ç В.
Имеем



Это позволяет нам записать
mАÇВ (х) = mА (х) * mВ (х)
где операция * определена таблицей на рис.2 и называется булевым произведением.
Таким же образом для двух подмножеств А и В определяют объединение или соединение

обладающее свойством
mАÈВ (х) = mА (х) mВ (х)
mВ (х)
где операция (булева сумма) определена таблицей на рис.3.
(булева сумма) определена таблицей на рис.3.

Дадим строгое определение понятия, нечеткого подмножества, введенного Заде.
Пусть Е есть множество, счетное или нет, их - элемент Е. Тогда нечетким подмножеством А множества Е называется множество упорядоченных пар
{ (x|mA (x)) }, " x Î E
где mA (x) - степень принадлежности x в А. Таким образом, если mA (x) принимает свои значения во множестве М значений функции принадлежности или, короче, во множестве принадлежностей, то можно сказать, что х принимает значение в М посредством функции
· в любой нетривиальной программе на любой стадии ее готовности содержатся необнаруженные ошибки;
· тестирование - технико-экономическая проблема, основанная на компромиссе время - полнота. Поэтому нужно стремиться к возможно меньшему количеству хороших тестов с желательными свойствами.
Детективностъ: тест должен с большой вероятностью обнаруживать возможные ошибки
Покрывающая способность: один тест должен выявлять как можно больше ошибок.
Воспроизводимость: ошибка должна выявляться независимо от изменяющихся условий (например, от временных соотношений) - это труднодостижимо для времязависимых программ, результаты которых часто невоспроизводимы.
Только на основании выбранного критерия можно определить тот момент времени, когда конечное множество тестов окажется достаточным для проверки программы с некоторой полнотой (степень полноты, впрочем, определяется экспериментально). Используется два вида критериев (табл.2):
· функциональные тесты составляются исходя из спецификации программы;
· структурные тесты составляются исходя из текста программы.
Виды критериев и их функциональность

На рис.1, а видно отличие тестирования команд (достаточен один тест) от С1 (необходимы два теста как минимум). Рисунок 1, б иллюстрирует различие С1 (достаточно двух тестов, покрывающих пути 1, 4 или 2,3) от С2 (необходимо четыре теста для всех четырех путей). С2 недостижим в реальных программах из-за их цикличности, поэтому ограничиваются тремя путями для каждого цикла: 0, 1 и N повторений цикла.
Остаются проблемы назначения классов входных/выходных данных для функционального тестирования и проектирования тестов для структурного тестирования. Классы, как правило, назначаются исходя из семантики решаемой задачи. [2]

Траектории вычислений при структурном тестировании
Создание справочной системы
Если разработчик предполагает, что программой будут пользоваться другие, то он обязательно должен создать справочную систему и обеспечить пользователю удобный доступ к справочной информации во время работы с программой. В современных программах справочная информация представляется в форме СНМ - или HLP-файлов. Помимо справочной информации, доступ к которой осуществляется из программы во время ее работы, в состав справочной системы включают инструкцию по установке (инсталляции) программы, которую оформляют в виде Readme-файла в одном из форматов: TXT, DOC или НТМ.
Создание установочного диска
Установочный диск или CD-ROM создаются для того, чтобы пользователь мог самостоятельно, без помощи разработчика, установить программу на свой компьютер. Обычно помимо самой программы на установочном диске находятся файлы справочной информации и инструкция по установке программы (Readme-файл). Следует понимать, что современные программы, в том числе разработанные в Borland C++, в большинстве случаев (за исключением самых простых программ) не могут быть установлены на компьютер пользователя путем простого копирования, так как для своей работы требуют специальных библиотек и компонентов, которых может и не быть у конкретного пользователя. Поэтому установку программы на компьютер пользователя должна выполнять специальная программа, которая помещается на установочный диск. Как правило, установочная программа создает отдельную папку для устанавливаемой программы, копирует в нее необходимые файлы и, если надо, выполняет настройку операционной системы путем внесения дополнений и изменений в реестр. [2]
2. Математическая часть
Традиционную теорию (обычных) множеств можно рассматривать как частный случай теории нечетких подмножеств (почему нужно говорить "нечеткое подмножество" а не "нечеткое множество", понятно хотя бы из того, что область определения нечеткого подмножества - всегда обычное, а не нечеткое множество). Важно, что здесь мы имеем новое и очень полезное для нас расширение традиционного понятия. И тем не менее, все то, что можно описать или объяснить с помощью теории нечетких подмножеств, рассматривают и без этой теории, используя другие понятия. Всегда можно зеленить одно математическое понятие другим. Но будет ли это новое понятие настолько же понятным, как и старое, и будет ли оно порождать свойства, которые с его помощью было бы легче обнаружить, доказать и использовать
Пусть Е есть множество, А - подмножество Е: А Ì Е.
Тот факт, что элемент х множества Е есть элемент подмножества А, или, как еще говорят, принадлежит А, обычно обозначают с помощью символа Î:х Î А
Для выражения этой принадлежности можно использовать и другое понятие - характеристическую функцию mА (х), значения которой указывают, является ли (да или нет) х элементом А:

Напомним хорошо известные свойства булевой бинарной алгебры. Пусть А - дополнение А относительно Е, т.е. такое подмножество Е, для которого АÇА=Æ, АÈА=Е. Если хÎА, то хÏА, и можно записать mА (х) = 1, mА (х) = 0.
Для двух данных подмножеств А и В можно рассмотреть пересечение А Ç В.
Имеем



Это позволяет нам записать
mАÇВ (х) = mА (х) * mВ (х)
где операция * определена таблицей на рис.2 и называется булевым произведением.
Таким же образом для двух подмножеств А и В определяют объединение или соединение

обладающее свойством
mАÈВ (х) = mА (х)
где операция

Дадим строгое определение понятия, нечеткого подмножества, введенного Заде.
Пусть Е есть множество, счетное или нет, их - элемент Е. Тогда нечетким подмножеством А множества Е называется множество упорядоченных пар
{ (x|mA (x)) }, " x Î E
где mA (x) - степень принадлежности x в А. Таким образом, если mA (x) принимает свои значения во множестве М значений функции принадлежности или, короче, во множестве принадлежностей, то можно сказать, что х принимает значение в М посредством функции

