Файл: Перевод чисел из одной позиционной системы счисления в другую.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 91
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 2. Составьте таблицы истинности для следующих логических формул
1.
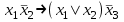 ;
;| X1 | X2 | X3 | 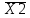 | X1 * 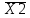 | X1+X2 | 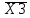 | (X1+X2)* 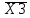 | X1 * 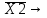 (X1+X2)* (X1+X2)* 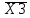 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
2.
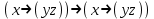
;
| XX | Y | Z | YZ | X 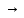 YZ YZ | (X 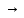 YZ) YZ)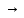 ( (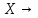 YZ) YZ) |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
3.
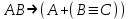 ;
;| A | B | C | AB | B≡C | A+(B≡C) | AB 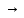 A+(B≡C) A+(B≡C) |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Задание 3: Какой логической функции соответствует таблица истинности?
| A | B | C | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
-
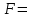 не
не 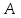 или
или 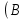 и
и  ;
; -
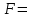
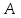 и
и 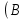 или
или  ;
; -
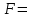 не
не 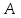 и
и 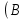 или
или  ;
; -
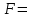 не
не 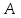 и
и 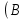 и
и  .
.
Задание 4: Применяя таблицы истинности, докажите тождественную истинность
логических формул:
1.
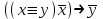 ;
;| X | Y | (X≡Y) | 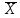 | ((X≡Y) 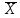 ) ) | 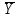 | ((X≡Y) 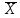 ) )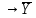 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
2.
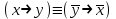 ;
;| X | Y | X  Y Y | 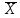 | 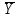 | 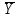  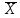 | (X  Y) ≡( Y) ≡(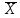  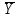 ) ) |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
3
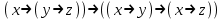 .
.| X | Y | Z | Y  Z Z | (X  (Y (Y Z)) Z)) | X  Y Y | X  Z Z | ((X  Y) Y) (X (X Z)) Z)) | (X  (Y (Y Z)) Z)) ((X ((X Y) Y) (X (X Z)) Z)) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |

