Файл: Перевод чисел из одной позиционной системы счисления в другую.docx

3. ;










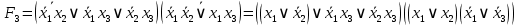
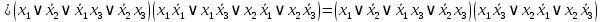
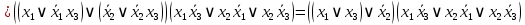
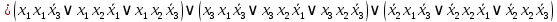
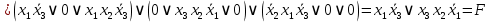
Для проверки эквивалентности построим таблицу истинности обоих функций и убедимся, что столбцы значений совпадают:

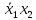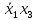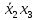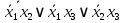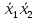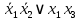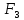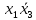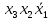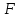0	0	0	0	0	0	1	1	0	1	0	0	0	0
0	0	1	0	1	1	1	1	0	1	0	0	0	0
0	1	0	1	0	0	0	0	0	0	0	0	0	0
0	1	1	1	1	0	1	0	0	0	1	0	1	1
1	0	0	0	0	0	1	0	0	0	1	1	0	1
1	0	1	0	0	1	1	0	1	1	0	0	0	0
1	1	0	0	0	0	1	0	0	0	1	1	0	1
1	1	1	0	0	0	1	0	1	1	0	0	0	0

---

4. ;








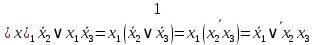
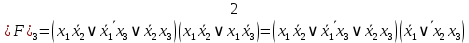
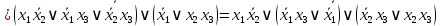
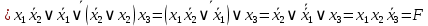
Для проверки эквивалентности построим таблицу истинности обоих функций и убедимся, что столбцы значений совпадают:

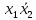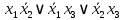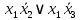0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	1	1	1	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0
0	1	1	0	1	0	1	0	0	0	0
1	0	0	1	0	0	1	1	1	0	0
1	0	1	1	0	1	1	0	1	0	0
1	1	0	0	0	0	0	1	1	1	1
1	1	1	0	0	0	0	0	0	0	0

---

---

Задание 9. Заданы две логические функци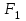и и 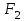. Путем тождественных преобразований получите минимальную форму записи функций и проверьте, является ли функция 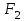тождественной функции .

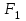1. 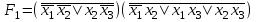; 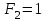на наборах 0, 4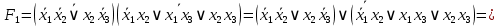






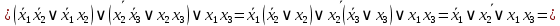
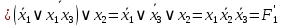
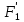является минимальной формой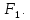

Упростим СДНФ функции :



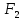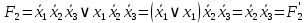
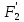является минимальной формой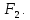

Заметим, что 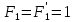только на наборе 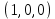(набор 4). Следовательно, не равна тождественно .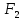
2. ;














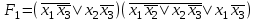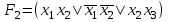
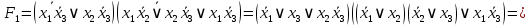
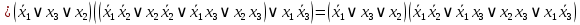
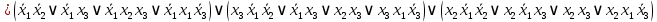
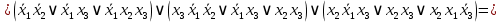
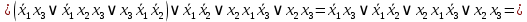
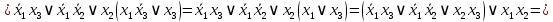
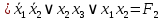
Следовательно,

---

равна тождественно .
3. 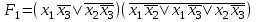; на наборах 0, 1, 3, 7






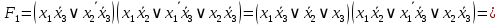
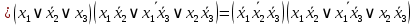
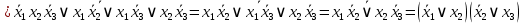
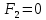на наборах 2, 4, 5, 6. Упрощаем СКНФ: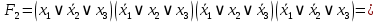







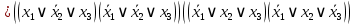
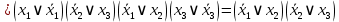
Следовательно, равна тождественно .

Задание 10. Найти формулу, определяющую функцию Ф(x,y,z), по заданной таблице истинности:

x	y	z	Ф(x,y,z)
1	1	1	1
1	1	0	0
1	0	1	0
1	0	0	0
0	1	1	1
0	1	0	1
0	0	1	1
0	0	0	1

Функция принимает ложное значение на наборах:

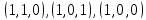
Им соответствуют следующие элементарные дизъюнкции:

---