Файл: Перевод чисел из одной позиционной системы счисления в другую.docx

Тогда совершенная конъюнктивная форма получается объединением этих дизъюнкций с помощью операции конъюнкции:
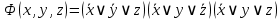
Задание 11. По таблицам истинности найдите формулы, определяющие функции

F1(x,y,z), F2(x,y,z), F3(x,y,z), F4(x,y,z) и придайте им более простой вид:

x	y	z	F1(x,y,z)	F2(x,y,z)	F3(x,y,z)	F4(x,y,z)
1	1	1	0	1	1	1
1	1	0	1	1	1	0
1	0	1	1	0	0	1
1	0	0	1	0	0	1
0	1	1	0	0	0	0
0	1	0	0	1	1	0
0	0	1	1	0	1	1
0	0	0	0	0	0	0

1. Функция принимает истинное значение на наборах: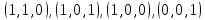

---

Им соответствуют следующие элементарные конъюнкции:

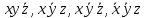
Тогда совершенная дизъюнктивная форма получается объединением этих конъюнкций с помощью операции дизъюнкции:



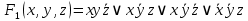
Упростим эту формулу



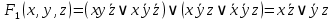
2. Функция принимает истинное значение на наборах:

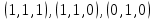
Им соответствуют следующие элементарные конъюнкции:

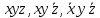
Тогда СДНФ равна: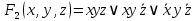



Упростим эту формулу



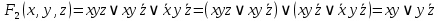
3. Функция принимает истинное значение на наборах:

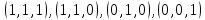
Им соответствуют следующие элементарные конъюнкции:

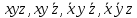
Тогда СДНФ равна: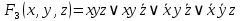



Упростим эту формулу



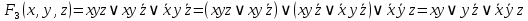
4. Функция 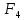принимает истинное значение на наборах: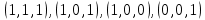

Им соответствуют следующие элементарные конъюнкции:

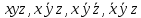
Тогда СДНФ 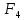равна: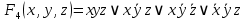



Упростим эту формулу


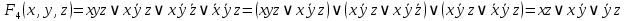
Задание 12. Докажите равносильность формул 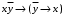и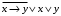

сравнением их совершенных нормальных форм (конъюнктивных или дизъюнктивных)

---

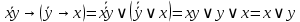
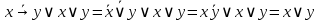
Так как совершенные конъюнктивные нормальный формы совпадают, то формулы и равносильны.
Задание 13. Определите корень Х = F(А,В) логического уравнения




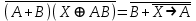
Пусть 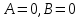. Тогда уравнение при данных и 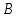преобразуется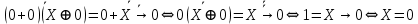



Пусть 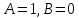. Тогда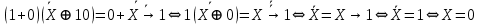



Пусть 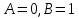. Тогда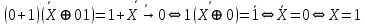



Пусть 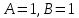. Тогда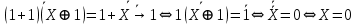



Следовательно, .

---
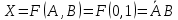