Файл: Перевод чисел из одной позиционной системы счисления в другую.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 86
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа № 1 по информатике
Тема: «Перевод чисел из одной позиционной системы счисления в другую»
Задание 1. Переведите десятичные числа в двоичную систему счисления:
1) 96 = 1100000 2) 0.114 = 0.000111 3) 34.675 = 100010. 10101100
4) 27 = 110011 5) 0.65 = 0.10100110 6) 0.25 = 0.01
Задание 2. Переведите десятичные числа в восьмеричную систему счисления:
1) 20 = 24 2) 0.44 = 0.341 3) 36.25 = 44.2
Задание 3. Переведите десятичные числа в шестнадцатеричную систему счисления:
1) 128 = 80 2) 100 = 64 3) 0.125 = 0.2 4) 345.75 = 159.C
Задание 4. Выполните перевод чисел, используя схему А2 А8 А16
1) 11111112 = 1778 = 7F16 2) 10110112 = 1338 = 5B16
3) 100002 = 234208 = 271016 4) 1100101110112 = 14738 = 33B16
Задание 5. Выполните перевод чисел, используя схему А16 А2 А8 А10
1) 10016 = 1000000002 = 4008 = 25610
2) 1016 = 100002 = 208 = 1610
3) АВС16 = 1010101111002 = 52748 = 274810
4) FF16 = 111111112 = 3778 = 25510
5) 56816 = 101011010002 = 25508 = 138410
6) AB16 = 101010112 = 2538 = 17110
Задание 6. Переведите восьмеричное число 0.3(52)8 в систему счисления по основанию 16.
Решение:
0.3(52)8 = 0,7(5)16
Задание 7. Переведите шестнадцатеричное число 0.6(9)16 в систему счисления по основанию 8.
Решение:
0.6(9)16 = 0.32(31)8
Задание 8. Переведите четверичное число 0.31(13)4 в систему счисления по основанию 8.
Решение:
0.31(13)4 = 0.6(56)8
Задание 9. Переведите шестнадцатеричное число 0.F(2)16 в систему счисления по основанию 8.
Решение:
0.F(2)16 = 0.74(4210)8
Задание 10. Даны три числа A, B и C, записанные соответственно в троичной, восьмеричной и шестнадцатеричной системах счисления:
A = 21121.223
B = 153.1468
C = 26B.CD16
Какова сумма этих чисел, записанная в двоичной системе счисления?
Решение:
A = 21121.223 = 205.8888888888910
B = 153.1468 = 107.1992187510
C = 26B.CD16 = 619.8007812510
205.8888888888910 + 107.1992187510 + 619.8007812510 = 932.8888888888910
932.8888888888910 = 1110100100.1110001110001110001110012
Контрольная работа № 2 по информатике
Тема: «Выполнение арифметических операций в различных позиционных системах счисления»
Задание 1. Определите десятичный эквивалент (А10) двоичного числа (А2).
1) 1001 = 9 2) 1111 = 15 3) 1011101=93
4) 100110 = 38 5) 1111111001 = 1017 6) 0.01 =0.25
Задание 2. Определите десятичный эквивалент (А10) восьмеричного числа (А8).
1) 100 = 64 2) 50 = 40 3) 102 = 66
4) 0.7 = 0.875 5) 0.04 = 0.0625 6) 0.36 = 0.46875
7) 76.05 =62.078125
Задание 3. Определите десятичный эквивалент (А10) шестнадцатеричного числа (А16)
1) 40 = 64 2) 41 = 65 3) АВС = 2748
4) FC = 252 5) 100 = 256 6) 0.08 = 0.3125
7) 0.АВ = 0.66796875 8) 54.0С = 84.046875
Задание 4. Определите сумму двоичных чисел (S=А+В). Проверьте результат путем перевода аргументов и суммы в десятичную систему счисления (А2А10, В2В10, S2S10)
1) 101+101 = 1010(1010) 2) 1001+1101 = 10110(2210)
(510+510=1010) (910+1310=2210)
3) 110+1011 =10001(1710) 4) 110110+111010 = 1110000(11210)
(610+1110=1710) (5410+5810=11210)
5) 10101.101+11.01 =11000.111 (24.87510)
(21.62510+3.2510=24.87510)
6) 10001.11+101.0011 = 10110.1111(22.937510)
(17.7510+5.187510=22.937510)
Задание 5. Выполните вычитание двоичных чисел с проверкой и использованием прямого и обратного кодов
1) 1101-101 = 1000
(11012+0102 = 1112 +12 = 10002
1310-510=810)
2) 1101-1001
(11012+01102 =112+12=1002
1310-910=410)
3) 111-1010
(1112+01012=11002=-112
710-1010=-310)
4) 100-10
(1002+0012=0012+12=102
410-210=210)
5) 1111-11111
(11112+1000002=1011112+12=-100002
1510-3110=-1610)
6) 100000-1
(1000002+1111102=111102+12=111112
3210-1110=3110 )
Задание 6. Умножьте двоичные числа (С=АВ). Проверьте результат путем перевода аргументов и произведения в десятичную систему счисления (А2А10, В2В10, С2С10)
1) 101010 = 10100(2010)
(1010210 = 2010)
2) 11111111= 11011001 (21710)
(7103110 = 21710)
3) 1010100 = 101000 (4010)
(1010410 = 4010)
4) 110110 = 100100 (3610)
(610610= 3610)
5) 1101101 = 1000001 (6510)
(1310510 = 6510)
6) 1101100 = 110100 (5210)
(1310410
= 5210)
Задание 7. Выполните деление двоичных чисел (D=A:В). Проверьте результат путем перевода аргументов и частного в десятичную систему счисления (А2А10, В2В10,D2D10)
1) 1011101:1010 = 1001.010011 (9.310)
(9310:1010 = 9.310)
2) 10101010:101 = 100010 (3410)
(17010:510 = 3410)
3) 1101010:110 = 10001.1010101 (17.6610)
(10610:610 = 17.6610)
4) 1011010:1000 = 1011.01 (11.2510)
(9010:810 = 11.2510)
Задание 8. Выполните действия над восьмеричными числами
1) 101+727 = 10308 2) 15100 = 15008
3) 106-54 = 328 4) 1477 = 13648
5) 0.77+0.34= 1.338 6) 2460:12 = 204.63148
Задание 9. Выполните действия над шестнадцатеричными числами
1) 781 + 78A = F0B16 2) A05 : BE = D.816
3) FED + 123 = 111016 4) FA.B : C8 = 1.40E147AE16
5) FF - 8C = 7316 6) D5A 100 = D5A0016
Задание 10. Определите количество целых чисел, кратных :
а) 1112 в интервале (-11102 ; 1111012),
Ответ: 10 чисел кратных 7 в интервале (-14;61)
б) 1112 в интервале (-B16 ; 2518);
Ответ: 24 чисел кратных 7 в интервале (-11; 169)
Задание 11. Определите двузначное десятичное число, для которого справедливо равенство XY5 = YX7 .
Решение:
Сделаем развернутую запись чисел:
51*X+50*Y=71*Y+70*X
5*X+Y=7*Y+X
4*X=6*Y
X=1.5*Y
X и Y могут быть равны числам от 1 до 4 т.к в пятеричной системе счисления есть только эти цифры.
При Y = 2 получаем X= 3
325 = 1710 = 237
Ответ: Двузначное целое десятичное число для которого справедливо равенство XY5 = YX7 это 1710.
Задание 12. Трехзначное число, записанное в системе счисления с основанием 3, при перестановке крайних цифр становится числом, выражающим то же количество, но уже в системе счисления с основанием 4. Определите это число.
Решение:
Это число 211
211(3)=2*32+1*3+1=22(10)
112(4)=1*42+1*4+2=22(10)
Задание 13. Определите наименьшее основание позиционной системы счисления х, при котором 145x = 442y .
Решение:
145x=1*x2+4*x+5;
442y=4*y2+4*y+2;
X2+4x+5=4y2+4y+2;
X2+4x+5 = (x+2)2+1;
4y2+4y+2 = (2y+1)2+1;
(x+2)2+1 = (2y+1)2+1;
X+2=2y+1;
X = 2y-1;
Так как в 145x и в 442y
есть цифры 5 и 4, то можно сделать вывод что X>5 и Y>4.
Путем подстановки X = 2*5-1 = 9;
1459 = 4425 = 12210
Ответ: Наименьшее основание позиционной системы счисления х, при котором 145x = 442y равняется 9.
Задание 14. Трехзначное число, записанное в шестнадцатеричной системе счисления, увеличивается вдвое от перестановки первой цифры в конец числа. Определите максимальное из таких чисел, записанное в системе счисления по основанию 16.
Решение:
Пусть наше число равно abc.
Максимальное число можно получить, если сложение в двух младших разрядах будет идти через перенос.
2c = a + 16
2b +1 = c + 16
2a + 1 = b
Сокращаем и получаем:
2с = a + 16
c = 2b - 15
b = 2a + 1
Подставляем значения:
2с = a + 16
c = 4a – 13
7a = 42
a = 6
Из уравнения b = 2a + 1 получаем b = 2*6+1 = 13
1310 = D16
Из уравнения 2с = a + 16
получаем c = 11 = 13
1110 = B16
Объединив все значения в abc получим число 6DB16
Контрольная работа № 3 по информатике
Тема: «Алгебра логики»
Задание 1: Составьте таблицу истинности логического выражения:
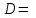
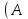 и не
и не 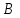
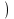 и не
и не 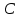 и не
и не 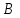 или
или 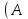 и
и 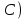 .
.| A | B | C | 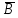 | A ∧ 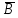 | 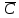 | А ∧ 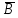 ∧ ∧ 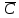 | A ∧ 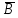 ∧ 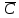 ∧ ∧ 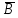 | A ∧ C | A ∧ 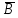 ∧ ∧ 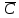 ∧ ∧ 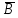 ∨ A ∧ C ∨ A ∧ C |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |

