ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.03.2024
Просмотров: 1084
Скачиваний: 0
СОДЕРЖАНИЕ
1. ОБЩАЯ ХАРАКТЕРИСТИКА НЕФТЯНОЙ ЗАЛЕЖИ
1.1. Понятие о нефтяной залежи
1.2. Механизм использования пластовой энергии при добыче нефти
2. ИСТОЧНИКИ ПЛАСТОВОЙ ЭНЕРГИИ
2.2. Приток жидкости к скважине
2.3. Режимы разработки нефтяных месторождений
3. ТЕХНОЛОГИЯ И ТЕХНИКА ВОЗДЕЙСТВИЯ НА ЗАЛЕЖЬ НЕФТИ
3.1. Цели и методы воздействия
3.2. Технология поддержания пластового давления закачкой воды
3.3. Основные характеристики поддержания пластового давления закачкой воды
3.5. Техника поддержания давления закачкой воды
3.6. Оборудование кустовых насосных станций
3.7. Технология и техника использования глубинных вод для ППД
3.8. Поддержание пластового давления закачкой газа
3.9. Методы теплового воздействия на пласт
3.10. Техника закачки теплоносителя в пласт
4. ПОДГОТОВКА СКВАЖИН К ЭКСПЛУАТАЦИИ
4.1. Конструкция оборудования забоев скважин
4.2. Приток жидкости к перфорированной скважине
4.3. Техника перфорации скважин
4.5. Методы освоения нефтяных скважин
4.6. Передвижные компрессорные установки
4.7. Освоение нагнетательных скважин
5. МЕТОДЫ ВОЗДЕЙСТВИЯ НА ПРИЗАБОЙНУЮ ЗОНУ СКВАЖИНЫ
5.1. Назначение методов и их общая характеристика
5.2. Обработка скважин соляной кислотой
5.4. Поинтервальная или ступенчатая СКО
5.5. Кислотные обработки терригенных коллекторов
5.6. Техника и технология кислотных обработок скважин
5.7. Гидравлический разрыв пласта
5.8. Осуществление гидравлического разрыва
5.9. Техника для гидроразрыва пласта
5.10. Тепловая обработка призабойной зоны скважины
5.11. Термогазохимическое воздействие на призабойную зону скважины
5.12. Другие методы воздействия на призабойную зону скважин
6.1. Назначение и методы исследования скважин
6.2. Исследование скважин при установившихся режимах
6.3. Исследование скважин при неустановившихся режимах
6.4. Термодинамические исследования скважин
6.5. Скважинные дебитометрические исследования
6.6. Техника и приборы для гидродинамических исследований скважин
7. ОСНОВЫ ТЕОРИИ ПОДЪЕМА ЖИДКОСТИ В СКВАЖИНЕ
7.1. Физика процесса движения газожидкостной смеси в вертикальной трубе
7.2. Уравнение баланса давлений
7.3. Плотность газожидкостной смеси
8. ЭКСПЛУАТАЦИЯ ФОНТАННЫХ СКВАЖИН
8.1. Артезианское фонтанирование
8. 2. Фонтанирование за счет энергии газа
8. 4. Расчет фонтанного подъемника
8. 5. Расчет процесса фонтанирования с помощью кривых распределения давления
8. 6. Оборудование фонтанных скважин
8. 7. Регулирование работы фонтанных скважин
8. 8. Осложнения в работе фонтанных скважин и их предупреждение
9. ГАЗЛИФТНАЯ ЭКСПЛУАТАЦИЯ СКВАЖИН
9.1. Общие принципы газлифтной эксплуатации
9.2. Конструкции газлифтных подъемников
9.3. Пуск газлифтной скважины в эксплуатацию (пусковое давление)
9.4. Методы снижения пусковых давлений
9.6. Принципы размещения клапанов
9.7. Принципы расчета режима работы газлифта
9.9. Системы газоснабжения и газораспределения
9.11. Исследование газлифтных скважин
10. ЭКСПЛУАТАЦИЯ СКВАЖИН ШТАНГОВЫМИ НАСОСАМИ
10.1. Общая схема штанговой насосной установки, ее элементы и назначение
10.2. Подача штангового скважинного насоса и коэффициент подачи
10.3. Факторы, снижающие подачу ШСН
10.4. Оборудование штанговых насосных скважин
10.5. Исследование скважин, оборудованных штанговыми насосными установками
10.6. Эксплуатация скважин штанговыми насосами в осложненных условиях
11. эксплуатация скважин погружными центробежными электронасосами
11.1. Общая схема установки погружного центробежного электронасоса
11.2. Погружной насосный агрегат
11.3. Элементы электрооборудования установки
11.4. Установка ПЦЭН специального назначения
11.5. Определение глубины подвески ПЦЭН
11.6. Определение глубины подвески ПЦЭН c помощью кривых распределения давления
12.1. Принцип действия гидропоршневого насоса
12.2. Подача ГПН и рабочее давление
14. РАЗДЕЛЬНАЯ ЭКСПЛУАТАЦИЯ ПЛАСТОВ ОДНОЙ СКВАЖИНОЙ
14.2. Некоторые схемы оборудования скважин для раздельной эксплуатации пластов
14.3. Раздельная закачка воды в два пласта через одну скважину
15.3. Технология текущего ремонта скважин
15.4. Капитальный ремонт скважин
15.5. Новая технология ремонтных работ на скважинах
16. ЭКСПЛУАТАЦИЯ ГАЗОВЫХ СКВАЖИН
16.1. Особенности конструкций газовых скважин
16.2. Оборудование устья газовой скважины
16.3. Подземное оборудование ствола газовых скважин при добыче природного газа различного состава
16.4. Оборудование забоя газовых скважин
16.5. Расчет внутреннего диаметра и глубины спуска колонны НКТ в скважину
16.6. Способы и оборудование для удаления жидкости с забоя газовых и газоконденсатных скважин
16.7. Одновременная раздельная эксплуатация двух газовых пластов одной скважиной
где r - газовый фактор, приведенный к термодинамическим условиям рассматриваемого сечения.
При Сг = Сж b = 1 и из (7.25) следует
Этот случай соответствует идеальным условиям, при которых образуется идеальная смесь плотностью ρи. Относительная скорость газа (по отношению к жидкости)
или
Подставляя (7.28) в (7.23), получим
 , (7.29)
, (7.29)Поскольку а > 0, то b > 1. Увеличение скорости газа при неизменном объемном расходе V уменьшает fг, следовательно, увеличивает fж. В результате плотность смеси, как это следует из (7.18) и (7.19), увеличивается. Таким образом, явление скольжения газа (a > 0) при неизменных объемных расходах q и V приводит к утяжелению смеси по сравнению с идеальным случаем. Поэтому чем больше а, тем больше потребуется давление на забое для поднятия данного количества жидкости.
Плотность реальной смеси
где Δρ - увеличение плотности смеси, обусловленное скольжением. Для определения Δρ к (7.25) прибавим и отнимем ρи согласно (7.26), получим

Группируя слагаемые и делая некоторые преобразования, имеем

или после приведения к общему знаменателю в квадратных скобках и группировки слагаемых найдем
 . (7.31)
. (7.31)Из сопоставления (7.31), (7.30) и (7.26) следует
 . (7.32)
. (7.32)При b = 1 (отсутствие скольжения газа Сг = Сж) числитель в (7.32) обращается в нуль и Δρ = 0. Утяжеление ГЖС не происходит. С увеличением b (b > 1) Δρ монотонно увеличивается (рис. 7.9). Заштрихованная часть графика показывает увеличение плотности ГЖС за счет скольжения газа.
Из формулы (7.29) видно, что при одной и той же относительной скорости газа (a = const) b уменьшается при увеличении Сж, т. е. расхода жидкости. Отсюда следует важный для практики вывод - переход на трубы малого диаметра при определенных условиях за счет увеличения Сж уменьшит величину b, а это в свою очередь повлечет уменьшение Δρ.
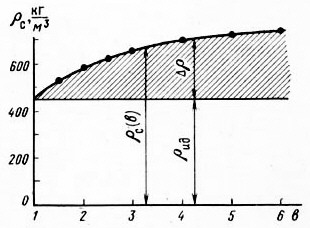
Pиc. 7.9. Изменение плотности ГЖС в результате скольжения газа
Поэтому подъем ГЖС может быть осуществлен при меньшем давлении в нижней части трубы (при меньшем забойном давлении). Однако целесообразность перехода на трубы меньшего диаметра должна быть проверена расчетом, так как при этом возрастут потери давления на трение.
В теории движения ГЖС существуют важные понятия, через которые определяется плотность смеси. Это расходное газосодержание β и истинное газосодержание φ. Расходное газосодержание потока ГЖС определяется как отношение объемного расхода газа V к общему расходу смеси V+q:
 . (7.33)
. (7.33)Истинное газосодержание потока ГЖС учитывает скольжение газа и поэтому является отношением площади, занятой газом fг, ко всему сечению трубы f:
Тогда
Из сопоставления (7.35) и (7.25) следует
Разделив в (7.33) числитель и знаменатель на q и используя обозначение (7.24), получим
Отнимая в (7.38) по единице и меняя знак, получим
или
Сопоставляя (7.39), (7.38) и (7.26), видим, что
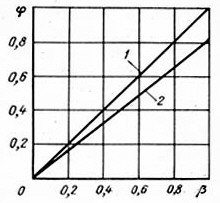
Рис. 7. 10. Зависимость φ от β при отсутствии скольжения газа
(β = φ, линия 1) и при скольжении ( φ < β, линия 2)
Таким образом, плотность идеальной смеси (7.40) определяется расходным газосодержанием β, а плотность реальной смеси (7.35) - истинным φ.
Найдем формулы связи между φ, β, b и r. Из (7.37) и (7.38) имеем
откуда
Решая (7.38) относительно г, найдем
 . (7.42)
. (7.42)Подставляя (7.42) в (7.41), получим
 .
.Откуда после преобразований
 . (7.43)
. (7.43)Решая (7.43) относительно b, получим
 . (7.44)
. (7.44)При движении ГЖС возможны два предельных случая, когда по трубе движется одна жидкость fг = 0, следовательно, φ также равно нулю, и когда по трубе движется один газ fж = 0. Аналогично и для расходного газосодержания β. Поэтому физически возможными пределами изменениями φ и β будут 0 < φ <1, 0< β < 1. При отсутствии скольжения газа относительная его скорость равна нулю (а = 0), следовательно, Сг = Сж, b = 1 и из формулы (7.43) φ = β.
Таким образом, φ(β) для идеального подъемника будет являться прямой в виде диагонали квадрата линия 1 (рис.7.10).
Во всех других случаях при b > 1 , т. е. при а > 0 (Сг > Сж), получим φ = β .
На диаграмме φ(β) линия 2 проходит ниже диагонали. Чем больше скольжение, т. е. чем больше а, а следовательно, и b, тем ниже пройдет линия φ(β).
Относительная скорость газа а зависит от следующих факторов: дисперсности газовых пузырьков, а следовательно, структуры движения ГЖС; вязкости жидкой фазы; разности плотностей газа и жидкости, от которой зависит подъемная сила; диаметра трубы и газонасыщенности потока ГЖС.
Попытки теоретического определения величины а не дают надежных результатов. Поэтому оценка относительной скорости газа проводится главным образом экспериментально и составляет основной предмет исследований. По некоторым рекомендациям предлагается принять φ = 0,833·β во всем диапазоне значений β представляющем практический интерес. Величина β всегда известна, так как расходами V и q либо задаются, либо вычисляют для заданных термодинамических условий.
7.4. Формулы перехода
В литературе по вопросам движения ГЖС для вычисления рс различные авторы используют различные выражения и различные подходы к определению этой важной величины. Покажем, что все возможное разнообразие подходов к определению ρс может быть осуществлено с помощью формул перехода, связывающих основные величины, определяющие ρс, такие как β, φ, r, b, а, C, Cж, Сг.
Ранее были получены следующие выражения:
где
 . (7.49)
. (7.49)Из сопоставления (7.45) и (7.47) следует
Так как при отсутствии скольжения Сг = Сж, b = 1. Из сопоставления (7.45) и (7.48) получим
Используя (7.50) и (7.51) и подставляя их в (7.49), получим
Решая (7.50) относительно r, найдем
 . (7.53)
. (7.53)Решая (7.51) относительно r, найдем
 . (7.54)
. (7.54)Приравнивая (7.53) и (7.54) и решая относительно b, найдем
 . (7.55)
. (7.55)Решая (7.55) относительно φ, найдем
 . (7.56)
. (7.56)При необходимости вычислить φ через относительную скорость газа а такое вычисление может быть сделано следующим образом. Имеем
 . (7.57)
. (7.57)Формулу (7.57) можно выразить через β

