ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.03.2024
Просмотров: 956
Скачиваний: 0
СОДЕРЖАНИЕ
1. ОБЩАЯ ХАРАКТЕРИСТИКА НЕФТЯНОЙ ЗАЛЕЖИ
1.1. Понятие о нефтяной залежи
1.2. Механизм использования пластовой энергии при добыче нефти
2. ИСТОЧНИКИ ПЛАСТОВОЙ ЭНЕРГИИ
2.2. Приток жидкости к скважине
2.3. Режимы разработки нефтяных месторождений
3. ТЕХНОЛОГИЯ И ТЕХНИКА ВОЗДЕЙСТВИЯ НА ЗАЛЕЖЬ НЕФТИ
3.1. Цели и методы воздействия
3.2. Технология поддержания пластового давления закачкой воды
3.3. Основные характеристики поддержания пластового давления закачкой воды
3.5. Техника поддержания давления закачкой воды
3.6. Оборудование кустовых насосных станций
3.7. Технология и техника использования глубинных вод для ППД
3.8. Поддержание пластового давления закачкой газа
3.9. Методы теплового воздействия на пласт
3.10. Техника закачки теплоносителя в пласт
4. ПОДГОТОВКА СКВАЖИН К ЭКСПЛУАТАЦИИ
4.1. Конструкция оборудования забоев скважин
4.2. Приток жидкости к перфорированной скважине
4.3. Техника перфорации скважин
4.5. Методы освоения нефтяных скважин
4.6. Передвижные компрессорные установки
4.7. Освоение нагнетательных скважин
5. МЕТОДЫ ВОЗДЕЙСТВИЯ НА ПРИЗАБОЙНУЮ ЗОНУ СКВАЖИНЫ
5.1. Назначение методов и их общая характеристика
5.2. Обработка скважин соляной кислотой
5.4. Поинтервальная или ступенчатая СКО
5.5. Кислотные обработки терригенных коллекторов
5.6. Техника и технология кислотных обработок скважин
5.7. Гидравлический разрыв пласта
5.8. Осуществление гидравлического разрыва
5.9. Техника для гидроразрыва пласта
5.10. Тепловая обработка призабойной зоны скважины
5.11. Термогазохимическое воздействие на призабойную зону скважины
5.12. Другие методы воздействия на призабойную зону скважин
6.1. Назначение и методы исследования скважин
6.2. Исследование скважин при установившихся режимах
6.3. Исследование скважин при неустановившихся режимах
6.4. Термодинамические исследования скважин
6.5. Скважинные дебитометрические исследования
6.6. Техника и приборы для гидродинамических исследований скважин
7. ОСНОВЫ ТЕОРИИ ПОДЪЕМА ЖИДКОСТИ В СКВАЖИНЕ
7.1. Физика процесса движения газожидкостной смеси в вертикальной трубе
7.2. Уравнение баланса давлений
7.3. Плотность газожидкостной смеси
8. ЭКСПЛУАТАЦИЯ ФОНТАННЫХ СКВАЖИН
8.1. Артезианское фонтанирование
8. 2. Фонтанирование за счет энергии газа
8. 4. Расчет фонтанного подъемника
8. 5. Расчет процесса фонтанирования с помощью кривых распределения давления
8. 6. Оборудование фонтанных скважин
8. 7. Регулирование работы фонтанных скважин
8. 8. Осложнения в работе фонтанных скважин и их предупреждение
9. ГАЗЛИФТНАЯ ЭКСПЛУАТАЦИЯ СКВАЖИН
9.1. Общие принципы газлифтной эксплуатации
9.2. Конструкции газлифтных подъемников
9.3. Пуск газлифтной скважины в эксплуатацию (пусковое давление)
9.4. Методы снижения пусковых давлений
9.6. Принципы размещения клапанов
9.7. Принципы расчета режима работы газлифта
9.9. Системы газоснабжения и газораспределения
9.11. Исследование газлифтных скважин
10. ЭКСПЛУАТАЦИЯ СКВАЖИН ШТАНГОВЫМИ НАСОСАМИ
10.1. Общая схема штанговой насосной установки, ее элементы и назначение
10.2. Подача штангового скважинного насоса и коэффициент подачи
10.3. Факторы, снижающие подачу ШСН
10.4. Оборудование штанговых насосных скважин
10.5. Исследование скважин, оборудованных штанговыми насосными установками
10.6. Эксплуатация скважин штанговыми насосами в осложненных условиях
11. эксплуатация скважин погружными центробежными электронасосами
11.1. Общая схема установки погружного центробежного электронасоса
11.2. Погружной насосный агрегат
11.3. Элементы электрооборудования установки
11.4. Установка ПЦЭН специального назначения
11.5. Определение глубины подвески ПЦЭН
11.6. Определение глубины подвески ПЦЭН c помощью кривых распределения давления
12.1. Принцип действия гидропоршневого насоса
12.2. Подача ГПН и рабочее давление
14. РАЗДЕЛЬНАЯ ЭКСПЛУАТАЦИЯ ПЛАСТОВ ОДНОЙ СКВАЖИНОЙ
14.2. Некоторые схемы оборудования скважин для раздельной эксплуатации пластов
14.3. Раздельная закачка воды в два пласта через одну скважину
15.3. Технология текущего ремонта скважин
15.4. Капитальный ремонт скважин
15.5. Новая технология ремонтных работ на скважинах
16. ЭКСПЛУАТАЦИЯ ГАЗОВЫХ СКВАЖИН
16.1. Особенности конструкций газовых скважин
16.2. Оборудование устья газовой скважины
16.3. Подземное оборудование ствола газовых скважин при добыче природного газа различного состава
16.4. Оборудование забоя газовых скважин
16.5. Расчет внутреннего диаметра и глубины спуска колонны НКТ в скважину
16.6. Способы и оборудование для удаления жидкости с забоя газовых и газоконденсатных скважин
16.7. Одновременная раздельная эксплуатация двух газовых пластов одной скважиной
откуда
 . (7.1)
. (7.1)Плотность смеси в трубке rс зависит от расхода газа V. Чем больше V, тем меньше rс. Изменяя V, можно регулировать Н. При некотором расходе V = V1 величина Н может достигнуть L. При V
Можно представить другой крайний случай, когда к башмаку подъемной трубы подводится так много газа, что при постоянном перепаде давления DР = Р1 - Р будет идти только газ, DР будет расходоваться на преодоление всех сопротивлений, вызванных движением по трубе чистого газа. Расход этого газа пусть будет V=V3. Если к башмаку подать еще больший расход (V>V3), то излишек газа не сможет пройти через подъемную трубу, так как ее пропускная способность при данных условиях (L, d, DP) равна только V3, и устремится мимо трубы, оттесняя от башмака жидкость. Очевидно, при этом расход жидкости будет равен нулю (q = 0). Таким образом, из этого опыта можно сделать следующий вывод.
1. При V
2. При V = V1 q = 0 (H = L) (начало подачи).
3. V1 < V < V2 0 < q < qmax (H > L),
4. При V = V2 q = qmax (точка максимальной подачи).
5. При V2 < V < V 3 qmax > q > 0.
6. При V = V3 q = 0 (точка срыва подачи).
Обычно правая ветвь кривой q(V) (рис. 7.2) пологая, левая крутая.
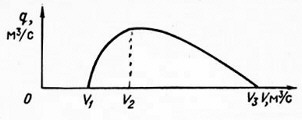
Рис. 7.2. Зависимость подачи q газожидкостного подъемника от расхода газа V
Для всех точек кривой постоянным является давление P1, так как погружение h в процессе опыта не изменялось. Существует понятие - относительное погружение e = h / L. Таким образом, для данной кривой ее параметром будет величина относительного погружения ε.
7.1.2. Зависимость положения кривых q (V) от погружения
Поскольку при наших рассуждениях никаких ограничений на величину e не накладывалось, то при любых e, лежащих в пределах 0 < e < 1, вид соответствующих кривых q(V) будет одинаковый. При увеличении е новые кривые q(V) обогнут прежнюю, так как с ростом h потребуется меньший расход газа для наступления перелива. По тем же причинам возрастет qmax, а точка срыва подачи на соответствующих кривых сместится вправо. При уменьшении e все произойдет наоборот. Новые кривые q(V) расположатся внутри прежних и при e = 0 кривая q(V) выродится в точку. Другой предельный случай - e = 1 ( h = L, 100% погружения). В этом случае при бесконечно малом расходе газа немедленно произойдет перелив. Точка начала подачи сместится в начало координат. Кривая q(V) для e = 1 начнется в начале координат и обогнет все семейство кривых. Таким образом, каждый газожидкостный подъемник характеризуется семейством кривых q(V), каждая из которых будет иметь свой параметр e (рис. 7.3).
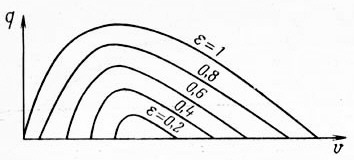
Рис. 7.3. Семейство кривых q(V) для газожидкостного подъемника данного диаметра
7.1.3. Зависимость положения кривых q(V) от диаметра трубы
В наших рассуждениях никаких ограничений на диаметр подъемной трубы и на ее длину не накладывается. Поэтому аналогичное семейство кривых q(V) должно существовать для подъемников любого диаметра и любой длины. Однако возникает вопрос, как располагать повое семейство кривых для трубы диаметром d2 > d1 по отношению к прежним кривым. Увеличение диаметра потребует большого расхода газа, так как
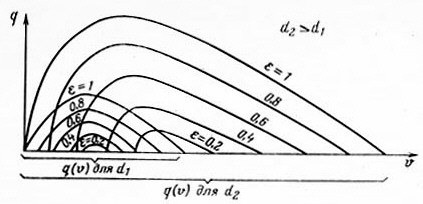
Рис. 7.4. Семейство кривых q(V) для двух газожидкостных подъемников различных диаметров
объем жидкости, который необходимо разгазировать для достижения данной величины rс, при прочих равных условиях ( h = const, L = const) возрастает пропорционально d2. Пропускная способность трубы по жидкости, газу или газожидкостной смеси (ГЖС) также возрастет. Поэтому для увеличенного диаметра будет существовать также семейство кривых q(V), все точки которого будут смещены вправо, в сторону увеличенных объемов, кроме одной точки, совпадающей с началом координат для кривой q(V) при e = 1. В каждом из этих семейств и любых других, кривые q(V) при значениях e, близких к единице и к нулю, не имеют практического значения, так как они либо неосуществимы (e = 0), либо бессмысленны (e = 1), и введены в рассуждения только для понимания физики процессов, происходящих при движении ГЖС в трубах.
7.1.4. К. п. д. процесса движения ГЖС
На каждой кривой q(V) имеется еще одна характерная и очень важная точка, точка так называемой оптимальной производительности, соответствующая наибольшему к. п. д. Если проанализировать произвольную кривую q(V), для которой e = const, то для нее будут справедливы следующие рассуждения.
Из определения понятия к. п. д. следует, что
 . (7.2)
. (7.2)Полезная работа заключается в поднятии жидкости с расходом q на высоту L - h, так что
Затраченная работа - это работа газа, расход которого, приведенный к стандартным условиям, равен V. Полагая для простоты, что процесс расширения газа изотермический, на основании законов термодинамики идеальных газов можем записать
 , (7.4)
, (7.4)где Р1 + Рo - абсолютное давление у башмака; Р2 + Ро - то же на устье, Ро - атмосферное давление.
Подставляя (7.3) и (7.4) в (7.2), получим
 . (7.5)
. (7.5)В (7.5) все величины, кроме q и V, постоянны, так как рассматривается одна кривая q(V), для которой ε = const. Следовательно, для данной кривой
где С - константа.
Поэтому к. п. д. будет иметь максимальное значение в той точке, в которой отношение q / V максимально. Но q / V = tg φ, так как q - ордината, V - абсцисса, φ - угол наклона прямой, проведенной из начала координат через данную точку (q, V). Только для касательной tgφ будет иметь максимальное значение, так как только для нее угол φ максимален. Поэтому в точке касания прямой, проведенной из начала координат с кривой q(V), получаются такой дебит q и такой расход газа V, при которых к. п. д. процесса будет наибольшим. Расход q при максимальном к. п. д. называют оптимальным дебитом qoпт.
Таким образом, для любой кривой q(V), имеющей ε = const, оптимальный расход жидкости определится как точка касания касательной, проведенной из начала координат.
7.1.5. Понятие об удельном расходе газа
Удельным расходом газа называют отношение
 . (7.7)
. (7.7)Из определения следует, что для точек начала и срыва подачи, когда q = 0, а V > 0, удельный расход R обращается в бесконечность. Для режима оптимальной подачи, когда к. п. д. максимален, R минимально. Это очевидно, так как при максимальном

Рис. 7.5. Зависимость удельного расхода газа R от общего расхода газа V для данной кривой q (V)
к. п. д. должно расходоваться минимально возможное количество газа на подъем единицы объема жидкости. При режиме максимальной подачи (qmax) η < ηmax. Поэтому и удельный расход газа R будет при этом режиме больше оптимального. Величина R может быть получена для любой точки кривой q(V) путем деления абсциссы на ординату данной точки (рис. 7.5).
7.1.6. Зависимость оптимальной и максимальной подач от относительного погружения
Для любого семейства кривых q(V), построенного для данного диаметра труб, можно найти qmax и qопт и проследить их зависимость от изменения относительного погружения ε. С увеличением ε величины qmax также увеличиваются по криволинейному закону (см. рис. 7.3 и 7.4). Что касается qопт, то последние, во-первых, всегда остаются меньше соответствующих qmax и, во-вторых, сначала увеличиваются с ростом ε, а затем при 0,5 < ε < 1 начинают уменьшаться. В частности, при ε = 1 кривая q(V) выходит из начала координат. Поэтому касательная, проведенная из начала координат, будет иметь точку соприкосновения с кривой q(V) в начале координат. Это
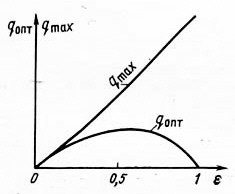
Рис. 7.6. Зависимость оптимальной qопт и максимальной qmax подачи от относительного нагруження ε
означает для q(V) при ε = 1 qопт = 0. Таким образом, величины qопт должны сначала увеличиваться, затем уменьшаться и при ε = 1 обращаться в нуль. Наибольшая величина qопт достигается при ε = 0,5 - 0,6 (рис. 7.6). Это подтверждается и многочисленными опытами различных исследователей. Отсюда можно сделать важный для практики вывод: для достижения наибольшей эффективности работы газожидкостного подъемника необходимо осуществить погружение подъемной трубы под уровень жидкости на 50 - 60% (ε = 0,5 - 0,6) от всей длины трубы L. Однако эта рекомендация в реальных условиях не всегда может быть выполнена из-за низкого динамического уровня или из-за ограниченного давления газа, используемого для этой цели.
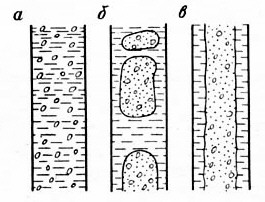
Рис. 7.7. Структуры газожидкостного потока: а - эмульсионная; б - четочная; в – стержневая
7.1.7. Структура потока ГЖС в вертикальной трубе
В зависимости от физических свойств жидкости и характера ввода газа в поток могут возникать различные структуры движения ГЖС в трубе, которые существенным образом влияют на энергетические показатели подъема жидкости. В фонтанных скважинах на участке НКТ, где давление меньше давления насыщения, выделяющийся из нефти свободный газ образует тонкодисперсную структуру, называемую эмульсионной. Мелкие газовые пузырьки более или менее равномерно пронизывают массу нефти, образуя практически однородную квазигомогенную смесь газа и жидкости. Вследствие своей малости (доли мм) и большой плотности газовые пузырьки обладают малой архимедовой силой. Поэтому их скорость всплытия относительно жидкости пренебрежимо мала и в расчетах может не учитываться. Это происходит до тех пор, пока в результате уменьшения давления при движении смеси вверх по трубе газовые пузырьки, расширяясь, увеличивают объемное газосодержание потока до 20 - 25%. При дальнейшем уменьшении давления и поступлении из нефти новых количеств газа пузырьки, сливаясь, образуют глобулы больших размеров, измеряемые в диаметре несколькими сантиметрами. Скорость всплытия таких глобул в результате действия архимедовой силы становится большой, достигая нескольких десятков сантиметров в секунду. Это ухудшает энергетические показатели процесса подъема. Такая структура называется четочной.
При больших расходах газа возникает стержневая структура, при которой газ с распыленными в нем каплями жидкости движется непрерывным потоком, увлекая за собой по стенкам трубы волнистую пленку жидкости. При стержневой структуре движения скорость газа по отношению к жидкости достигает нескольких метров в секунду. Между эмульсионной, четочной и стержневой структурами не существует резких границ перехода и тем не менее некоторые исследователи выделяют и переходные структуры от эмульсионной к четочной, и от четочной к стержневой (рис. 7.7). На возникновение той или иной структуры существенное влияние оказывает вязкость нефти, а также наличие в ней различных ПАВ, способствующих диспергации газа в потоке.
7.2. Уравнение баланса давлений
При проектировании или анализе работы установок для подъема жидкости из скважин, когда по НКТ движется ГЖС, основным вопросом является определение потерь давления, связанных с этим движением. Рассматривая некоторый участок вертикальной трубы, в которой движется ГЖС, можно записать
где Р1 - давление в нижней части трубы, Рс - давление, уравновешивающее гидростатическое давление столба ГЖС, Ртр - потери давления на преодоление сил трения при движении ГЖС, Рус - потери давления на создание ускорения потока ГЖС, так как его скорость при движении в сторону меньших давлений увеличивается из-за расширения газа; Р2 - противодавление на верхнем конце трубы.
Уравнение (7.8) справедливо для всех случаев: короткой и длинной трубы, вертикальной и наклонной и является основным при расчете потерь давления и их составляющих.
При практических расчетах могут возникнуть две основные задачи, когда известно давление вверху Р2 и требуется определить давление внизу Р1 или наоборот. При этом все другие условия, такие как длина трубы, ее диаметр, расход поднимаемой жидкости, свойства жидкости и газа и другие, должны быть известны. Это так называемые прямые задачи. Но могут возникать и другие задачи, которые можно назвать обратными, когда, например, требуется определить расход поднимаемой жидкости q при заданном перепаде давления Р1 - Р2. Или определить необходимое количество газа Го для подъема заданного количества жидкости q при заданном перепаде давления Р1 - Р2 и ряд других задач. Во всех случаях необходимо знать слагаемые, входящие в уравнение баланса давления (7.8).
Обозначим ρ - плотность жидкости, L - длина трубы по вертикали, ρс - плотность ГЖС, h - потеря напора на трение на участке трубы длиной в 1 м столба ГЖС, hус - потеря напора на ускорение на участке трубы длиной в 1 м столба ГЖС.
Тогда
Деля все слагаемые на ρgL, найдем
 . (7.10)
. (7.10)Слева от знака равенства написана величина, которая является действующим перепадом (Р1 - Р2), выраженным в метрах столба поднимаемой жидкости, отнесенным к 1 м длины трубы. Эту величину обозначают
 . (7.11)
. (7.11)При Р2 = 0 (истечение в атмосферу) величина ε совпадает с тем относительным погружением (ε = h / L), о котором шла речь при рассмотрении физической характеристики процесса движения ГЖС.
Выражение (7.11) является более общим, так как учитывает противодавление P2. Уравнение (7.9) может быть записано в дифференциальной форме при L → 0
или в конечных разностях
Величины ρc, hтр, hyc зависят от термодинамических условий потока, изменяющихся с глубиной, и в первую очередь существенно зависят от давления. Эти условия непрерывно изменяются вдоль трубы и их аналитический учет достаточно сложен. Задача сводится к интегрированию уравнения (7.12) в пределах от 0 до L, либо к численному суммированию приращений давления, определяемых (7.13), также в пределах от 0 до L. Чем меньше участки трубы ΔL, на которые может быть разбита вся длина подъемных труб, тем меньше будут изменяться слагаемые, входящие в уравнение баланса давления.
Если для таких коротких участков трубы рассчитать падение давления ΔPi, то общий перепад составит сумму
 . (7.14)
. (7.14)где
Из (7.14) следует, что если известно давление вверху Р2 , то
 . (7.16)
. (7.16)Если известно давление внизу P1, то

. (7.17)
Таким образом, задача сводится к расчету потерь давления на коротких участках подъемника при заданных параметрах движения (q, d, Г, ρ и пр.) и последующем их суммировании. Очевидно, чем больше n, т. е. чем меньше ΔL, тем точнее будет такое решение. Однако практика подобных вычислений показывает, что при n = 10 - 15 достигается достаточная точность.
7.3. Плотность газожидкостной смеси
Через данное сечение трубы при движении по ней ГЖС проходит некоторое количество газа и жидкости. Можно представить, что все газовые пузырьки занимают в сечении трубы суммарную площадь fг, а жидкость - остающуюся площадь в том же сечении fж, так что
где f - площадь сечения трубы (рис. 7.8). Плотность ГЖС в таком случае определится как средневзвешенная
где ρж и ρг - плотность жидкости и газа при термодинамических условиях сечения.
Обычно fг / f обозначают через φ. Тогда fж / f = 1 - φ,
Величина φ = fг / f называется истинным газосодержанием потока.
Обозначим V - объемный расход газа через данное сечение; q - объемный расход жидкости через то же сечение; Сг - линейная скорость движения газа относительно стенки трубы; Сж - линейная скорость движения жидкости относительно стенки трубы.
Тогда можно записать следующие соотношения:
 . (7.20)
. (7.20)и
 . (7.21)
. (7.21)Подставляя (7.20) и (7.21) в (7.18) и делая некоторые сокращения, получим
 , (7.22)
, (7.22)В восходящем потоке газ движется быстрее жидкости, так как на него действует архимедова сила выталкивания. Обозначим
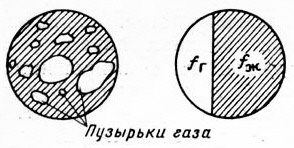
Рис. 7.8. Среднестатистические площади в трубе, занятые газом и жидкостью
 , (7.23)
, (7.23)Разделив числитель и знаменатель в (7.22) на q и вводя новые обозначения согласно (7.23) и (7.24), получим
