МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ

ФГБОУ ВО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Теоретическая механика»

КУРСОВАЯ РАБОТА ПО РАЗДЕЛУ "ДИНАМИКА"

«ИССЛЕДОВАНИЕ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ»

Рецензия на курсовую работу

Курсовая работа по содержанию

соответствует

/

не соответствует

выданному заданию и выполнена

в полном объеме

/

не в полном объеме.

Курсовая работа может быть допущена к защите с добавлением ____ баллов

рецензента после успешной защиты.

Рецензент

(ФИО)

(Подпись)

(Дата)

Вариант № 10-1

Выполнил: студент гр.

№ студенческого билета:

Научный руководитель:

Тула 2020 г

Оглавление


Аннотация

Дана механическая система с одной степенью свободы – совокупность абсолютно твердых тел, связанных друг с другом с помощью невесомых нерастяжимых нитей, параллельных данным плоскостям. Система снабжена внешней упругой связью с коэффициентом жесткости с. На первое тело системы действует сила сопротивления 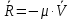и возмущающая гармоническая сила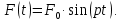

---

Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения. Проскальзывание нитей на блоках отсутствует. Применяя основные теоремы динамики системы и аналитические методы теоретической механики, определен закон движения первого тела и реакции внешних и внутренних связей; произведен численный анализ полученного решения с использование компьютерных технологий.

Схема механизма и данные для выполнения курсовой работы

СХЕМА МЕХАНИЗМА


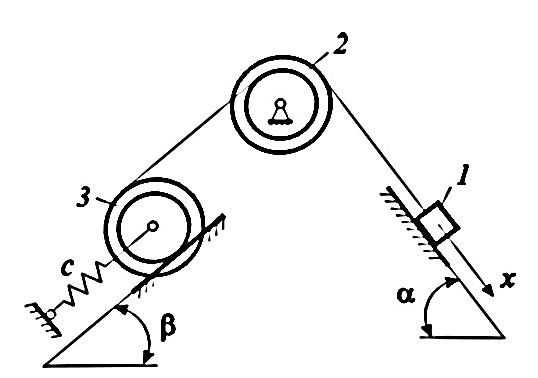
ДАННЫЕ ДЛЯ РАСЧЕТА

m₁=4mα=60° m= 1 кг

m₂=mβ=30° r= 0.1 м

m₃=2m ₀=4 см/с с=4000 Н/м

r₂=rS₀=3 см μ=100 Н*сек/м

r₃=r φ=0.1 F₀=50 Н

R₂=2rp=3.14 рад/с

R₃=3r

i₂=3/2r
i₃=2r

Часть 1. Применение основных теорем динамики.

1.1. Постановка второй основной задачи динамики системы.

Обозначения (рис.2):
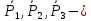силы тяжести, 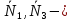нормальные реакции опорных плоскостей,

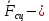сила сцепления, 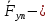упругая реакция пружины,

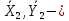реакция подшипника блока 2, 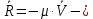сила вязкого сопротивления,

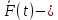возмущающая сила.

Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 3 происходит без скольжения). Будем определять ее положение с помощью координаты

---

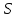
. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1.

Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:



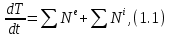
где Т - кинетическая энергия системы,

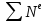- сумма мощностей внешних сил,

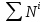- сумма мощностей внутренних сил.

Теорема (1.1) формулируется так: "Производная по времени от кинетической энергии механической системы равна алгебраической сумме мощностей внешних и внутренних сил, действующих на точки механической системы".

Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1-3:



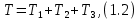
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:



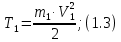
Блок 2 совершает вращательное движение около неподвижной оси. Его кинетическая энергия:



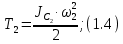
где 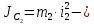момент инерции относительно центральной оси блока,

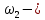угловая скорость блока.

Каток 3 совершает плоскопараллельное движение, поэтому его кинетическая энергия определяется по теореме Кёнига:



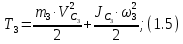
где 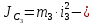момент инерции относительно центральной оси катка,

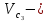скорость центра масс катка,

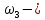угловая скорость блока.

Кинетическая энергия всего механизма будет равна:




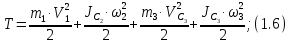
Выразим 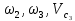через скорость груза 1:

---

;



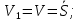
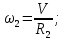
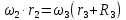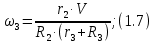
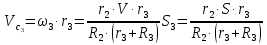
Подставляя кинематические соотношения (1.7) в выражение (1.6) получаем:



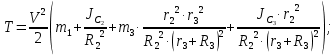
или

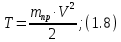
где 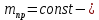приведенная масса: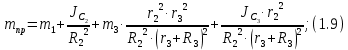







;

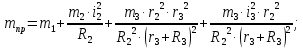
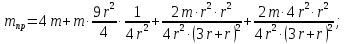
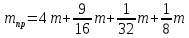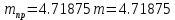кг.

Найдем производную от кинетической энергии по времени:



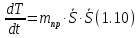
Вычислим сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения:



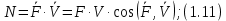
Рассматриваемая нами механическая система является неизменяемой, т. е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:



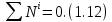
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы:

.

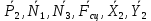Сумма мощностей остальных сил:



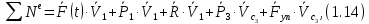
или, раскрывая скалярные произведения



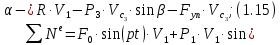
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил определим:

(

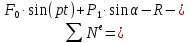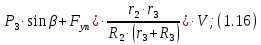
или ,

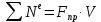где

---

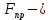
приведенная сила.

Упругую силу считаем пропорциональной удлинению пружины, которое равно сумме статического ( 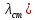и динамического удлинений: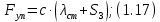


где 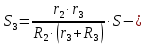динамическое удлинение.

Сила вязкого сопротивления 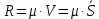,тогда:

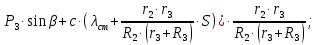( (1.18)

В состоянии покоя приведенная сила равна нулю. Полагая 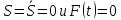, получаем условие равновесия:

(

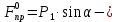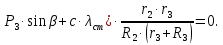
Отсюда статическое удлинение пружины ( 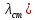равно: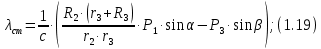


Подставляя выражение (1.20) в (1.19), получаем окончательное выражение приведенной силы:

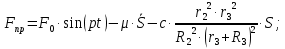(1.20.)

Подставим выражения для производной от кинетической энергии (1.10) и сумму мощностей всех сил с учетом (1.20) в уравнение (1.1), получаем дифференциальное уравнение движения системы:



_;

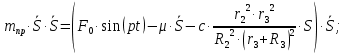
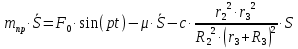или 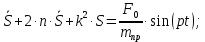(1.21)
где 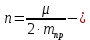показатель степени затухания колебаний

,




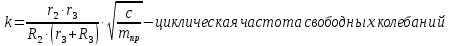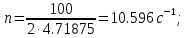
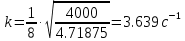
Начальные условия движения:

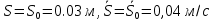(1.22)

Выражения (1.21) и (1.22) совместно представляют математическую модель для решения второй задачи динамики.

1.2. Определение закона движения системы.

Проинтегрируем дифференциальное уравнение (1.21). Пусть возмущающая сила изменяется по гармоническому закону:

---

Смотрите также файлы

• Программирование линейных алгоритмов.doc

• Решение текстовых задач Учитель Хамзина Меруерт Толегеновна.pptx

• Инженерное оборудование и маскировка позиций.doc

• Решение задач на проценты. Сложные проценты.docx

• Особенности составления сводной бухгалтерской отчетности.doc