Файл: Курсовая работа по разделу "динамика" исследование колебаний механической системы с одной степенью свободы.docx
Добавлен: 17.03.2024
Просмотров: 46
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
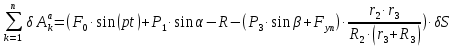
Аналогичное выражение для приведенной силы
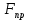получили ранее (см. 1.20).Найдем возможную работу сил инерции:
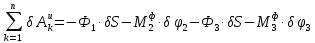
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
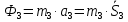
Используя кинематические соотношения (1.3), можно записать
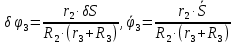
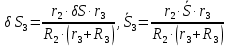
Тогда возможную работу сил инерции можно преобразовать к виду:
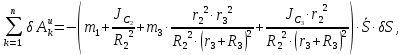
где
;
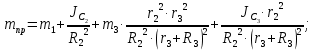
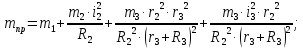
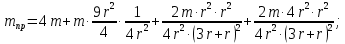
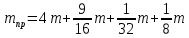кг.Подставляем выражения (3.2) и (3.3) в общее уравнение динамики (3.1), получаем:
Поделив это уравнение на
получим дифференциальное уравнение колебаний системы:или
где
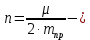показатель степени затухания колебаний,
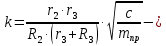циклическая частота свободных колебаний
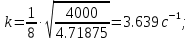
Начальные условия движения:
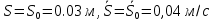
3.2. Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода.
Составим теперь уравнение Лагранжа 2-го рода. В качестве обобщенной координаты примем перемещение груза 1 –
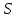. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид: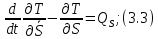
где
– кинетическая энергия системы;
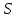– обобщенная сила; – обобщенная координата;
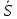– обобщенная скорость.Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1-3, образующих механическую систему:
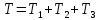
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
Блок 2 совершает вращательное движение около неподвижной оси. Его кинетическая энергия:
где
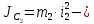момент инерции относительно центральной оси блока,
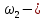угловая скорость блока.Каток 3 совершает плоскопараллельное движение, поэтому его кинетическая энергия определяется по теореме Кёнига:
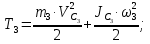
где
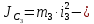момент инерции относительно центральной оси катка,
скорость центра масс катка,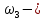
угловая скорость блока.
Кинетическая энергия всего механизма будет равна:
Выразим
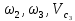через скорость груза 1: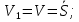
; 
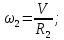
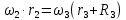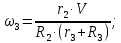
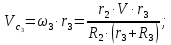
Подставляя кинематические соотношения в выражение
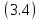получаем: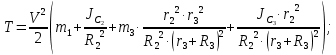 
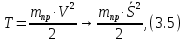
где
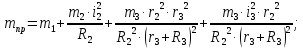
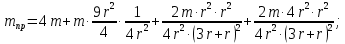
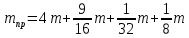; кг Аналогичное выражение было получено ранее (1.9).
Производные от кинетической энергии:
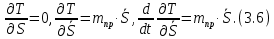
Для определения обобщенной силы
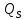сообщим системе возможное перемещение 
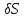и вычислим сумму элементарных работ всех активных сил (3.2):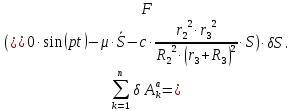
С другой стороны, для системы с одной степенью свободы:
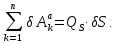
Сравнивая два последних соотношения, получаем:
Подставляя производные (3.6) и обобщенную силу (3.7) в уравнение Лагранжа (3.3)
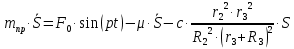
или
где
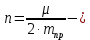
показатель степени затухания колебаний,
циклическая частота свободных колебаний,
Начальные условия движения:
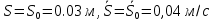.Приложение
----------------------------------------------------------------
Фамилия: Куприн, Имя: Алексей, Отчество: Сергеевич
Группа: 621781. , Вариант: 10
-----------------------------------------------------------------
M1= 6.000 M2= 1.000 M3= 2.000 M4= 0.000
i1= 0.000 i2= 0.150 i3= 0.200 i4= 0.000
r1= 0.000 r2= 0.100 r3= 0.100 r4= 0.000
R1= 0.000 R2= 0.200 R3= 0.300 R4= 0.000
Mu=100.000 C=4000.000 F0= 50.000 P= 3.140
S0= 0.030 V0= 0.040 alfa= 1.047 beta= 0.000
-----------------------------------------------------------------
K= 3.050 n= 7.442 K1= 6.788 Мпр= 6.719 Cпр= 62.500
+-------+-------+-------+-------+-------+-------+-------+-------+
| T | S | V | W | T12 | T23 | T34 | Fsc |
+-------+-------+-------+-------+-------+-------+-------+-------+
| 0.000| 0.005| 0.011| -0.163| 50.750|101.683| 0.000|305.212|
| 0.050| -0.009| -0.476| 7.069| 63.926|119.900| 0.000|352.631|
| 0.100| -0.036| -0.571| 8.429| 72.851|136.219| 0.000|400.227|
| 0.150| -0.063| -0.452| 6.612| 79.097|150.756| 0.000|445.655|
| 0.200| -0.080| -0.243| 3.478| 83.738|163.563| 0.000|487.211|
| 0.250| -0.087| -0.022| 0.171| 87.403|174.614| 0.000|523.670|
| 0.300| -0.083| 0.172| -2.707| 90.384|183.813| 0.000|554.146|
| 0.350| -0.070| 0.322| -4.913| 92.752|191.031| 0.000|578.006|
| 0.400| -0.051| 0.425| -6.418| 94.454|196.129| 0.000|594.804|
| 0.450| -0.028| 0.487| -7.297| 95.388|198.987| 0.000|604.257|
| 0.500| -0.003| 0.515| -7.666| 95.450|199.523| 0.000|606.235|
| 0.550| 0.023| 0.516| -7.636| 94.559|197.708| 0.000|600.761|
| 0.600| 0.048| 0.496| -7.304| 92.676|193.569| 0.000|588.012|
| 0.650| 0.072| 0.462| -6.744| 89.803|187.193| 0.000|568.324|
| 0.700| 0.094| 0.415| -6.008| 85.984|178.728| 0.000|542.191|
| 0.750| 0.113| 0.358| -5.135| 81.299|168.374| 0.000|510.257|
| 0.800| 0.130| 0.294| -4.155| 75.855|156.383| 0.000|473.305|
| 0.850| 0.143| 0.224| -3.091| 69.786|143.049| 0.000|432.238|
| 0.900| 0.152| 0.150| -1.967| 63.243|128.698| 0.000|388.063|
| 0.950| 0.158| 0.073| -0.807| 56.388|113.685| 0.000|341.862|
| 1.000| 0.159| -0.006| 0.365| 49.395| 98.379| 0.000|294.770|
| 1.050| 0.157| -0.084| 1.525| 42.436| 83.156| 0.000|247.944|
| 1.100| 0.151| -0.160| 2.644| 35.684| 68.393| 0.000|202.534|
| 1.150| 0.141| -0.232| 3.699| 29.306| 54.452| 0.000|159.657|
| 1.200| 0.128| -0.298| 4.662| 23.461| 41.676| 0.000|120.367|
| 1.250| 0.111| -0.357| 5.511| 18.291| 30.381| 0.000| 85.632|
| 1.300| 0.092| -0.407| 6.225| 13.924| 20.844| 0.000| 56.306|
| 1.350| 0.071| -0.448| 6.787| 10.467| 13.299| 0.000| 33.110|
| 1.400| 0.048| -0.477| 7.182| 8.006| 7.933| 0.000| 16.615|
| 1.450| 0.023| -0.495| 7.401| 6.601| 4.876| 0.000| 7.227|
| 1.500| -0.002| -0.500| 7.438| 6.286| 4.205| 0.000| 5.177|
| 1.550| -0.026| -0.493| 7.292| 7.070| 5.936| 0.000| 10.515|
| 1.600| -0.051| -0.474| 6.967| 8.931| 10.026| 0.000| 23.110|
| 1.650| -0.074| -0.443| 6.470| 11.826| 16.374| 0.000| 42.652|
| 1.700| -0.095| -0.402| 5.814| 15.683| 24.825| 0.000| 68.661|
| 1.750| -0.114| -0.350| 5.015| 20.406| 35.171| 0.000|100.496|
| 1.800| -0.130| -0.290| 4.093| 25.880| 47.156| 0.000|137.376|
| 1.850| -0.143| -0.223| 3.070| 31.970| 60.487| 0.000|178.391|
| 1.900| -0.152| -0.150| 1.971| 38.526| 74.835| 0.000|222.534|
| 1.950| -0.157| -0.074| 0.824| 45.387| 89.848| 0.000|268.719|
| 2.000| -0.159| 0.004| -0.343| 52.385|105.155| 0.000|315.809|
| | | | | | | | |
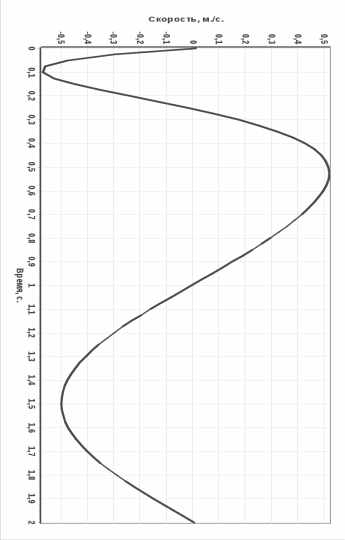
Анализ результатов
В данной курсовой работе проведено исследование динамического поведения механической системы с использованием основных теорем и уравнений теоретической механики. Дифференциальное уравнение системы было получено тремя способами. Во всех трех случаях коэффициенты
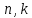, масса 
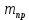и сила
получились одинаковыми.Следовательно, они получены правильно.
Используя основные теоремы динамики системы и аналитические методы теоретической механики, мы определили закон движения первого тела, его скорость и ускорение; реакции внешних и внутренних связей. Однако, из-за того, что исходные данные для расчета были выбраны произвольно, в некоторый момент наблюдалось провисание нитей, что привело бы к неверному описанию реального движения механизма полученным законом движения.
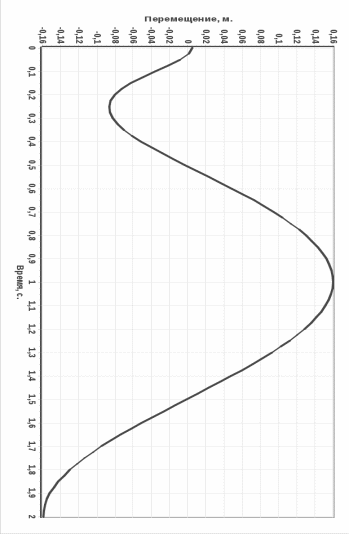
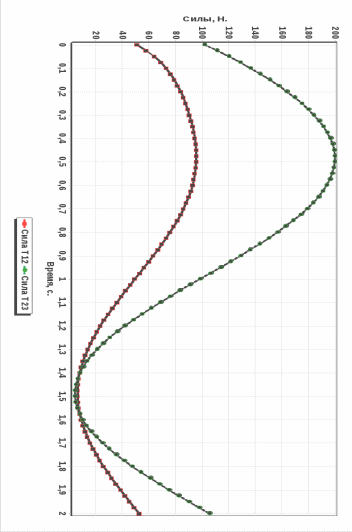
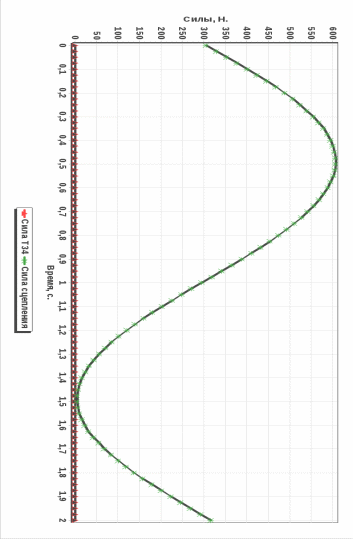
Для приведения в соответствие реального закона движения с полученным на основе теорем, мы провели оптимизацию данных, в результате чего рекомендуется изменить массу первого тела с 4 до 6 кг. Графики изменения характеристик механической системы представлены в разделе «Приложение».
Список литературы:
1. Методические указания для выполнения курсовой работы по разделу «Динамика» «Исследование колебаний механической системы с одной степенью свободы».
2. Конспекты лекций по разделу «Динамика».
3. Никитин Н.Н. Курс теоретической механики. - М.: Высшая школа, 1990.– 607 с.
4. Яблонский А.А. Курс теоретической механики. Т.2. - М.: Высшая школа,1984. - 424 с.