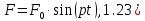
где амплитуда возмущающей силы,

циклическая частота возмущения.
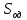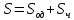Общее решение S неоднородного дифференциального уравнения складывается из общего решения однородного уравнения и частного решения неоднородного: . Однородное дифференциальное уравнение, соответствующее данному неоднородному, имеет вид:



Составим характеристическое уравнение и найдем его корни.



Отсюда получаем:

;



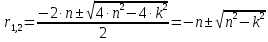
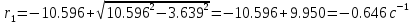Так как решение однородного уравнения имеет вид: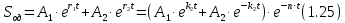

;

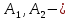постоянные интегрирования

где .

Определяем частное решение неоднородного дифференциального уравнения:



Частное решение дифференциального уравнения ищем в виде правой части:

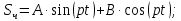(1.27)

Подставляя (2.4) в (2.2), после несложных преобразований получаем:

;

Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных А и В:

;



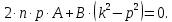
Решая эту систему, получаем следующие выражения для коэффициентов А и В:

---

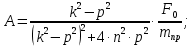
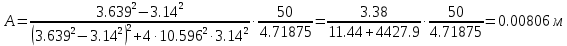м





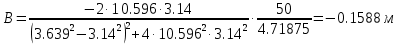
Таким образом, решение (1.27) определено. Складывая (1.25) и (1.27), получаем общее решение дифференциального однородного уравнения в виде:





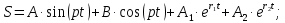
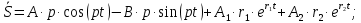
Постоянные интегрирования определяются из начальных условий.
при 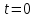получается: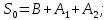




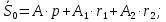
Решая эту систему получаем:









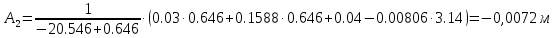
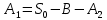
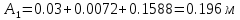
Закон движения имеет вид:







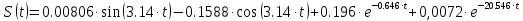
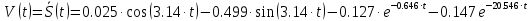
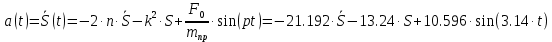
1.3. Определение реакций внешних и внутренних связей.

Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (Приложение, рис.3).

Определение реакций связей проведем с помощью теоремы об изменении количества движения 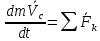(изменение количества движения системы за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени)

и теоремы об изменении кинетического момента относительно центра масс

(производная по времени от момента количества движения (кинетического момента) механической системы относительно какой-либо неподвижной оси равна главному моменту всех внешних сил).

Для тел запишем сначала теоремы в векторной форме, потом в проекционной.

---

Тело 1:
Теорема об изменении количества движения для тела 1 векторной форме:



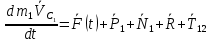
В проекции на ось :

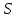В проекции на ось :

Теорема об изменении кинетического момента относительно центра масс для тела 1:

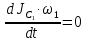, так как тело не совершает вращательных движений.

Тело 2:

Теорема об изменении количества движения для тела 2 в векторной форме:



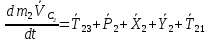
В проекции на ось :


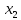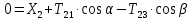
В проекции на ось :

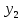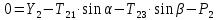
Теорема об изменении кинетического момента относительно центра масс для тела 2:





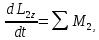
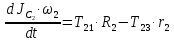
Тело 3:

Теорема об изменении количества движения для тела 2 в векторной форме:



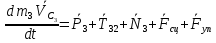
В проекции на ось :

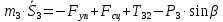
В проекции на ось :

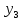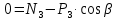
Теорема об изменении кинетического момента относительно центра масс для тела 3:





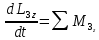
С учетом кинематических соотношений (1.3) систему уравнений преобразуем к виду:

---

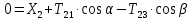
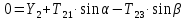
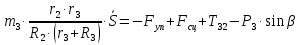
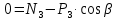
Уравнения составляют систему алгебраических уравнений относительно функций:



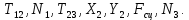
Решая эту систему, получаем выражения для определения реакций:

















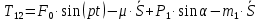
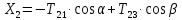
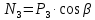
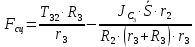
Часть 2.Построение алгоритма вычислений.

2.1.Исходные данные:



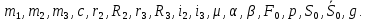
2.2.Вычисление констант:























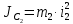
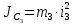
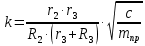
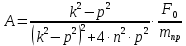
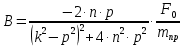
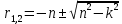
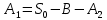
2.3. Задание начального значения времени:

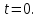
2.4. Вычисление значения функции в момент времени :

---

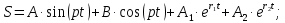
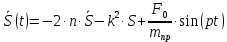
2.5. Вычисление реакций связей: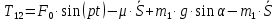















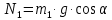
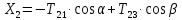
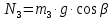
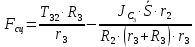
2.6. Вывод на печать значений искомых функций в момент времени .

2.7.Определение значений времени на следующем шаге .

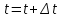2.8. Проверка условия окончания цикла

2.9. Возврат к пункту 2.4.

Часть 3.Применение принципа Даламбера-Лагранжа и уравнений Лагранжа 2-го рода.
3.1. Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.

Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа:








.
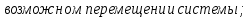
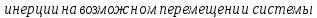Изобразим на рисунке активные силы и силы инерции (рис. 4). Реакции идеальных связей

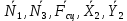не учитываем и не отображаем на расчетной схеме, поскольку по определению работа из реакций на любом возможном перемещении системы равна нулю. Пружина является неидеальной связью. Введем реакцию этой связи в число активных сил.

Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:



Вычисляя последовательно элементарные работы активных сил и суммируя их получаем:

---

Смотрите также файлы

• Программирование линейных алгоритмов.doc

• Решение текстовых задач Учитель Хамзина Меруерт Толегеновна.pptx

• Инженерное оборудование и маскировка позиций.doc

• Решение задач на проценты. Сложные проценты.docx

• Особенности составления сводной бухгалтерской отчетности.doc