8. Моделирование и оптимизация фондового портфеля

8.1. Доходность и риск фондового портфеля
Портфель – это организованная совокупность N ценных бумаг (или, без нарушения общности, пакетов ценных бумаг), каждая из которых характеризуется своей первоначальной ценой вхождения в портфель S_i0.

Итого первоначальная стоимость портфеля, сформированного в момент времени Т=0:

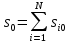
Можно сказать, что в начальный момент времени формирования портфеля, складывается долевое распределение весов активов в портфеле



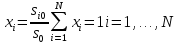
Сформированный портфель немедленно начинает изменять свои ценовые характеристики во времени. Часть активов портфеля растёт, часть – падает. Соответственно, в момент T каждый компонент имеет цену S_iT, а весь портфель – цену S_T.

Курсовая доходность i-го актива портфеля (процентов годовых), измеренная в момент времени Т, может быть оценена по формуле:

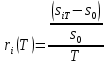
Аналогично для портфеля в целом, его курсовая доходность, как случайная величина, линейно зависит от доходности отдельных активов в составе портфеля (также случайных величин).
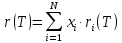
Т.е., мы при анализе портфеля здесь и далее уходим от использования его ценовых характеристик, оперируя с доходностями компонент портфеля.
Если мы говорим о доходностях как о случайных величинах, вероятностное распределение которых можно получить, то уместно моделировать портфель в вероятностной парадигме.

Наиболее ходовым вариантом вероятностного моделирования является представление портфеля N-мерной случайной величиной доходности:

r = (r1, r2, ..., rN)

причём характеристики случайной величины доходности являются константами, не зависящими от времени наблюдения (т.е. не являются функциями времени), причём каждая из компонент портфеля имеет нормальное вероятностное распределение.
Нормальное распределение случайной величины доходности характеризуется двумя параметрами – математическим ожиданием ri (будем обозначать его той же буквой, что и саму случайную величину) и среднеквадратическим отклонением σi

---

Между отдельными случайными величинами доходности в составе единой N-мерной величины R существует стохастическая связь, которая характеризуется корреляционной матрицей {ρij}, коэффициенты которой характеризуют связь между доходностями i-ой и j-ой бумаг.

Если ρij = -1, то это означает полную отрицательную корреляцию, если ρij = +1 – имеет место полно положительная корреляция. Всегда выполняется ρii = 1, так как ценная бумага полно положительно коррелирует сама с собой.
Поскольку все компоненты портфеля распределены нормально, то и результирующая доходность по портфелю распределена нормально (это следует из свойств нормального распределения). Тогда математическое ожидание распределения курсовой доходности по портфелю:

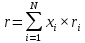
среднеквадратическое отклонение (СКО) доходности портфеля от среднего (σ):
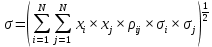
Пример 1

Портфель составлен из двух акций, параметры которых приведены в таблице

№	х	r, % год	σ, % год
1	0,3	10	3
2	0,7	20	5

Акции некоррелированы (ρij = 0 при i ≠ j). Определить доходность и волатильность портфеля.

Решение.

Имеем 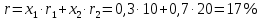годовых

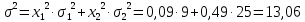(% год)²

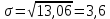% годовых

Чтобы оценить риск портфеля, необходимо установить норматив L на предельно низкий размер доходности по портфелю, % годовых. Если доходность оказывается ниже нормативного значения, фиксируется негатив. Вероятность наступления негативного события критического снижения доходности – это и есть риск, оцениваемый формулой



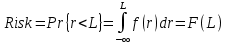
Где F(*) – функция распределения случайной величины доходности актива (или портфеля), f(*) – плотность распределения.

Пример 2.

Портфель бескупонных облигаций обладает среднеожидаемой доходностью r=10% годовых и СКО σ= 3% годовых. Установлен норматив предельной доходности L = 6% годовых. Определить риск портфеля.

---

Решение.

Функция распределения F(6% год.)=0.09.
Мы получили значение риска, но мы не можем интерпретировать его в качественных терминах, оценить насколько велико или мало полученное значение. Чтобы перейти от количественной оценке риска к качественной, необходимо перейти от вероятностной функции распределения вида F(*) к стандартному виду функции нормального распределения Ф(*) с мат.ожиданием 0 и дисперсией 1.

Тогда выполняется условие учёта сдвига и масштаба в стандартном нормальном распределении:

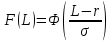
Исследуя вид функции Ф(*) и темпы её роста с ростом L, можно предложить следующие правила нормирования фактора риска:

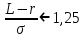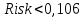- - если , то является приемлемым значением и во всех случаях может быть принят (неснижаемый уровень)

- - если 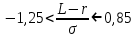, то 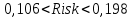этот уровень является пограничным. Такой риск может быть принят только с оговорками, с применением специальных мер по снижению уровня риска. К таким мерам, в частности, может быть отнесено внедрение в портфель хеджирующих (страхующих) фондовых опционов.

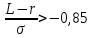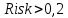- - если , то является неприемлемым для рационального инвестора
Пример 2 (продолжение)

Полученный риск является полностью приемлемым.

При этом .




8.2. Портфель из двух бумаг
Формулы ТВ:

Дисперсия:

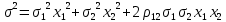
Риск:

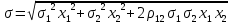
где ρ12 – коэффициент корреляции двух бумаг; σ – риск бумаги; х – ценовая доля бумаги.

Доходность портфеля:

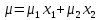
где μ – эффективность бумаги

Ковариация доходностей:

---

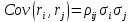
Отсюда

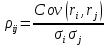
В случае независимых случайных величин 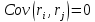, поэтому ковариация является мерой зависимости случайных величин.

Ковариационная матрица – матрица, элементами которой являются соответствующие ковариации ценных бумаг.

Для трех бумаг имеем



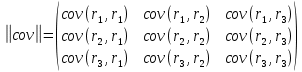
Тогда
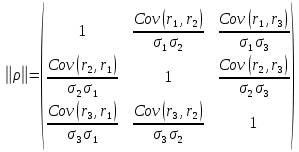
Пример 3. Дана ковариационная матрица 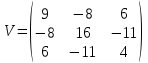. Найти корреляционную матрицу.

Решение.

Т.к. по диагонали в матрице V стоят дисперсии, то σ1=3, σ2=4, σ3=2


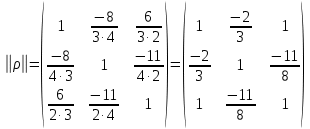
1. Случай полной корреляции

Здесь ρ=1.

Тогда 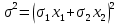и извлекая корень, получаем риски портфеля: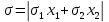

Т.к. все переменные неотрицательные, то, опуская модуль, получаем:



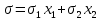
Если взять х1=1-t, x2=t, так что х1+х2=1, то



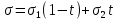
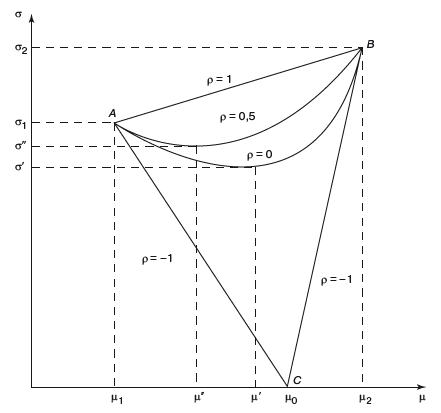
Это уравнение АВ. При t=0 портфель находится в т.А, при t=1, в т.В.

Если инвестор формирует портфель минимального риска, он должен включить в него бумагу 1 и портфель имеет вид Х=(1, 0). Доходность портфеля μ=μ1.

При формировании портфеля максимальной доходности, в него надо включить только бумагу, имеющую большую доходность, в данном случае бумагу 2 и портфель примет вид Х=(0, 1). Доходность μ=μ2.





2. Случай полной антикорреляции

Здесь ρ=-1.

Тогда

---

и извлекая корень, получаем риски портфеля:

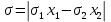
Допустимое множество портфелей представляет собой два отрезка АС и ВС.

Здесь возможен портфель нулевого риска (т.С(μ0, 0))

Имеем .

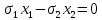Подставляя сюда х2=1-х1, получим

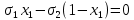
Т.е. 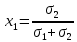и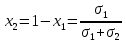

Т.о. портфель нулевого риска имеет вид

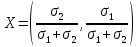
Его доходность равна
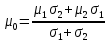
Пример 4. Для портфеля из двух бумаг с доходностью и риском соответственно (0,2; 0,5) и (0,4; 0,7) в случае полной антикорреляции найти портфель нулевого риска и его доходность.

Решение

Находим портфель нулевого риска



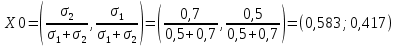
Тогда его доходность




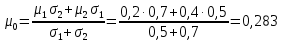
3. Независимые бумаги

Здесь ρ=0.

Тогда

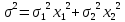
Найдем портфель минимального риска и его доходность и риск.

Т.е. надо минимизировать функцию 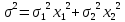при условии х1+х2=1

Это задача условного экстремума, решаемая методом Ланранжа:





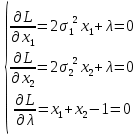
Из 1-го и 2-го имеем: 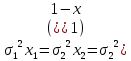, т.е.

Тогда портфель

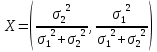
Его доходность

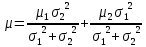
Риск
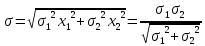
Пример 5. Пусть портфель состоит из двух независимых бумаг с рисками σ1=0,1 и σ2=0,2.

---

Смотрите также файлы

• Рязанский государственный медицинский университет имени академика И. П. Павлова.docx

• Цель Знакомство со звуками В, ВЬ, буквой В.docx

• Нарушения интонационной стороны речи у дошкольников с онр.docx

• Ингредиенты Способ приготовления.pdf

• Туберкулез (Tuberculosis).docx