Файл: 8. Моделирование и оптимизация фондового портфеля Доходность и риск фондового портфеля Портфель.docx
Добавлен: 18.03.2024
Просмотров: 135
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тогда риск портфеля равен
Т.о. иллюстрируется принцип диверсификации: при «размывании» портфеля по независимым бумагам его риск уменьшается
4. Безрисковая бумага
Пусть одна из бумаг портфеля – безрисковая.
Портфель из n бумаг, включая безрисковую называется портфелем Тобина.
Имеем две бумаги 1(μ1, 0) и 2(μ1, σ2), при этом μ1<μ2 (иначе необходимо было бы формировать портфель (1, 0), который уже был рассмотрен)
Тогда:
, 
, 
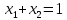
Отсюда допустимое множество портфелей
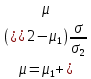является отрезкомПри σ=0 портфель находится в т.1(μ1, 0), при σ=σ2 – в т.2(μ2, σ2)
5. Портфель заданной эффективности
В случае портфеля из двух бумаг задание эффективности портфеля либо его риска однозначно определяет портфель.
При задании эффективности портфеля он однозначно находится из системы
Отсюда, при μ1≠μ2 имеем
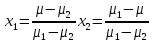
И квадрат риска равен
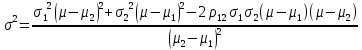
6. Портфель заданного риска
При задании риска портфель однозначно определяется из системы
После преобразований сводим систему к квадратному уравнению
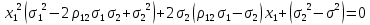
Отсюда
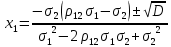
Где
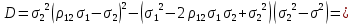
ПРИМЕРЫ ДЛЯ РЕШЕНИЯ
1. Портфель состоит из акций 4 видов, данные о которых представлены в таблице. Найти доходность портфеля.
2. Портфель состоит из акций 4 видов, данные о которых представлены в таблице. Найти доходность портфеля с помощью вычисления доходности каждой бумаги.
3. Доли ценных бумаг в портфеле, состоящем из 3 бумаг, равны х1=0,2, х2=0,3, х3=0,5. Матрица ковариаций равна
. Найдите риск портфеля.4. Портфель состоит из 3 активов А, В и С, взятых в равных ценовых долях. Ожидаемые доходности активов равны μ1=-15%, μ2=18%, μ3=23%. Найдите ожидаемую доходность портфеля.
5. Даны 5 видов акций, ожидаемая доходность и риск которых приведены в таблице. Выстроите акции в порядке предпочтения.
6. Портфель состоит из 3 бумаг А, В и С. Ценовая доля бумаги А равна 0,4, а ценовая доля бумаги В в 1,46 раза больше ценовой доли бумаги С. Найдите портфель.
7. Дана ковариационная матрица а)
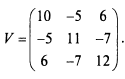б)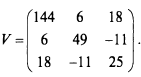
в)
. Найдите корреляционную матрицу.8. Данные о распределении доходностей 2 бумаг приведены в таблице. Найдите ковариацию и коэффициент корреляции этих бумаг
А)
Б)
В)
9. Доли ценных бумаг в портфеле равны х1=0,2, х2=0,3, х3=0,5, ожидаемые доходности μ1=-15%, μ2=18%, μ3=23%, ковариационная матрица имеет вид
. Найдите ожидаемую доходность и риск портфеля. 10. Портфель состоит из 2 бумаг А и В, ожидаемая доходность и риск которых, выраженные в процентах, равны А(14, 25) В(45, 60). Коэффициент корреляции равен 1. Найдите: а) портфель минимального риска; б) портфель максимальной доходности.
11. Портфель состоит из 2 бумаг А и В, ожидаемая доходность и риск которых, выраженные в процентах, равны А(15, 25) В(20, 88). Коэффициент корреляции равен 1. Риск портфеля составляет 75%. Найдите портфель и его доходность.
12. Портфель состоит из 2 бумаг А и В, ожидаемая доходность и риск которых, выраженные в процентах, равны А(12, 18) В(20, 47). Коэффициент корреляции равен -1. Найдите: а) доходность портфеля минимального риска; б) риск портфеля максимальной доходности. Изобразите график допустимого множества портфелей.
13. Портфель состоит из 2 бумаг А и В, ожидаемая доходность и риск которых, выраженные в процентах, равны А(20, 24) В(41, 36). Коэффициент корреляции равен -1. Доходность портфеля составляет 32%. Найдите портфель и его риск.
14. Портфель состоит из 2 бумаг А и В, ожидаемая доходность и риск которых, выраженные в процентах, равны А(50, 20) В(80, 60). Коэффициент корреляции равен 0. Найдите портфель минимального риска и его доходность.
15. Портфель минимального риска из 2 независимых бумаг (0,43; 0,23), (0,67; х) (первая цифра в скобках = доходность, вторая = риск) имеет вид (0,5; 0,5). Каковы риск второй бумаги, доходность и риск портфеля.
16. Портфель состоит из 2 бумаг А и В, ожидаемая доходность и риск которых, выраженные в процентах, равны А(20, 60) В(13, 45). Коэффициент корреляции равен -0,25. Найдите портфель минимального риска, его риск и доходность.