Файл: Астана аласы білім басармасы Математикалы сауаттылы факультатив курс бадарламасы астана, 2017.docx

Не оңай болды?

Не қиын болды?

Не білгіңіз келеді?

Мағынаны тану:

Логикалық есептерді оңай шығарудың алгоритмін слайд арқылы көрсету.

Рефлексия:

Оқушылар ауызша логикалық есептерді үш бөлімге бөліп қарастырады:

• 
  Жұмбақ есептер;
  
• 
  Сөзжұмбақ, ребус тапсырмалар;
  
• 
  Математикалық фокус есептер.
  

Қосымша тапсырмалар үлгілері
І. Белгілі бір заңдылық бойынша жазылған сандарды табу.

1-мысал. 200; 100; 300; 75... келесі санлы табыңыз.

Шешуі: Алғашқы екі санды қоссақ үшінші сан шығады, ал үшінші мен төртінші санды қоссақ біз іздеген сан шығады, сонда

300+75=375

Жауабы: 375

2-мысал. Шеңбер ішіндегі сандар беолігі бір заңдылықпен орналасқан. Сұрақ белгісінің орнына сәйкес келетін санды табыңыз.



Шешуі: Берілген шеңбердегі заңдылық мынадай:

2+3-1=4, 3+4-1=6, 6+9-1=14

22+14-1=35

Жауабы: 35

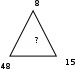
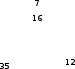
3 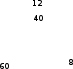-мысал: Сұрақ белгісінің орнына қандай сан сәйкес келетінің анықтаңыз:

Шешуі: Бірінші үшбұрыштың заңдылығын қарастырайық:

60-8=40+12

Екінші үшбұрыштың заңдылығы: 35-12=16+7

Ал, 48-15= 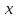+8 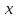=25 Жауабы: 25
Оқушылар ауызша логикалық есептерді үш бөлімге бөліп қарастырады:

• 
  Жұмбақ есептер;
  
• 
  Сөзжұмбақ, ребус тапсырмалар;
  
• 
  Математикалық фокус есептер.
  

Тақырыбы: Цифрлар және сандар туралы есептерді шешу 10.10.18

Мақсаты: Цифрлар және сандар туралы есептерді жылдам, әрі тез шығара алады

Формасы: жеке, жұптық

Әдіс-тәсілдер: АКТ, СТО, «Диалогтік оқыту» әдістері

Пән аралық байланыс: математика, логика

Қызығушылығын ояту.

1-мысал: 200-ден 401-ге дейінгі натурал сандар арасында толық квадрат бола алатын қанша сан бар екенін анықтаңыз

Шешуі:

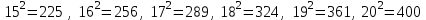
Жауабы: 6

2-мысал: Кітаптың беттерін нөмірлеу үшін 2322 цифр қолданылды. Нөмірлеу 1-ден басталса кітапта қанша бет болғанын анықтаңыз.

Шешуі: Берілген цифрлардың алғашқы 1-ден 9-ға дейінгі цифрлары 9 бет, ал 10-нан 99-ға дейінгі цифрлары 90 бет, 100-ден 2322-ге дейінгі цифрлары 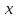бет құрады. Мынадай теңдеу құрамыз:

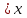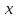9+180+3 =2322 =711

Сонда, 9+90+711=810 бет

Жауабы: 810 бет

3-мысал: 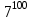саны қандай цифрмен аяқталады?

Шешуі: 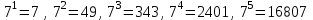екендігі белгілі. 7-ні дәрежелегенде сандардың соңғы цифрлары 7, 9, 3, 1, 7... заңдылығы бойынша құралады. Сонда 4 саннан кейін қайталанады: 100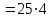

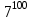=1 цифрымен аяқталады.

Жауабы: 1

4-мысал: Кітаптың 60 парағының қалыңдығы 1 см екендігі белгілі. Сол кітаптың 240 бетінің қалыңдығы қандай болады?

Шешуі: 60 парақта 120 бет бар

240 бетте 120 парақ. Сол себепті 240 беттің ұзындығы 2 см болады.

Жауабы: 2 см

5-мысал: 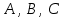- әртүрлі оң цифрлар. Сонымен қатар 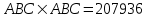. Бұл цифрлардың көбейтіндісін табыңыз.

?

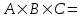Шешуі:



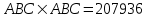
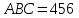
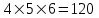
Жауабы: 120
Есептер шығару

№1 Екі жұмысшы бірігіп1000-нан аз деталь дайындауға тапсырма алды. Бірінші жұмысшы бірінші,екінші,үшінші күндері өз тапсырмасының 1/7,1/6 және 9/20 бөліктерін, ал екінші жұмысшы сол күндері сәйкесінше өз тапсырмасының ,3/11 және 3/7бөліктерін орындады. Әр жұмысшы үшінші күні қанша детальдан дайындады?
Шешуі. Әр күні дайындалатын детальдар саны бүтін болғандықтан,бірінші жұмысшының жасаған детальдар саны 7,6,20 сандарына,яғни 420 санына, екіншінің жұмысшының жасаған детальдарының саны 4,11,7 сандарына,яғни 308 санына қалдықсыз бөлінуі керек.Барлық детальдар саны 1000-нан кіші болғандықтан,бірінші жұмысшының жасаған детальдарының саны 420 (840 емес),ал екінші жұмысшының жасаған детальдарының саны 308 (616 немесе 924 емес). Демек, үшінші күні бірінші жұмысшы 189, ал екінші жұмысшы 132 деталь дайындаған.

№2.Дәл квадрат болатын төрт орынды санның бірінші цифры екіншісіне,ал үшіншісі төртіншісіне тең.Осы санды табыңыз.
Шешуі: Ізделінді сан 11-ге бөлінеді.Сондықтан,х=11(100а+в)болсын.11 жай сан және х дәл квадрат болғандықтан,100а+в саны 11-ге бөлінеді.100а+в=9*11*а+а+в тепе-теңдігінен а+в=11болу керектігін көреміз.Қосындысы 11 болатын цифрлар ішінен есеп шартын қанағаттандыратындары а=7, в= 4. Демек ізделінді сан 7744= 882
№3.
Бірдей цифрлармен жазылған 3 орынды сан 37-ге бөлінетіндігін дәлелде.
Дәлелдеу:
а*а*а =100а+10а+а= (74+26)а+10а+а =74а+37а =37(2а+1) , [10]
ІІІ Қортындылау

ІV Санның бөлінгіштік белгілері мен қасиеттерін еске түсіру.

Тақырыбы: Цифрлар және сандар туралы есептерді шешу 12.10.18

Мақсаты: Цифрлар және сандар туралы есептерді жылдам, әрі тез шығара алады(Бөлінгіштік белгілері)

Формасы: жеке, жұптық

Әдіс-тәсілдер: АКТ, СТО, «Диалогтік оқыту» әдістері

Пән аралық байланыс: математика

Сабақтың барысы

1.Бөлінгіштік белгілері

Бөлінгіштік белгілері деп, берілген х санының а санына қалдықсыз бөлінетінін бөлу амалын орындамай-ақ білуге болатын ережелерді атаймыз.

Сандар бөлінгіштігінің қасиеттері:

1) Егер а , в және а>0, онда а≥в.

2) Егер а cаны в-ге ,в саны а-ға бөлінсе, онда а=в.

3) Егер а саны в-ге, в саны с-ге бөлінсе, онда а саны с-ге бөлінеді.

4) Егер а; в сандары с-ге бөлінсе, кез келген натурал m және n үшін (ma+nв) cаны с-ге бөлінеді, егер ma> nв болса, онда (ma-nв) c-ге бөлінеді.

5) Егер а саны в-ге бөлінсе кез келген натурал к үшін ak саны в-ге бөлінеді.

6) Егер ak саны вk-ға бөлініп және k≠0 болса а саны в-ге бөлінеді.

7) n 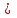N болса а 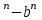саны а-в-ге, n тақ сан болса а 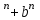саны а+в-ға бөлінеді. [2]

4-ке бөлінгіштік белгісі.

Егер санның соңғы екі цифрынан құралған сан 4-ке бөлінсе, онда берілген сан да 4-ке бөлінеді.

6-ға бөлінгіштік белгісі.

Егер берілген сан 2-ге және 3-ке бөлінсе, онда берілген сан да 6-ға бөлінеді.
7-ге бөлінгіштік белгісі.

7 сиқырлы сан деп есептелген. Өткен ғасырдың орта кезінен 7-ге бөлінгіштің мынандай белгісін білеміз. Ол былай есептеледі: берілген санның соңғы цифрын сызып тастап, сол сызылған санды екі еселеп берілген саннан азайтамыз. Осы әдісті ең соңында бір орынды сан қалғангға дейін жалғастырамыз. Егер осы бір орынды сан жетіге бөлінсе, онда берілген сан 7-ге бөлінеді. [13]

Берілген сан 7- ге бөлінетінін білу үшін: ол санды оңнан солға қарай үш – үштен топтаймыз да, тақ нөмірлі санды минуспен, ал жұп нөмірлі санды плюспен жазып, өрнектің мәнін табамыз. Егер өрнектің нәтижесі 7 – ге бөлінсе, онда берілген сан да 7 –ге бөлінеді.

8 –ге бөлінгіштік белгісі.

Егер берілген санның соңғы үш орынды саны 8 –ге бөлінсе, берілген сан да 8 –ге бөлінеді.

10- ға бөлінгіштік белгісі.

Жазылуы 0 цифрымен аяқталатын натурал сандар 10-ға бөлінеді.

11-ге бөлінгіштік белгісі.

Берілген сан 11-ге бөліну үшін ол санның жұп орындағы цифрларының қосындысы мен тақ орындағы цифрларының қосындысының айырмасы не нөл немесе 11-ге бөлінетін сан болу керек. [3]

Санның 11-ге бөлінетінін білу үшін: ол санды оңнан солға қарай екі –екіден топтаймыз да қосындысын табамыз. Сонда берілген сан 11- ге бөлінсе, берілген санда 11-ге бөлінеді.

13- ке бөлінгіштік белгісі.

Берілген санды солдан оңға қарай сызықшамен үш орынды сандарға бөлеміз. Бірінші, үшінші, бесінші орындағы бөліктердің қосындысын,содан соң екінші, төртінші,т.с.с. орындағылардың қосындысын тауып, сол қосындылардың айырмасы 13-ке бөлінсе, онда берілген сан да 13-ке бөлінеді. [3]
Берілген сан 13- ке бөлінетінін білу үшін: ол санды оңнан солға қарай үш – үштен топтаймыз да тақ нөмірлі санды минуспен, ал жұп нөмірлі санды плюспен жазып, өрнектің мәнін табамыз. Егер өрнектің нәтижесі 13-ке бөлінсе, онда берілген сан да 13-ке бөлінеді.

19- ға бөлінгіштік белгісі.

Сан 19- ға бөлінуі үшін ол санның ондықтары мен екі еселенген бірліктерінің қосындысы 19- ға бөлінуі керек.

25 – ке бөлінгіштік белгісі.

Сан 25- ке бөліну үшін, ол 00, 25, 50, 75, т.с.с. сандардың бірімен аяқталуы керек.
33-ке , 99-ға бөлінгіштік белгісі.

Сан 33-ке, 99-ға бөліну үшін, оның цифрларын оңнан солға қарай екі орыннан бөлгенде шыққан қосындысы 33-ке, 99-ға бөлінуі кеерк.
101-ге бөлінгіштік белгісі.

Егер берілген санның, оңнан солға қарай есептегенде екі–екіден бөлінген цифрларының тақ орындағылардың қосындысы мен жұп орындағылардың қосындысын бірінен –бірін ажыратқанда айырма не 0-ге, не 101 –ге тең болса ол сан 101 –ге бөлінеді.

1001 санының бөлінгіштігі

1001-саны Шехеризада саны. Бұл санның ерекшелігі неде? Мұның ерекшелігі мынада: бұл 1001 саны 7, 11, және 13 сандарына қалдықсыз бөлінеді немесе 1001=7*11*13 болады, бұл санның ерекшелігі бұл емес.

873*1001=873 873

555*1001=555 555 т.б.

Кез келген үш таңбалы санды 1001-ге көбейткенде шығатын көбейтіндіні үш таңбалы санды екі рет қайталап жазған санға тең. [6]

999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінгіштік белгілері.

999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінуі үшін оңнан солға қарай үш-үштен санағанда алғашқы үш бөліктің қосындысы, одан кейінгі үш бөліктің қосындысына тең болса және олар 999,333,111,37,27-ге бөлінетін болса,ол осы сандарға бөлінеді.

2. Есеп шығару №1 11-ге, 33-ке , 99-ға бөлінгіштік белгісі.2037354, 54+73+03+2= 132, 132:11= 12, 132:33 =4, ендеше 3037354 саны 11-ге де,33-ке де бөлінеді.

6918021, 6/91/80/21, 21+80+91+6 =198, 198:99= 2,198:33= 6,198:11= 18.

6918021 саны 11-ге, 33-ке,99-ға да бөлінеді.

№2 999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінгіштік белгілері.

776/223, 223+776 =999; 999= 3*333= 9*111= 27*37, демек берілген сан

999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінеді

ІІІ .Қортындылау Санның бөлінгіштік белгілері мен қасиеттерін еске түсіру

4.Үйге : Комбинаторикалық есептерді карау

Тақырыбы: Комбинаторикалық есептерді шешу. 17.10.18

Мақсаты: Комбинаторикалық есептерді есептерді жылдам, әрі тез шығара алады

Формасы: жеке, жұптық

Әдіс-тәсілдер: АКТ, СТО, «Диалогтік оқыту» әдістері

Пән аралық байланыс: математика

1.Сабақтың барысы:

2. Комбинаторикалық есептерді шешу.

Алмастырулар. Х жиыны n элементтен құралған жиын болсын. Онда Х жиынының элементтерінен құралған, ұзындығы k-ға тең және элементтері қайталанбайтын әрбір шеруді n – нен k бойынша алынған қайталанбайтын орналастыру деп аталады. Оны   арқылы белгілейді.
 немесе 
1-мысал: 4 оқушыны 7 орындыққа неше түрлі тәсілмен отырғызып шығуға болады?
Шешуі: Мұнда Х жиыны 7 элементтен тұрады. Онда бізге қажетті сан барлық 7-ден 4 бойынша қайталанбайтын орналастырулар санына тең. Өйткені бірнеше оқушы бір орындыққа отырмайды деп есептейміз.
Сонда  Жауабы:840
2-мысал: Бес адамды кезекке неше түрлі тәсілмен тұрғызуға болады?
Шешуі: Бізге қажетті сан 5 элементтен алынған барлық алмастырулар санына тең.



Жауабы: 120

3-мысал: Үш таңбалы саннан қанша әртүрлі цифрдан құрастырылған үш таңбалы сан алуға болады?

Жауабы: 6


Терулер. n элементі бар Х жиынының әрбір k элементі ішкі жиынын n – нен k бойынша алынған қайталанбайтын терулер деп атайды. 
 арқылы белгілейді.
4-мысал: Шахмат турниріне 12 ойыншы қатысты және әрбір шахматшы өзгелермен бір-бір ойыннан ойнайды. Турнирде барлығы неше партия ойналды?
Шешуі: Әрбір партияны өткізуге екі ойыншы қатысады. Онда барлық өткізілген партиялар саны 12-ден 2 бойынша алынған терулер санына тең.




3.Есептер шығару №1 Жәшікте 15 шар бар, оның 5 көк,10 қызыл; Қалай болса солай алты шар алынды. Осы шарлардың 2-і көк болу ықтималдығын тап.



Шешуі.№2 Қорапта 15 қызыл,9 көк,6 жасыл шар бар. Қалай болса солай 6 шар алынды. Осы шарлардың 1 жасыл,2 көк,3 қызыл болуының ықтималдығы қандай? Теру заңы бойынша: Жалпы жағдай



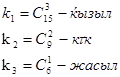
4 Үйге тапсырма

1.Л,Н,Р,Т әріптерінен тұратын 5 әріпті сөз алфавитті ретпен берілген. Тізбек басы мынандай:

1. ЛЛЛЛЛ 2. ЛЛЛЛН 3. ЛЛЛЛР 4. ЛЛЛЛТ 5. ЛЛЛНЛ

Тізімнің бас жағынан санағандағы 150-ші орында тұрған сөзді табыңдар.

2 тапсырма

М,С,Т,Ф әріптерінен тұратын 4 әріпті сөз алфавитті ретпен берілген. Тізбек басы мынандай:

1. ММММ 2. МММС 3. МММТ 4. МММФ 5. ММСМ
Тізімнің бас жағынан санағандағы 138-ші орында тұрған сөзді табыңдар.
3 тапсырма

В,Л,Т,У әріптерінен тұратын 4 әріпті сөз алфавитті ретпен берілген. Тізбек басы мынандай:

1. ВВВВ 2. ВВВЛ 3. ВВВТ 4. ВВВУ ……

75-ші орыннан кейінгі тұрған сөзі табыңдар

5.Қортындылау


Тақырыбы: Комбинаторикалық есептерді шешу. 19.10.18

Мақсаты: Комбинаторикалық есептерді есептерді жылдам, әрі тез шығара алады

Формасы: жеке, жұптық

Әдіс-тәсілдер: АКТ, СТО, «Диалогтік оқыту» әдістері

Пән аралық байланыс: математика

1.Сабақтың барысы:

2.Есеп шығару №1 Өрнекті ықшамдау:

№2

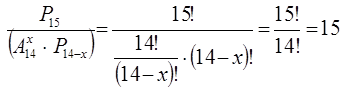
Жәшікте 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 цифрлары арқылы нөмірленген 10 бұйым бар. Кез келген үш бұйымды неше тәсілмен алуға болады?

Шешуі. Мұнда алынған бұйымдардың орналасу реті маңызды болмағандықтан теру формуласы бойынша

= тәсіл бар екенін көру қиын емес.

№3. Жәшікте 10 деталь бар. Оның алтауы стандартты деталь. Жәшіктен құрамында екі стандартты деталь болатындай бес детальды неше әдіспен алуға болады?

Шешуі. Есептің шартынан N=10, n=6, к=2, m=5. n=6 стандарттық детальдан к=2 стандарттық детальды әдіспен алуға болады, ал қалған үш деталь стандартты болмау керек. N-n=10-6=4 стандартты емес детальдан m-k=3 стандартты емес детальды әдіспен алуға болады. Сонымен, жәшіктен 5 детальды алу және оның ішінде 3 стандартты емес деталь болатынын көбейту ережесі бойынша табамыз. = әдіс болады.
№4 Шахмат турниріне 6 адам қатысқан.Әрқайсысы бір-бірімен 2 партия ойнаған. Неше партия ойналды?Бұл есепті нұсқалар кестесі арқылы шығаруға болады

I	II	III	IV	V	VI
I	—	+	+	+	+	+
II	—	—	+	+	+	+
III	—	—	—	+	+	+
IV	—	—	—	—	+	+
V	—	—	—	—	—	+
VI	—	—	—	—	—	—

Сонда” + „таңбасын санасақ 15 партия,ал бір-бірімен 2 партиядан 2*15=30 партия ойнаған.
Үйге Теңдеулер немесе теңдеулер жүйелерін құруға берілген есептерді шешу.

Тақырыбы: Теңдеулер немесе теңдеулер жүйелерін құруға берілген есептерді шешу. 26.10.18

Мақсаты: Теңдеулер немесе теңдеулер жүйелерін құруға берілген есептерді шешуеді

Формасы: жеке, жұптық

Әдіс-тәсілдер: АКТ, СТО, «Диалогтік оқыту» әдістері

Пән аралық байланыс: математика

1.Сабақтың барысы:

2. Теңдеулер немесе теңдеулер жүйелерін құруға берілген есептерді шешу.

1.а)Белгісізді таңдау.

Көп жағдайда есеп нені сұраса, соны белгісіз ретінде алуға болады.Бұл нұсқаны бірінші қарастыру керек, бірақ бұл ережені қатаң түрде сақтау қажет емес, кейде теңдеуді қарапайым түрде құрастыруға болады.Содан кейін ең соңғы жауап, есептің сұрауына қайта оралып, дұрыс жауап беру керек. Ең маңыздысы, белгісіздер саны, белгісіз неғұрлым көп болса, солғұрлым теңдеу құруға оңай болады, немесе теңсіздік құруға болады, бірақ оны шешу қиынырақ болады.Егер белгілі бір кірістірілген шамамен қарапайым түрде өрнектелетін болса, онда жаңа белгісізді енгізудің қажеті жоқ.

Ә).Теңдеу құру (мүмкін теңсіздік).

Теңдеулер жүйесін құру барысында есептің барлық шартын қолдану керек.Теңдеулер саны белгісіздер санымен бірдей болу керек.

В).Қажетті белгісізді немесе қажетті белгісіздер комбинациясын табу.

Егер шешім кезінде кейбір түбірді алып тастау қажет болса, онда оны есеп шартына байланысты қарастыру керек.

Сөз есептерді төмендегідей топтарға бөліп алған қолайлы.

қозғалысқа берілген есептер.

жұмысқа және еңбек өнімділігіне берілген есептер

ІІ. Есеп шығару

Бірінші бассейнде 1600 екінші бассейнде 1215 су бар. Бірінші бассейнді тазарту үшін одан сағатына 65 су насоспен сыртқа ағызылды. Екінші бассейнге сағатына 45 су насоспен құйылды. Екі насос жұмыстарын бір уақытта бастаса, онда неше сғаттан соң екі бассейндегі сулар теңеседі?

Шешуі:


Жауабы: 3,5 сағат


Тақырыбы: теңдеулер жүйелерін құруға берілген есептерді шешу.

07.11.18

Мақсаты: Теңдеулер немесе теңдеулер жүйелерін құруға берілген есептерді шешуеді