Файл: Цели и задачи дисциплины, ее место и роль в учебном процессе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 79
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определение ожидаемой доходности и дисперсии портфеля. Как установлено, ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле:
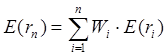
где
– вес каждой ценной бумаги в портфеле.
Подставим в эту формулу выражение
из формулы = + 
:
=
[ + ]Выделим в этом равенстве слагаемые, на которые не оказывает воздействие изменения рынка, и которые зависят от рыночных показателей:
=
+ ( ) Для придания этой формуле компактности, Шарп предложил считать рыночный портфель в качестве условной (n+1)-ой акции портфеля. В таком случае, второе слагаемое уравнения
= + ( ) можно представить в виде:(
)
=
( ),где:
= 
( ) =
При этом считается, что дисперсия (n+1)-ой ошибки равна дисперсии рыночной доходности:
= . Выражение = представляет собой сумму взвешенных величин «беты» ( ) каждой ценной бумаги (где весом служат ) и называется портфельной бетой ( ).С учетом выражений учетом выше сказанного формулу ожидаемой доходности портфеля можно записать так:
= 
Итак, ожидаемую доходность портфеля E(rn) можно представить состоящей из двух частей:
а) суммы взвешенных параметров каждой ценной бумаги – W11+W22+...+Wnn, что отражает вклад в E(rn) самих ценных бумаг, и
б) компоненты Wn+1n+1=(
) , то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.Дисперсия портфеля. Как известно, дисперсию портфеля можно представить в виде:
=
+ 
Если вместо значений и подставить сюда выражения:
= +
= ,
провести соответствующие вычисления и воспользоваться условиями (n+1) акции, то можно показать, что дисперсия портфеля представляется в виде:
=
При этом только необходимо иметь в виду, что Wn+1 =
, то есть (Wn+1) =(W11+W22+...+Wnn) , а 
= . Значит, дисперсию портфеля, содержащего n акций, можно представить состоящей из двух компонент:а) средневзвешенных дисперсий ошибок
, где весами служат , что отражает долю риска портфеля, связанного с риском самих ценных бумаг (собственный риск);б) – взвешенной величины дисперсии доходности рыночного портфеля , где весом служит квадрат портфельной беты, что отражает долю риска портфеля, определяемого нестабильностью самого рынка (рыночный риск).
Исходя из изложенного, можно аналогично тому, как это делалось в предыдущей части, показать, что с увеличением числа ценных бумаг в портфеле первая часть риска портфеля (
) будет стремиться к нулю. Поэтому диверсификация портфеля приводит к уменьшению риска, связанного с нестабильностью самих ценных бумаг, оставляя лишь компоненту , зависящую от нестабильности самого рынка.Формулирование цели инвестора в модели Шарпа. В модели Шарпа цель инвестора сводится к следующему:
необходимо найти минимальное значение дисперсии портфеля:
при следующих начальных условиях:
Отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:
1) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N лет, за который будут наблюдаться значения доходности каждой ценной бумаги.
2) По рыночному индексу (например, РТС) вычислить рыночные доходности для того же промежутка времени.
3) Найти величины и :
=
4) Вычислить дисперсии ошибок регрессионной модели.
5) Решить с применением методов линейной алгебры задачу построения границы эффективных портфелей.
Рассмотрим пример построения границы эффективных портфелей, состоящих из акций «А», «В» и «С». Итак, задача инвестора в этом случае сводится к следующему: необходимо минимизировать выражение:
при следующих начальных условиях:
Подставим вычисленные ранее значения , ,
, 
и 
в эти выражения:
Для нахождения весов ценных бумаг необходимо предварительно составить полином Лагранжа:
,где
Г1, Г2, Г3 – множители Лагранжа.
Затем берутся 7 частных производные полинома L по каждой из семи неизвестных W1, W2, W3, W4, а также Г1, Г2, Г3 и приравниваются к нулю:
= 0,0146Wa + 0,2494Г1 + Г2 - 0,9787Г3 = 0
= 0,0271Wb - 0,0117Г1 + Г2 + 0,9470Г3 = 0
= 0,0756Wc + 0,1165Г1 + Г2 + 0,5256Г3 = 0
= 0,0156W4 + 0,1475Г1 - Г3 = 0
= 0,2494Wa - 0,0117Wb + 0,1165Wc + 0,1475W4 - * =0
= Wa + Wb + Wc = 0
= -0,9787Wa + 0,9470Wb + 0,5256Wc - W4 = 0В матричной форме эти семь уравнений записываются в виде:
Представим это в виде матричного уравнения: