Файл: Цели и задачи дисциплины, ее место и роль в учебном процессе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 82
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
А ,WВ ,WС :
WА = -6,82337E* + 1,344214
WВ = -5,9503E* + 1,126742
WС = + 12,77367E* - 1,47096
Задавая различные значения E* и вычисляя каждый раз по формулам, представленным выше, величины Wi, можно таким образом найти эффективные портфели и определить в каждом случае их дисперсии и стандартные отклонения.
Ниже в таблице 6 приведены значения ожидаемой доходности и стандартного отклонения для эффективных портфелей, составленных из акций компаний.
Таблица 6.
Ожидаемые доходности и стандартные отклонения для различных эффективных портфелей
Если перенести вычисленные значения ожидаемой доходности и стандартного отклонения эффективных портфелей, сформированные на основе акций компаний «А», «В» и «С», на координатную плоскость, обвести полученные точки, то получим линию – границу эффективных портфелей (рис. 9):
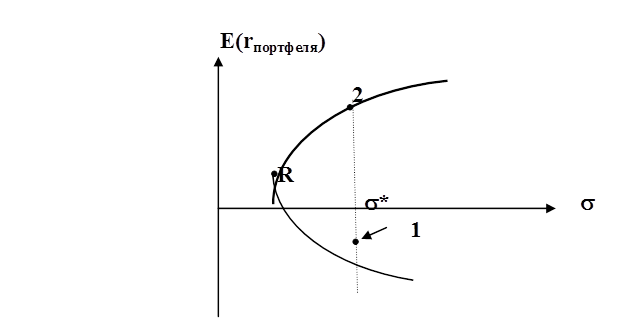
Рис. 9. Граница эффективных портфелей в соответствии в полученными данными
Как видно из рисунка 9, заданной величине риска портфеля, положим, * соответствуют два эффективных портфеля 1 и 2. Однако, согласно теореме Г. Марковица, инвестор должен предпочесть портфель 2. Аналогично инвестор поступит и при иных величинах портфеля. Тогда очевидно, что инвестору вообще не имеет смысла строить нижнюю ветвь границы эффективных портфелей (ГЭП), расположенную ниже точки R. Портфель R соответствует портфелю с минимальной дисперсией (MVP). В этой связи при построении ГЭП рекомендуется предварительно вычислить характеристики MVP, а затем при вычислении величин весов акций подставлять Е*≥ E(rMVP). На рисунке граница эффективных портфелей проходит через точку MVP, соответствующую портфелю с минимальной дисперсией.
Находить веса MVP можно следующим способом: в исходной матрице Т вычеркнуть строку и столбец, соответствующие ограничению Е* (в нашем случае это четвертая строка и четвертый столбец), и для полученной матрицы (Т – 1) найти матрицу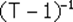 , обратную матрице (T - 1). Коэффициенты в первых трех строках последнего столбца этой обратной матрицы составят веса портфеля с минимальной дисперсией. Для акций компаний «А», «В» и «С» эти веса будут равны: WА = 0,5195; WВ = 0,4077; WС = 0,0727.
, обратную матрице (T - 1). Коэффициенты в первых трех строках последнего столбца этой обратной матрицы составят веса портфеля с минимальной дисперсией. Для акций компаний «А», «В» и «С» эти веса будут равны: WА = 0,5195; WВ = 0,4077; WС = 0,0727.
Нахождение оптимального портфеля. Как отмечалось, в теории Марковица инвесторы стремятся сформировать портфель ценных бумаг, чтобы максимизировать получаемую полезность. Иными словами, каждый инвестор желает таким образом сформировать портфель, чтобы сочетание ожидаемой доходности и уровня риска
и уровня риска 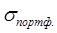
портфеля приносило ему максимальное удовлетворение потребностей и минимизировало риск при желаемой доходности. Разные инвесторы имеют отличные друг от друга мнения об оптимальности сочетания и
и  , поскольку отношение одного инвестора к риску не похоже на желание рисковать другого инвестора. Поэтому, говоря об оптимальном портфеле, надо иметь в виду, что эта категория сугубо индивидуальна, и оптимальные портфели разных инвесторов теоретически отличаются друг от друга. Тем не менее каждый оптимальный портфель непременно является эффективным, то есть инвесторы выбирают удовлетворяющий их (оптимальный) портфель из эффективных портфелей.
, поскольку отношение одного инвестора к риску не похоже на желание рисковать другого инвестора. Поэтому, говоря об оптимальном портфеле, надо иметь в виду, что эта категория сугубо индивидуальна, и оптимальные портфели разных инвесторов теоретически отличаются друг от друга. Тем не менее каждый оптимальный портфель непременно является эффективным, то есть инвесторы выбирают удовлетворяющий их (оптимальный) портфель из эффективных портфелей.
Метод определения оптимального портфеля основывается на совмещении объективно полученной границы эффективных портфелей и субъективной оценки отдельным инвестором полезности того или иного портфеля, то есть той или иной комбинации и
и  . Построив границу эффективных портфелей, инвестор должен задать сам себе вопрос какую доходность он ожидает от портфеля? Предположим, что таковой является
. Построив границу эффективных портфелей, инвестор должен задать сам себе вопрос какую доходность он ожидает от портфеля? Предположим, что таковой является  = 0,15. После этого по кривой границы эффективных портфелей он определяет уровень риска такого портфеля:
= 0,15. После этого по кривой границы эффективных портфелей он определяет уровень риска такого портфеля:  =0,0857. Затем инвестор должен оценить, удовлетворяет ли его такой уровень риска. Если инвестор готов к более высокому уровню риска, то ему целесообразно выбрать портфель с
=0,0857. Затем инвестор должен оценить, удовлетворяет ли его такой уровень риска. Если инвестор готов к более высокому уровню риска, то ему целесообразно выбрать портфель с  =0,16 и
=0,16 и  =0,1081. Тот портфель, который при установленной инвестором доходности
=0,1081. Тот портфель, который при установленной инвестором доходности 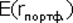
даст наилучшее сочетание и
и  , будет оптимальным.
, будет оптимальным.
Вопрос 2. Оптимизация инвестиционного портфеля в соответствии с теорией Шарпа.
Выведенные Марковицем правила построения границы эффективных портфелей позволяет находить оптимальный (с точки зрения инвестора) портфель для любого количества ценных бумаг в портфеле. Основной сложностью применения метода Марковица является большой объем вычислений, необходимый для определения весов Wi каждой ценной бумаги. Действительно, если портфель объединяет n ценных бумаг, то для построения границы эффективных портфелей необходимо предварительно вычислить n значений ожидаемых (средних арифметических) доходностей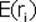 каждой ценной бумаги, n величин дисперсий всех доходностей и n(n-1)/2 выражений ковариаций акций в портфеле. При увеличении числа ценных бумаг в портфеле, количество необходимых значений ковариаций становится непомерно большим. Например, при 100 ценных бумаг в портфеле необходимое количество исходных данных превысит 5000.
каждой ценной бумаги, n величин дисперсий всех доходностей и n(n-1)/2 выражений ковариаций акций в портфеле. При увеличении числа ценных бумаг в портфеле, количество необходимых значений ковариаций становится непомерно большим. Например, при 100 ценных бумаг в портфеле необходимое количество исходных данных превысит 5000.
В 1963 году американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений.
Общее описание модели У. Шарпа. В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две случайные зависимые переменные величины X и Y линейным выражением типа:
Y = + X
В модели Шарпа переменной Х считается величина какого-то рыночного показателя. Сам Шарп в качестве такой переменной рассматривал доходность рыночного портфеля . В качестве переменной Y берется отдача какой-то i-ой акции портфеля. Представленное выше уравнение называется уравнением линейной регрессии, а коэффициенты и считаются параметрами линейной регрессии.
Если задана длительность холдингового периода и известны значения индекса (например, РТС) I в начале Iначальн.и в конце Iконечен.холдингового периода, то доходность рыночного портфеля за этот период находится по формуле:
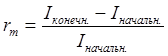
Построение регрессионной модели. Предположим, что портфель формируется из рассмотренных ранее акций фирм «А», «В» и «С». Пусть задана длительность будущего холдингового периода (для последующего сравнения модели Шарпа с моделью Марковица будем полагать, что эта длительность совпадает с выбираемой длительностью в модели Марковица) и заданы N = 10 шагов расчета в прошлом. На основании данных об изменениях рыночного индекса вычислим доходность рыночного портфеля за N шагов расчета. Полученные данные внесем в табл. 7, где также приведены доходности акции С, вычисленные ранее:
Таблица 7.
Условные доходности рыночного портфеля и акции С
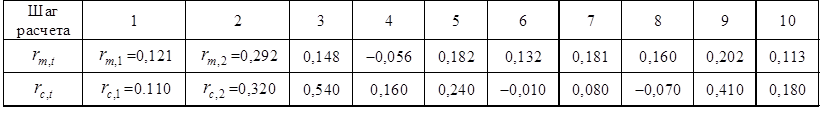
В таком случае для акции С уравнение линейной регрессии должно принимать вид:
=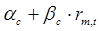
Ниже будут вычислены параметры линейной регрессии для акции С: =0,1165 и =0,5255. Значит, для этой акции уравнение линейной регрессии должно иметь вид:
= 0,1165 + 0,5256
Сравним получаемые по этой формуле теоретические величины и реально наблюдаемые значения , приведенные в табл. 7:
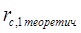 = 0,1165 + 0,5256× = 0,1165 + 0,5256×0,121 = 0,1802,
= 0,1165 + 0,5256× = 0,1165 + 0,5256×0,121 = 0,1802,
что отличается от наблюдаемого значения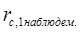 = 0,110. Чтобы уровнять теоретическую и реальную величины, необходимо провести коррекцию теоретической величины
= 0,110. Чтобы уровнять теоретическую и реальную величины, необходимо провести коррекцию теоретической величины  . Достигается это путем добавления к значению
. Достигается это путем добавления к значению  ошибки = 0,0702: (0,1802 0,0702 = 0,110).
ошибки = 0,0702: (0,1802 0,0702 = 0,110).
Поскольку величины и случайные, то, скорее всего, и остальные теоретические значения , получаемые с использованием уравнения линейной регрессии, будут отличаться от реально наблюдаемых величин , приведенных в таблице 7. В этой связи величины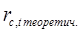 необходимо корректировать ошибкой на каждом шаге расчета. Так как величины и случайные, то и значения ошибки также должны представлять собой случайные величины. В итоге уравнение линейной регрессии для акции
необходимо корректировать ошибкой на каждом шаге расчета. Так как величины и случайные, то и значения ошибки также должны представлять собой случайные величины. В итоге уравнение линейной регрессии для акции
WА = -6,82337E* + 1,344214
WВ = -5,9503E* + 1,126742
WС = + 12,77367E* - 1,47096
Задавая различные значения E* и вычисляя каждый раз по формулам, представленным выше, величины Wi, можно таким образом найти эффективные портфели и определить в каждом случае их дисперсии и стандартные отклонения.
Ниже в таблице 6 приведены значения ожидаемой доходности и стандартного отклонения для эффективных портфелей, составленных из акций компаний.
Таблица 6.
Ожидаемые доходности и стандартные отклонения для различных эффективных портфелей
| Ожидаемая доходность портфеля | 0,1208 | 0,1300 | 0,1400 | 0,1500 | 0,1600 | 0,1700 | 0,1940 |
| Стандартное отклонение | 0,0440 | 0,0500 | 0,0654 | 0,0857 | 0,1081 | 0,1316 | 0,1894 |
Если перенести вычисленные значения ожидаемой доходности и стандартного отклонения эффективных портфелей, сформированные на основе акций компаний «А», «В» и «С», на координатную плоскость, обвести полученные точки, то получим линию – границу эффективных портфелей (рис. 9):
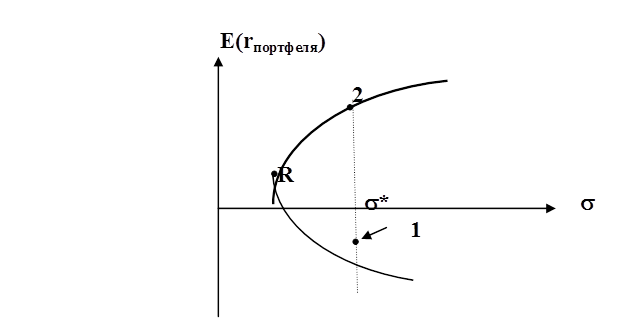
Рис. 9. Граница эффективных портфелей в соответствии в полученными данными
Как видно из рисунка 9, заданной величине риска портфеля, положим, * соответствуют два эффективных портфеля 1 и 2. Однако, согласно теореме Г. Марковица, инвестор должен предпочесть портфель 2. Аналогично инвестор поступит и при иных величинах портфеля. Тогда очевидно, что инвестору вообще не имеет смысла строить нижнюю ветвь границы эффективных портфелей (ГЭП), расположенную ниже точки R. Портфель R соответствует портфелю с минимальной дисперсией (MVP). В этой связи при построении ГЭП рекомендуется предварительно вычислить характеристики MVP, а затем при вычислении величин весов акций подставлять Е*≥ E(rMVP). На рисунке граница эффективных портфелей проходит через точку MVP, соответствующую портфелю с минимальной дисперсией.
Находить веса MVP можно следующим способом: в исходной матрице Т вычеркнуть строку и столбец, соответствующие ограничению Е* (в нашем случае это четвертая строка и четвертый столбец), и для полученной матрицы (Т – 1) найти матрицу
Нахождение оптимального портфеля. Как отмечалось, в теории Марковица инвесторы стремятся сформировать портфель ценных бумаг, чтобы максимизировать получаемую полезность. Иными словами, каждый инвестор желает таким образом сформировать портфель, чтобы сочетание ожидаемой доходности
портфеля приносило ему максимальное удовлетворение потребностей и минимизировало риск при желаемой доходности. Разные инвесторы имеют отличные друг от друга мнения об оптимальности сочетания
Метод определения оптимального портфеля основывается на совмещении объективно полученной границы эффективных портфелей и субъективной оценки отдельным инвестором полезности того или иного портфеля, то есть той или иной комбинации
даст наилучшее сочетание
Вопрос 2. Оптимизация инвестиционного портфеля в соответствии с теорией Шарпа.
Выведенные Марковицем правила построения границы эффективных портфелей позволяет находить оптимальный (с точки зрения инвестора) портфель для любого количества ценных бумаг в портфеле. Основной сложностью применения метода Марковица является большой объем вычислений, необходимый для определения весов Wi каждой ценной бумаги. Действительно, если портфель объединяет n ценных бумаг, то для построения границы эффективных портфелей необходимо предварительно вычислить n значений ожидаемых (средних арифметических) доходностей
В 1963 году американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений.
Общее описание модели У. Шарпа. В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две случайные зависимые переменные величины X и Y линейным выражением типа:
Y = + X
В модели Шарпа переменной Х считается величина какого-то рыночного показателя. Сам Шарп в качестве такой переменной рассматривал доходность рыночного портфеля . В качестве переменной Y берется отдача какой-то i-ой акции портфеля. Представленное выше уравнение называется уравнением линейной регрессии, а коэффициенты и считаются параметрами линейной регрессии.
Если задана длительность холдингового периода и известны значения индекса (например, РТС) I в начале Iначальн.и в конце Iконечен.холдингового периода, то доходность рыночного портфеля за этот период находится по формуле:
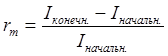
Построение регрессионной модели. Предположим, что портфель формируется из рассмотренных ранее акций фирм «А», «В» и «С». Пусть задана длительность будущего холдингового периода (для последующего сравнения модели Шарпа с моделью Марковица будем полагать, что эта длительность совпадает с выбираемой длительностью в модели Марковица) и заданы N = 10 шагов расчета в прошлом. На основании данных об изменениях рыночного индекса вычислим доходность рыночного портфеля за N шагов расчета. Полученные данные внесем в табл. 7, где также приведены доходности акции С, вычисленные ранее:
Таблица 7.
Условные доходности рыночного портфеля и акции С
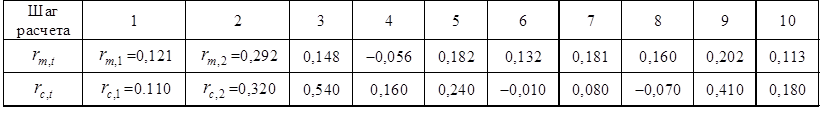
В таком случае для акции С уравнение линейной регрессии должно принимать вид:
=
Ниже будут вычислены параметры линейной регрессии для акции С: =0,1165 и =0,5255. Значит, для этой акции уравнение линейной регрессии должно иметь вид:
= 0,1165 + 0,5256
Сравним получаемые по этой формуле теоретические величины и реально наблюдаемые значения , приведенные в табл. 7:
что отличается от наблюдаемого значения
Поскольку величины и случайные, то, скорее всего, и остальные теоретические значения , получаемые с использованием уравнения линейной регрессии, будут отличаться от реально наблюдаемых величин , приведенных в таблице 7. В этой связи величины

