Файл: Цели и задачи дисциплины, ее место и роль в учебном процессе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 81
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
С должно иметь следующий вид:
= + ,
+ ,
где:
– случайная ошибка.
В общем случае, если в портфель включено nакций, то для любой i-ой акции портфеля уравнение линейной регрессии выглядит следующим образом:
= ,
,
где:
– доходность i-ой акции портфеля за шаг t;
– параметр регрессии, называемый коэффициентом «альфа»; показывает, какая часть доходности i-ой акции портфеля не связана с изменениями доходности рыночного портфеля ;
– параметр линейной регрессии, называемый коэффициентом «бета», показывающий чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности ;
– доходность рыночного портфеля в момент t;
– случайная ошибка, свидетельствующая о том, что реальные, действующие значения и отклоняются от линейной зависимости.
Уравнение = является основным в линейном регрессионном анализе и берется за основу в модели Шарпа. В линейном регрессионном анализе полагается, что средняя арифметическая (ожидаемая) величина ошибок наблюдения E( )=0, то есть фактические величины в среднем равномерно распределяются выше и ниже значений, получаемых при линейной регрессии.
является основным в линейном регрессионном анализе и берется за основу в модели Шарпа. В линейном регрессионном анализе полагается, что средняя арифметическая (ожидаемая) величина ошибок наблюдения E( )=0, то есть фактические величины в среднем равномерно распределяются выше и ниже значений, получаемых при линейной регрессии.
Параметр бета. Особое значение необходимо уделить параметру , поскольку он определяет чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности. Коэффициент для каждой ценной бумаги показывает, на сколько процентов изменится доля , определяемая воздействием рынка ( × ), при изменении рыночной доходности на 1%.
В общем случае, если >1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность rm. Соответственно, при <1 ценная бумага имеет меньший размах отклонений доходностей rj от средней арифметической (ожидаемой) величины
E(ri), чем рыночная доходность. В этой связи ценные бумаги с коэффициентом >1 классифицируются как более рискованные, чем рынок в целом, а с <1 - менее рискованными, чем рынок в целом.
Как показывают исследования, для большинства ценных бумаг коэффициент >0, хотя могут встретиться ценные бумаги и с отрицательной величиной . В последнем случае доходности этих ценных бумаг отрицательно коррелированны с доходностью рыночного портфеля. Следует учитывать, что и в случае отрицательных величин , если величина этого коэффициента по модулю превосходит единицу, то есть (например, = 1,5), то акции считаются более рискованными, чем рынок в целом.
Поскольку коэффициент характеризует зависимость доходности исследуемой акции и рыночного портфеля, то, очевидно, что данный коэффициент отражает только систематическую, недиверсифицируемую часть риска.
Определение параметров и регрессионной модели и оценка результатов регрессии. Для нахождения параметров и по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров и берутся такие значения, которые минимизируют сумму квадратов ошибок , то есть которых величина:
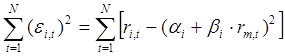
достигает минимума. Если провести необходимые вычисления, то окажется, что выражение имеет минимум, когда параметры и принимают следующие значения:
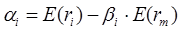
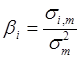
Если будут известны наблюдаемые в течение N лет величины и , то, пользуясь известными формулами для вычисления ожидаемых доходностей, ковариаций и дисперсий, можно найти E(ri), E(rm), и , подставить их в выше представленные формулы и вычислить параметры регрессии и .
Найдем значения коэффициентов и для акций «А», «В» и «С»:
=0,2494 и = 0,9787
= 0,0117 и =0,9470
= 0,1165 и = 0,5256
Вычисление дисперсий случайной ошибки. Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значения
дисперсий случайных ошибок, то проведем необходимые вычисления. Общая формула для вычисления дисперсии случайной ошибки имеет вид:
=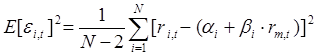
Для акций «А» вычисления дают:
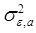 =[(0,1200,2694+0,97870,1212) +(0,0400,2694+0,97870,2924) +(0,0100,2694+0,97870,1479) + и т.д. по всем 10 годам] / 8 = 0,0073
=[(0,1200,2694+0,97870,1212) +(0,0400,2694+0,97870,2924) +(0,0100,2694+0,97870,1479) + и т.д. по всем 10 годам] / 8 = 0,0073
Соответственно: =0,0136 и =0,0375.
=0,0136 и =0,0375.
Для наглядности сведем данные регрессионного анализа для акций «А», «В» и «С» в одну таблицу (табл. 8):
Таблица 8.
Данные, полученные с использованием регрессионной модели

*) Вычислены ранее без регрессионных формул
Оценка результатов регрессии. Вычисленные параметры и регрессионной модели дают представление об общих тенденциях взаимосвязей между изменениями доходности рыночного портфеля и доходностью оцениваемой акции. Однако величины и не позволяют давать однозначный ответ о степени подобной взаимосвязи. Точность регрессионной модели, степень взаимосвязи и определяется разбросом случайных ошибок , который можно оценить с помощью дисперсии случайной ошибки . Кроме того, точность регрессии можно определить, оценивая, сколь точно регрессионная модель определяет дисперсию доходности ценных бумаг, для которых составляется регрессионная модель.
Чуть ниже будет показано, что дисперсию i-ой ценной бумаги можно представить в виде двух слагаемых:
=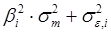
Как видим, первое слагаемое свидетельствует, что часть риска i-ой ценной бумаги определяется нестабильностью самого рынка, поскольку туда входит – дисперсия рыночной доходности rm. Второе же слагаемое показывает, что в суммарном риске ценной бумаги присутствует и собственная доля, не зависящая от колебаний рынка.
Разделим обе части равенства =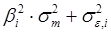 на величину :
на величину :

Обратим внимание, что в этом случае первое слагаемое будет показывать, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели = , а второе слагаемое – степень неточности регрессионной модели. Значит, чем ближе величина
, а второе слагаемое – степень неточности регрессионной модели. Значит, чем ближе величина 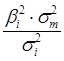 к единице, тем более точная регрессионная модель.
к единице, тем более точная регрессионная модель.
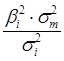 – это квадрат коэффициента корреляции
– это квадрат коэффициента корреляции 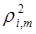 . Именно квадрат коэффициента корреляции
. Именно квадрат коэффициента корреляции 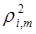 является мерой оценки точности линейной регрессии, то есть мерой того, насколько точно уравнение регрессии подходит для описания соотношений реальных данных и .
является мерой оценки точности линейной регрессии, то есть мерой того, насколько точно уравнение регрессии подходит для описания соотношений реальных данных и .
Вычислим величину для акций «А», «В» и «С», вспомнив ранее вычисленные значения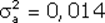 ;
;  ;
;  :
:
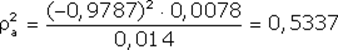
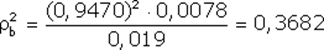
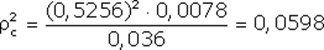
Эти данные свидетельствуют, что лучше всего линейная регрессия описывает поведение акций компании «А», так как величина ближе к единице, чем для других компаний. Для компании «С» использование выбранного индекса РЦБ при составлении линейной регрессионной модели не оправданно, так как только 6% (0,0598) изменений ее доходности можно связать с колебаниями рынка.
Использование модели Шарпа для построения границы эффективных портфелей.
В основу модели Шарпа положена линейная регрессия. Для применения модели Шарпа необходимо предварительно ввести ряд условий. Если предположить, что инвестор формирует портфель из
n ценных бумаг, то будем считать, что:
1) Средняя арифметическая (ожидаемая) величина случайных ошибок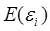 = 0 для всех акций портфеля, то есть для i=1,2,...,n.
= 0 для всех акций портфеля, то есть для i=1,2,...,n.
2) Дисперсия случайных ошибок для каждой ценной бумаги постоянна.
3) Для каждой акции портфеля отсутствует корреляция между наблюдаемыми в течение N шагов расчета величинами случайных ошибок, то есть E[ ]= 0 (t=1,2,...,N).
4) Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, иначе говоря, E[ ]=0.
5) Отсутствует корреляция между случайными ошибками и рыночной доходности, то есть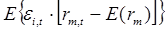 = 0.
= 0.
Определение доходности и риска отдельной акции портфеля. Используя эти упрощения, можно получить выражения E(ri), и i,j для любых акций в портфеле:
 = +
= + 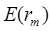
= +
=
необходимые для построения границы эффективных портфелей. При этом инвестору требуется предварительно вычислить n значений , n величин , n значений , а также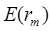 и . Следовательно, всего потребуется найти: (n+n+n+2)=3n+2 начальных данных, что существенно меньше объема вычислений для модели Марковица. Например, при формировании портфеля из 30 ценных бумаг для определения границы эффективных портфелей надо 3×30+2=92 начальных данных по модели Шарпа и 495 (в 5 раз больше!) по модели Марковица.
и . Следовательно, всего потребуется найти: (n+n+n+2)=3n+2 начальных данных, что существенно меньше объема вычислений для модели Марковица. Например, при формировании портфеля из 30 ценных бумаг для определения границы эффективных портфелей надо 3×30+2=92 начальных данных по модели Шарпа и 495 (в 5 раз больше!) по модели Марковица.
Сокращение объема вычислений в модели Шарпа происходит потому, что все парные ковариации между доходностями ценных бумаг в портфеле предполагаются равными нулю. А чтобы отразить взаимное влияние риска одной ценной бумаги на риск другой ценной бумаги, Шарп предложил свести эти ковариационные эффекты к взаимосвязи ценных бумаг портфеля с каким-то рыночным индексом, например, S&P500. Иначе говоря, корреляция между доходностями ценных бумаг в портфеле выражается с помощью рыночного индекса.
=
где:
– случайная ошибка.
В общем случае, если в портфель включено nакций, то для любой i-ой акции портфеля уравнение линейной регрессии выглядит следующим образом:
=
где:
– доходность i-ой акции портфеля за шаг t;
– параметр регрессии, называемый коэффициентом «альфа»; показывает, какая часть доходности i-ой акции портфеля не связана с изменениями доходности рыночного портфеля ;
– параметр линейной регрессии, называемый коэффициентом «бета», показывающий чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности ;
– доходность рыночного портфеля в момент t;
– случайная ошибка, свидетельствующая о том, что реальные, действующие значения и отклоняются от линейной зависимости.
Уравнение =
Параметр бета. Особое значение необходимо уделить параметру , поскольку он определяет чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности. Коэффициент для каждой ценной бумаги показывает, на сколько процентов изменится доля , определяемая воздействием рынка ( × ), при изменении рыночной доходности на 1%.
В общем случае, если >1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность rm. Соответственно, при <1 ценная бумага имеет меньший размах отклонений доходностей rj от средней арифметической (ожидаемой) величины
E(ri), чем рыночная доходность. В этой связи ценные бумаги с коэффициентом >1 классифицируются как более рискованные, чем рынок в целом, а с <1 - менее рискованными, чем рынок в целом.
Как показывают исследования, для большинства ценных бумаг коэффициент >0, хотя могут встретиться ценные бумаги и с отрицательной величиной . В последнем случае доходности этих ценных бумаг отрицательно коррелированны с доходностью рыночного портфеля. Следует учитывать, что и в случае отрицательных величин , если величина этого коэффициента по модулю превосходит единицу, то есть (например, = 1,5), то акции считаются более рискованными, чем рынок в целом.
Поскольку коэффициент характеризует зависимость доходности исследуемой акции и рыночного портфеля, то, очевидно, что данный коэффициент отражает только систематическую, недиверсифицируемую часть риска.
Определение параметров и регрессионной модели и оценка результатов регрессии. Для нахождения параметров и по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров и берутся такие значения, которые минимизируют сумму квадратов ошибок , то есть которых величина:
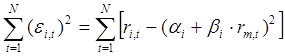
достигает минимума. Если провести необходимые вычисления, то окажется, что выражение имеет минимум, когда параметры и принимают следующие значения:
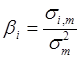
Если будут известны наблюдаемые в течение N лет величины и , то, пользуясь известными формулами для вычисления ожидаемых доходностей, ковариаций и дисперсий, можно найти E(ri), E(rm), и , подставить их в выше представленные формулы и вычислить параметры регрессии и .
Найдем значения коэффициентов и для акций «А», «В» и «С»:
=0,2494 и = 0,9787
= 0,0117 и =0,9470
= 0,1165 и = 0,5256
Вычисление дисперсий случайной ошибки. Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значения
дисперсий случайных ошибок, то проведем необходимые вычисления. Общая формула для вычисления дисперсии случайной ошибки имеет вид:
=
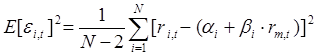
Для акций «А» вычисления дают:
Соответственно:
Для наглядности сведем данные регрессионного анализа для акций «А», «В» и «С» в одну таблицу (табл. 8):
Таблица 8.
Данные, полученные с использованием регрессионной модели

*) Вычислены ранее без регрессионных формул
Оценка результатов регрессии. Вычисленные параметры и регрессионной модели дают представление об общих тенденциях взаимосвязей между изменениями доходности рыночного портфеля и доходностью оцениваемой акции. Однако величины и не позволяют давать однозначный ответ о степени подобной взаимосвязи. Точность регрессионной модели, степень взаимосвязи и определяется разбросом случайных ошибок , который можно оценить с помощью дисперсии случайной ошибки . Кроме того, точность регрессии можно определить, оценивая, сколь точно регрессионная модель определяет дисперсию доходности ценных бумаг, для которых составляется регрессионная модель.
Чуть ниже будет показано, что дисперсию i-ой ценной бумаги можно представить в виде двух слагаемых:
=
Как видим, первое слагаемое свидетельствует, что часть риска i-ой ценной бумаги определяется нестабильностью самого рынка, поскольку туда входит – дисперсия рыночной доходности rm. Второе же слагаемое показывает, что в суммарном риске ценной бумаги присутствует и собственная доля, не зависящая от колебаний рынка.
Разделим обе части равенства =

Обратим внимание, что в этом случае первое слагаемое будет показывать, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели =
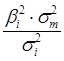 к единице, тем более точная регрессионная модель.
к единице, тем более точная регрессионная модель.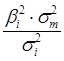 – это квадрат коэффициента корреляции
– это квадрат коэффициента корреляции Вычислим величину для акций «А», «В» и «С», вспомнив ранее вычисленные значения
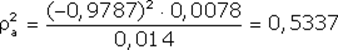
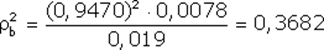
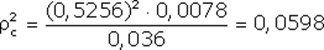
Эти данные свидетельствуют, что лучше всего линейная регрессия описывает поведение акций компании «А», так как величина ближе к единице, чем для других компаний. Для компании «С» использование выбранного индекса РЦБ при составлении линейной регрессионной модели не оправданно, так как только 6% (0,0598) изменений ее доходности можно связать с колебаниями рынка.
Использование модели Шарпа для построения границы эффективных портфелей.
В основу модели Шарпа положена линейная регрессия. Для применения модели Шарпа необходимо предварительно ввести ряд условий. Если предположить, что инвестор формирует портфель из
n ценных бумаг, то будем считать, что:
1) Средняя арифметическая (ожидаемая) величина случайных ошибок
2) Дисперсия случайных ошибок для каждой ценной бумаги постоянна.
3) Для каждой акции портфеля отсутствует корреляция между наблюдаемыми в течение N шагов расчета величинами случайных ошибок, то есть E[ ]= 0 (t=1,2,...,N).
4) Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, иначе говоря, E[ ]=0.
5) Отсутствует корреляция между случайными ошибками и рыночной доходности, то есть
Определение доходности и риска отдельной акции портфеля. Используя эти упрощения, можно получить выражения E(ri), и i,j для любых акций в портфеле:
= +
=
необходимые для построения границы эффективных портфелей. При этом инвестору требуется предварительно вычислить n значений , n величин , n значений , а также
Сокращение объема вычислений в модели Шарпа происходит потому, что все парные ковариации между доходностями ценных бумаг в портфеле предполагаются равными нулю. А чтобы отразить взаимное влияние риска одной ценной бумаги на риск другой ценной бумаги, Шарп предложил свести эти ковариационные эффекты к взаимосвязи ценных бумаг портфеля с каким-то рыночным индексом, например, S&P500. Иначе говоря, корреляция между доходностями ценных бумаг в портфеле выражается с помощью рыночного индекса.

