Министерство науки и высшего образования Российской Федерации

федеральное государственное автономное образовательное учреждение

высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Институт судостроения и морской арктической техники (Севмашвтуз)

(наименование высшей школы/ филиала/ института/ колледжа)

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

По дисциплине: математика

На тему: Линейная алгебра и аналитическая геометрия

Выполнила обучающаяся:

Кудрявцева София Сергеевна

(ФИО)

Направление подготовки / специальность:

15. 03. 05. Конструкторско – технологическое обеспечение машиностроительных производств

(код и наименование)

Курс:1

Группа:523227

Руководитель: Зулукаева Ольга Вадимовна

(ФИО руководителя)

Отметка о зачете

(отметка прописью)

(дата)

Руководитель

Зулукаева О.В.

(подпись руководителя)

(инициалы, фамилия)

Северодвинск 2022

---

ЛИСТ ЗАМЕЧАНИЙ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова» филиал в г. Северодвинске Архангельской области

ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ

По математике

(наименование дисциплины)

студенту ИСМАРТ курса 1 группы 523227

Кудрявцевой Софии Сергеевны

(фамилия, имя, отчество студента)

15.03.05 Конструкторско-технологическое обеспечение машиностроительных производств

(код и наименование направления подготовки/специальность )

ТЕМА: Линейная алгебра и аналитическая геометрия

ИСХОДНЫЕ ДАННЫЕ. Вариант №17

Часть I

Задание 1. Вычислить произведение матриц:



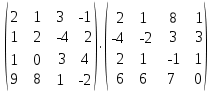
Задание 2. Вычислить определитель:



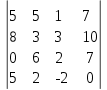
Задание 3. Найти обратную матрицу для матрицы А:

А=

Задание 4. Решить системы уравнений

а) Методом обратной матрицы:

б) методом Крамера:

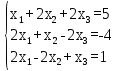
в) методом Гаусса:

Часть II.

Задание 1. Написать разложение вектора ⃗а по базису ⃗ , ⃗

⃗а = (1,4), ⃗ = (1,3), ⃗ = (-2,-3) .

Задание 2. Установить, являются ли векторы 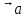, ⃗???? , ⃗???? линейно-зависимыми:

⃗???? = (2,5,1) , ⃗????= (3,-2,1) , ⃗???? =(2,4,1).

Задание 3. Найдите площадь параллелограмма построенного на векторах ⃗???? и ????⃗ :

⃗???? =(1,3,2), ⃗???? =(1,2,2).

---

Задание 4. От общего уравнения прямой перейти к каноническому, параметрическому и с угловым коэффициентом уравнениям прямой:

3x-2y+6=0.

Задание 5. Написать уравнение плоскости, проходящей через три заданные точки :

М₁(2,1,1), М₂=(1,2,1), М₃(1,1,2).

Задание 6. От общего уравнения прямой перейти к каноническому уравнению:



Задание 7. Найти угол между прямыми:

L₁:x+y-1=0, L₂: 2x-2y+1=0.

Задание 8. Найдите расстояние от точки М до плоскости Р:

М(2,-3,-4), Р:x-y+2z-1=0

Задание 9. Найти проекцию точки М на плоскость Р

М(2,1,-1), Р:2x-y-3z-1=0

Задание 10. Составить уравнение эллипса, зная его большую полуось а и фокусы F1, F2: a=6, F₁(-2,-1), F₂(6,-1)
ЧАСТЬ 1

Задание 1. Вычислить произведение матриц:



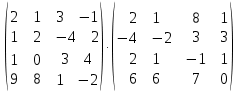
Решение:

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пусть даны две матрицы:

А= 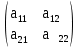и В=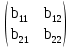 , тогда по формуле:
С=А*B= 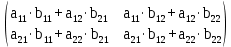(1)
Найдем произведение матриц: =

= ,

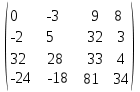Компоненты матрицы С вычисляются следующим образом:

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ + a₁₃ · b₃₁ + a₁₄ · b₄₁ = 2 · 2 + 1 · (-4) + 3 · 2 + (-1) · 6 = 4 - 4 + 6 - 6 = 0
c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ + a₁₃ · b₃₂ + a₁₄ · b₄₂ = 2 · 1 + 1 · (-2) + 3 · 1 + (-1) · 6 = 2 - 2 + 3 - 6 = -3
c₁₃ = a₁₁ · b₁₃ + a₁₂ · b₂₃ + a₁₃ · b₃₃ + a₁₄ · b₄₃ = 2 · 8 + 1 · 3 + 3 · (-1) + (-1) · 7 = 16 + 3 - 3 - 7 = 9
c₁₄ = a₁₁ · b₁₄ + a₁₂ · b₂₄ + a₁₃ · b₃₄ + a₁₄ · b₄₄ = 2 · 1 + 1 · 3 + 3 · 1 + (-1) · 0 = 2 + 3 + 3 + 0 = 8
c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁ + a₂₃ · b₃₁ + a₂₄ · b₄₁ = 1 · 2 + 2 · (-4) + (-4) · 2 + 2 · 6 = 2 - 8 - 8 + 12 = -2
c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂ + a₂₃ · b₃₂ + a₂₄ · b₄₂ = 1 · 1 + 2 · (-2) + (-4) · 1 + 2 · 6 = 1 - 4 - 4 + 12 = 5

---

c₂₃ = a₂₁ · b₁₃ + a₂₂ · b₂₃ + a₂₃ · b₃₃ + a₂₄ · b₄₃ = 1 · 8 + 2 · 3 + (-4) · (-1) + 2 · 7 = 8 + 6 + 4 + 14 = 32
c₂₄ = a₂₁ · b₁₄ + a₂₂ · b₂₄ + a₂₃ · b₃₄ + a₂₄ · b₄₄ = 1 · 1 + 2 · 3 + (-4) · 1 + 2 · 0 = 1 + 6 - 4 + 0 = 3
c₃₁ = a₃₁ · b₁₁ + a₃₂ · b₂₁ + a₃₃ · b₃₁ + a₃₄ · b₄₁ = 1 · 2 + 0 · (-4) + 3 · 2 + 4 · 6 = 2 + 0 + 6 + 24 = 32
c₃₂ = a₃₁ · b₁₂ + a₃₂ · b₂₂ + a₃₃ · b₃₂ + a₃₄ · b₄₂ = 1 · 1 + 0 · (-2) + 3 · 1 + 4 · 6 = 1 + 0 + 3 + 24 = 28
c₃₃ = a₃₁ · b₁₃ + a₃₂ · b₂₃ + a₃₃ · b₃₃ + a₃₄ · b₄₃ = 1 · 8 + 0 · 3 + 3 · (-1) + 4 · 7 = 8 + 0 - 3 + 28 = 33
c₃₄ = a₃₁ · b₁₄ + a₃₂ · b₂₄ + a₃₃ · b₃₄ + a₃₄ · b₄₄ = 1 · 1 + 0 · 3 + 3 · 1 + 4 · 0 = 1 + 0 + 3 + 0 = 4
c₄₁ = a₄₁ · b₁₁ + a₄₂ · b₂₁ + a₄₃ · b₃₁ + a₄₄ · b₄₁ = 9 · 2 + 8 · (-4) + 1 · 2 + (-2) · 6 = 18 - 32 + 2 - 12 =-24
c₄₂ = a₄₁ · b₁₂ + a₄₂ · b₂₂ + a₄₃ · b₃₂ + a₄₄ · b₄₂ = 9 · 1 + 8 · (-2) + 1 · 1 + (-2) · 6 = 9 - 16 + 1 - 12 = -18
c₄₃ = a₄₁ · b₁₃ + a₄₂ · b₂₃ + a₄₃ · b₃₃ + a₄₄ · b₄₃ = 9 · 8 + 8 · 3 + 1 · (-1) + (-2) · 7 = 72 + 24 - 1 - 14 =81
c₄₄ = a₄₁ · b₁₄ + a₄₂ · b₂₄ + a₄₃ · b₃₄ + a₄₄ · b₄₄ = 9 · 1 + 8 · 3 + 1 · 1 + (-2) · 0 = 9 + 24 + 1 + 0 = 34

Ответ: произведение матриц равно .
Задание 2. Вычислить определитель:



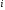Решение: пусть дана матрица порядка . Вычеркнем в ней -ю строку и 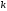-й столбец и сдвинем, не нарушая порядка, оставшиеся элементы. Определитель полученной матрицы 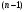-го порядка называется минором элемента 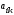и обозначается .

Найдем алгебраические дополнения элементов минора А по отдельности:

= +

---

+
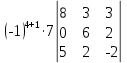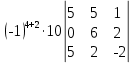
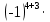
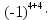+ 0 =-7 (-188)+10 (-60)+(-7) 96+0=1316+(-600)+(-672)=44
=8 6 (-2)+3 2 5+3 2 0-3 6 5-8 2 2-0 3 (-2)=-188
=5 6 (-2)+5 2 5+1 2 0-1 6 5-0 5 (-2)-5 2 2=-60+50+0-30-0-20=-60
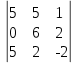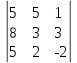=5

---

Смотрите также файлы

• 1. 1 Стадии технологического процесса.docx

• Диска.docx

• I. Химическая термодинамика (1й закон).rtf

• Курсовая работа по дисциплине Инвестиции студента заочной формы обучения направление подготовки 38. 03. 01 Экономика.docx

• Мектеп И.тпанлы ом малім.docx