Ответ:

4) От общего уравнения прямой перейти к каноническому, параметрическому и с угловым коэффициентом уравнениям прямой:

3x-2y+6=0.

Решение: общее уравнение прямой имеет вид: Ax+By+C=0


????̅ = (A, B)

????̅ = (A, B)-нормальный вектор прямой L

Пусть 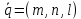-направляющий вектор прямой L и 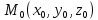- точка, лежащая на этой прямой
Вектор 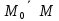, соединяющий точку с произвольной точкой

М (x, y, z) прямой L, параллельны вектору . Поэтому координаты вектора 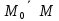= (x- и вектора 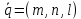пропорциональны, отсюда следует:

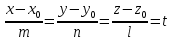(9)

Уравнения (9) называются каноническими уравнениями прямой в пространстве.

Найдем одно неизвестное, через другое:

3x= 2y-6

x=



M= (0, -3)

-2y= -6-3x

2y= 6-3x

y=


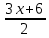
L

= (m, n, l)

=

M= (0, 2)

---

M = (x, y, z)


Из формулы (9) следует,что

- параметрическое уравнение (10)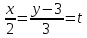









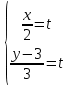
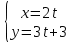
Уравнение прямой с угловым коэффициентом находим по формуле:

y= kx+b (9)

-2y=-3x-6

2y=3x+6

y=

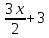
k=

Ответ: – каноническое уравнение, 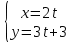- параметрическое уравнение, y= .

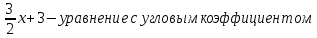5) Написать уравнение плоскости, проходящей через три заданные точки :

М₁(2,1,1), М₂=(1,2,1), М₃(1,1,2).

Решение:















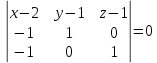
Ответ: - уравнение плоскости, проходящей через три заданные точки :

М₁(2,1,1), М₂=(1,2,1), М₃(1,1,2).

6) От общего уравнения прямой перейти к каноническому уравнению:



Решение: найдем направляющий вектор прямой L.

Из общих уравнений прямой

---

.

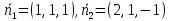
Найдем их векторное произведение:

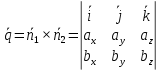(11)

,

То = (-2, 3,-1)

Найдем координаты любой точки,принадлежащей прямой L. Положим одну из координат равной нулю,например z = 0, тогда для координат x и y получим систему уравнений:



Откуда, x= -5, y= 8, то M (-5, 8, 0) 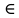L.

Запишем каноническое уравнение прямой по формуле(9)



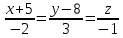
Ответ: 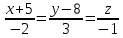– каноническое уравнение.

7) Найти угол между прямыми:

L₁:x+y-1=0, L₂: 2x-2y+1=0.






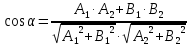
Ответ: угол между прямыми равен 90 .

8) Найдите расстояние от точки М до плоскости Р:

М(2,-3,-4), Р:x-y+2z-1=0

Представим ,что у нас есть некоторая плоскость Р:x-y+2z-1=0 и точка М(2,-3,-4), опустим из точки М перпендикуляр на плоскость Р и в месте их пересечения поставим точку 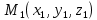. Расстояние от точки М до плоскости Р ,заданной уравнением Ах+Ву+Сz+D=0 ,можно найти по формуле:

c= 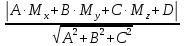(12)

c=

Ответ: расстояние от точки М до плоскости Р равно .

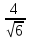9) Найти проекцию точки М на плоскость Р

М(2,1,-1), Р:2x-y-3z-1=0

Составим уравнение прямой перпендикулярно плоскости Р и проходящую через точку М ????̅=(2,-1,-3)

Запишем параметрические уравнения :





Найдем точку пересечения прямой и плоскости:



4t+4+t-1+9t-3-1=0

14t-1=0

14t=1

t=

---

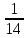
При t = найдем неизвестные:

x= 2 =

y=



Ответ: проекция точки М на плоскость Р ( , , ).

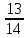10) . Составить уравнение эллипса, зная его большую полуось а и фокусы F1, F2:

a=6, F₁(-2,-1), F₂(6,-1).

Уравнение эллипса со смещенным центром имеет вид:

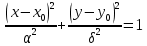(13)

Центр эллипса Q ( – это середина отрезка 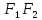, следовательно:

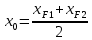; (14)

;

Соответственно центр эллипса Q(2,-1)

Расстояние между фокусами равно 2с,то есть

2с=





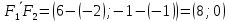
2c=8

c=4

Найдем полуось b:





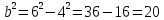
Тогда по формуле (13) уравнение эллипса имеет вид:



Ответ: уравнение эллипса .

---

Смотрите также файлы

• 1. 1 Стадии технологического процесса.docx

• Диска.docx

• I. Химическая термодинамика (1й закон).rtf

• Курсовая работа по дисциплине Инвестиции студента заочной формы обучения направление подготовки 38. 03. 01 Экономика.docx

• Мектеп И.тпанлы ом малім.docx