Файл: расчетнографическая работа на тему линейная алгебра.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3 (-2)+5
(-2)+5 3
3 5+1
5+1 2
2 8-1
8-1 3
3 5-5
5-5 2
2 3-8
3-8 5
5 (-2)=-30+75+16-15-30+80=96
(-2)=-30+75+16-15-30+80=96
Задание 3. Найти обратную матрицу для матрицы А:
А=
Квадратная матрица A называется вырожденной (особенной), если ее определитель равен нулю, и невырожденной (неособенной) в противном случае.
Если A - невырожденная матрица, то существует и притом единственная матрица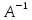 такая, что
такая, что
 , (2)
, (2)
где E - единичная матрица. Матрица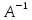 называется обратной к матрице A.
называется обратной к матрице A.
Справедливо равенство det А⸱Е. Отсюда следует, что если A - невырожденная матрица (det A 0), то
det А⸱Е. Отсюда следует, что если A - невырожденная матрица (det A 0), то
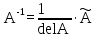 (3)
(3)
Найдем определитель матрицы:
Del A= =
=
Так как del A≠0, то система имеет единственное решение.
Найдем алгебраические дополнения элементов минора А
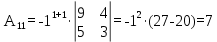
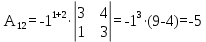

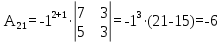
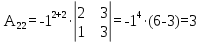
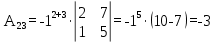

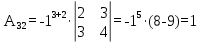
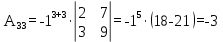
Запишем матрицу алгебраических дополнений:

Запишем союзную матрицу к матрице А:
 (4)
(4)
Найдем обратную матрицу по формуле (3):
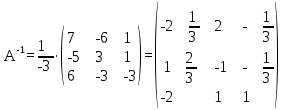
Ответ: обратная матрица для матрицы А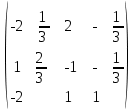
Задание 4. Решить системы уравнений:
а) Методом обратной матрицы: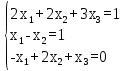
Запишем матрицу из системы уравнений:
 x=
x=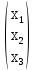 B=
B=
Найдем определитель матрицы А:
del A=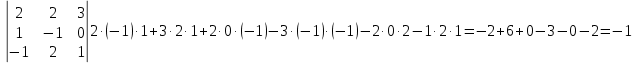
Так как detA≠0, то система имеет единственное решение.
Найдем алгебраические дополнения:

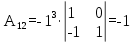
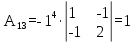
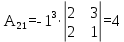

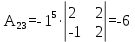

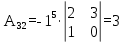

Запишем матрицу алгебраических дополнений:

Найдем союзную матрицу по формуле (4):
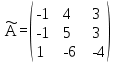
Найдем обратную матрицу по формуле (3):
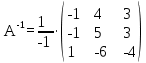 =
=
Найдем неизвестные Х:
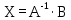 (5)
(5)
X= ⸱
⸱
=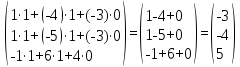
Ответ:
б) методом Крамера:
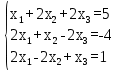
Найдем определитель системы:

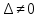 , значит эта система имеет единственное решение. Это решение момент быть найдено по формулам:
, значит эта система имеет единственное решение. Это решение момент быть найдено по формулам:
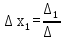 ,
, 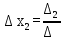 ,…,
,…, 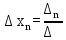 , (6)
, (6)
Где получается из
получается из 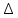 заменой
заменой 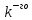 столбца на столбец свободных членов.
столбца на столбец свободных членов.
Найдем определители ,
,  :
:
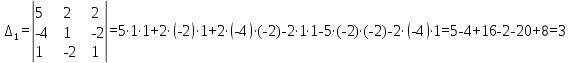
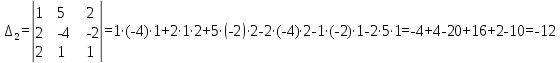

Найдем неизвестную по формулам (6)



Ответ: ,
,  ,
, 
в) Методом Гаусса:
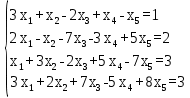
Запишем расширенную матрицу системы:
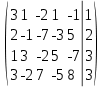
1 строчку поменяем местами с 3 строчкой
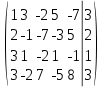
Умножим 1 строчку на -2 и прибавим к ней 2 строчку
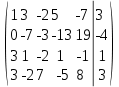
Умножим 1 страницу на -3 и прибавим к ней 3 строчку
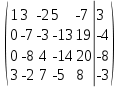
Умножим 1 страницу на -3 и прибавим к ней 4 строчку

Третью строчку умножим на -1 и сложим со второй строчкой
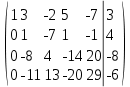
Вторую строчку -8 и сложим с третьей
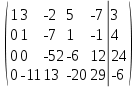
Вторую строчку -11 и сложим с четвертой
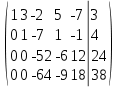
Третью строчку умножаем на и сложим с четвертой:
и сложим с четвертой:

Запишем системой:
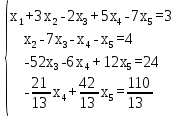
Найдем неизвестные:


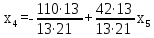



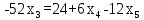
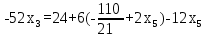

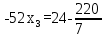

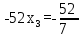
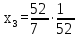
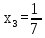
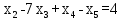
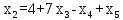
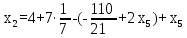
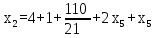

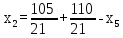


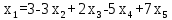
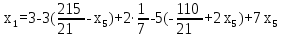

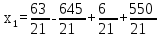
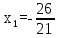
Ответ: Система имеет множество решений:
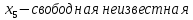
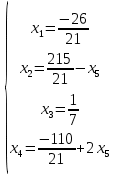
ЧАСТЬ 2
 = (1, 4),
= (1, 4), 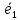 = (1, 3),
= (1, 3), 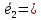 (-2, -3)
(-2, -3)
Решение: запишем векторное уравнение
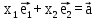 (7)
(7)
Запишем в виде матрицы
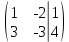
Решим методом Гаусса
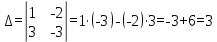
Так как , то система имеет единственное решение
, то система имеет единственное решение
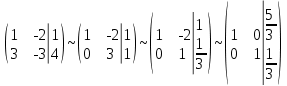
По формуле (7) получаем:

Если векторы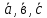 линейно – зависимые, то их смешанное произведение равно нулю.
линейно – зависимые, то их смешанное произведение равно нулю.
Проверим:
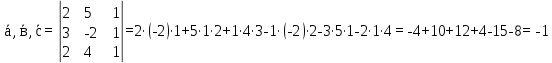
Ответ: векторы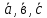 не линейно зависимые
не линейно зависимые
 = (1,3,2),
= (1,3,2),  = (1,2,2)
= (1,2,2)
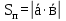 (8)
(8)
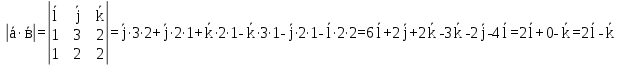
 (-2)+5
(-2)+5 3
3 5+1
5+1 2
2 8-1
8-1 3
3 5-5
5-5 2
2 3-8
3-8 5
5 (-2)=-30+75+16-15-30+80=96
(-2)=-30+75+16-15-30+80=96Задание 3. Найти обратную матрицу для матрицы А:
А=

Квадратная матрица A называется вырожденной (особенной), если ее определитель равен нулю, и невырожденной (неособенной) в противном случае.
Если A - невырожденная матрица, то существует и притом единственная матрица
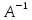 такая, что
такая, что  , (2)
, (2)где E - единичная матрица. Матрица
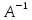 называется обратной к матрице A.
называется обратной к матрице A.Справедливо равенство
 det А⸱Е. Отсюда следует, что если A - невырожденная матрица (det A 0), то
det А⸱Е. Отсюда следует, что если A - невырожденная матрица (det A 0), то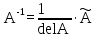 (3)
(3)Найдем определитель матрицы:
Del A=
 =
=
Так как del A≠0, то система имеет единственное решение.
Найдем алгебраические дополнения элементов минора А
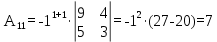
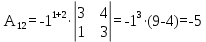

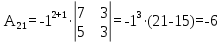
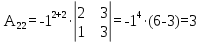
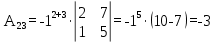

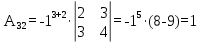
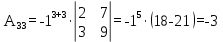
Запишем матрицу алгебраических дополнений:

Запишем союзную матрицу к матрице А:
 (4)
(4)Найдем обратную матрицу по формуле (3):
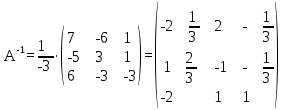
Ответ: обратная матрица для матрицы А
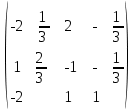
Задание 4. Решить системы уравнений:
а) Методом обратной матрицы:
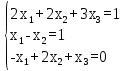
Запишем матрицу из системы уравнений:
 x=
x= B=
B=
Найдем определитель матрицы А:
del A=
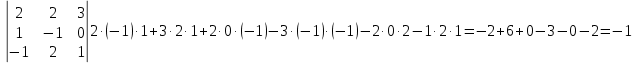
Так как detA≠0, то система имеет единственное решение.
Найдем алгебраические дополнения:

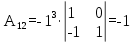
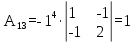
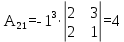

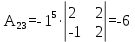

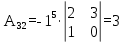

Запишем матрицу алгебраических дополнений:

Найдем союзную матрицу по формуле (4):
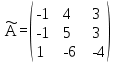
Найдем обратную матрицу по формуле (3):
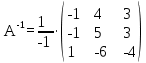 =
=
Найдем неизвестные Х:
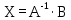 (5)
(5)X=
 ⸱
⸱
=
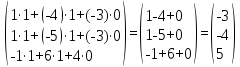
Ответ:

б) методом Крамера:
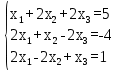
Найдем определитель системы:

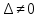 , значит эта система имеет единственное решение. Это решение момент быть найдено по формулам:
, значит эта система имеет единственное решение. Это решение момент быть найдено по формулам: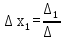 ,
, 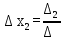 ,…,
,…, 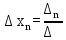 , (6)
, (6)Где
 получается из
получается из 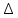 заменой
заменой 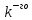 столбца на столбец свободных членов.
столбца на столбец свободных членов.Найдем определители
 ,
,  :
: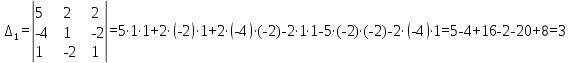
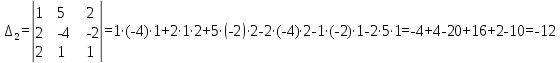

Найдем неизвестную по формулам (6)



Ответ:
 ,
,  ,
, 
в) Методом Гаусса:
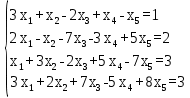
Запишем расширенную матрицу системы:
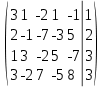
1 строчку поменяем местами с 3 строчкой
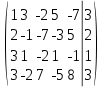
Умножим 1 строчку на -2 и прибавим к ней 2 строчку
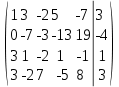
Умножим 1 страницу на -3 и прибавим к ней 3 строчку
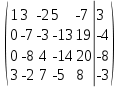
Умножим 1 страницу на -3 и прибавим к ней 4 строчку

Третью строчку умножим на -1 и сложим со второй строчкой
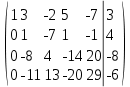
Вторую строчку -8 и сложим с третьей
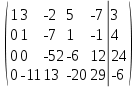
Вторую строчку -11 и сложим с четвертой
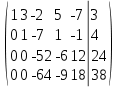
Третью строчку умножаем на
 и сложим с четвертой:
и сложим с четвертой:
Запишем системой:
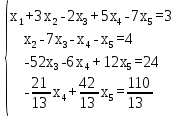
Найдем неизвестные:


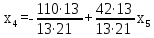



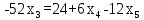
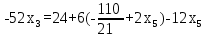

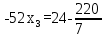

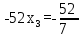
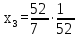
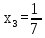
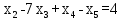
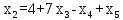
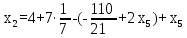
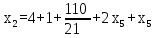

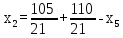


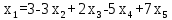
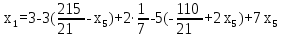

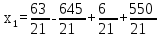
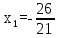
Ответ: Система имеет множество решений:
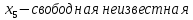
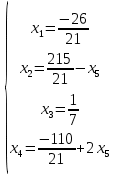
ЧАСТЬ 2
-
Написать разложение вектора по базису
по базису 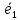 ,
, 
 = (1, 4),
= (1, 4), 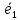 = (1, 3),
= (1, 3), 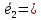 (-2, -3)
(-2, -3)Решение: запишем векторное уравнение
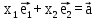 (7)
(7)Запишем в виде матрицы
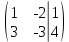
Решим методом Гаусса
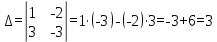
Так как
 , то система имеет единственное решение
, то система имеет единственное решение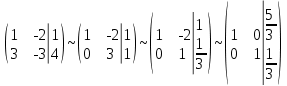
По формуле (7) получаем:

Если векторы
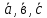 линейно – зависимые, то их смешанное произведение равно нулю.
линейно – зависимые, то их смешанное произведение равно нулю.Проверим:
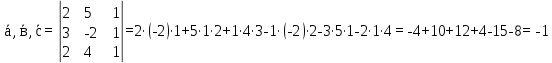
Ответ: векторы
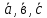 не линейно зависимые
не линейно зависимые-
Найти площадь параллелограмма, построенного на векторах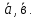
 = (1,3,2),
= (1,3,2),  = (1,2,2)
= (1,2,2)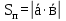 (8)
(8)