ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 35
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
л. Аналогично расчёту ОЛ и Т в момент Dкр рассчитывают траверзные ОЛ и Т. Угол между D и Dкр будет равен суммарному углу сноса с.
Второй случай: известен только суммарный угол сноса с. В этом случае на карте прокладываются две линии: ИК и ПУс и также решаются прямая и обратная задачи аналогично как и в первом случае, только при прямой задаче из конца вектора скорости судна по лагу Vл, откладывается вектор суммарного сноса с. Соединение начальной точки с концом этого вектора даёт линию пути при суммарном действии ветра и течения ПУс и вектор путевой скорости V.
При обратной задаче из начальной точки проложенного на карте пути ПУс, по которому должно следовать судно несмотря на совместное действие ветра и течения, откладывается вектор суммарного сноса с, из конца которого радиусом равным Vл делается засечка на линии ПУс. Отрезок от исходной точки до засечки на линии пути - это вектор путевой скорости V. Направление полученной линии переносится в начальную точку и представляет собой линию ИК.
Надпись на карте при совместном учете ветра и течения состоит из ГКК, ГК, КК, МК и угла суммарного сноса с с его знаком.
Навигационные методы определения пути судна.
В
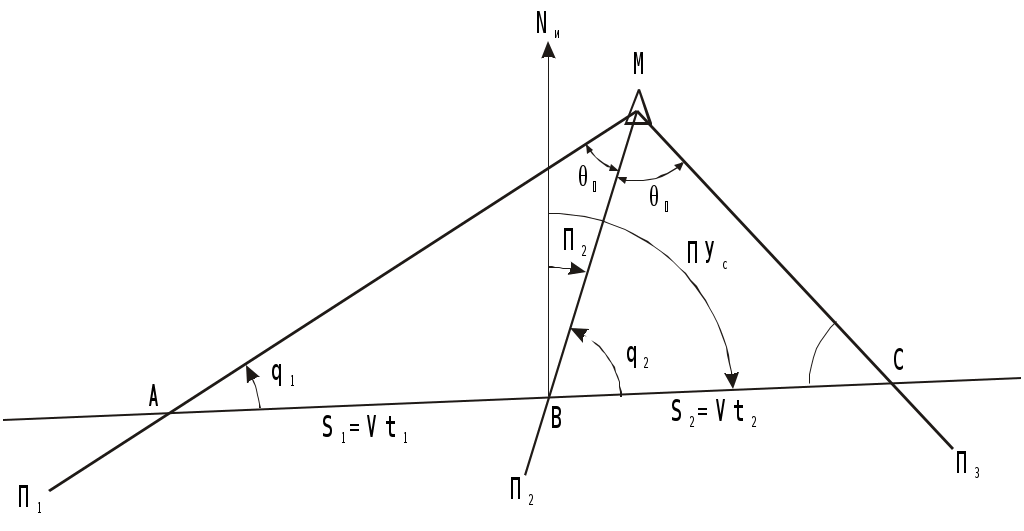 Рис. 4.29. Определение пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
Рис. 4.29. Определение пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
практике судовождения часто судоводитель не знает отдельно каждые из элементов сноса течением и дрейфа от ветра, но может получить путь и суммарный угол сноса самым простым и надёжным способом - по обсервациям (см.п.4.1.4). Именно знание пути и действительной скорости судна относительно Земли является главной задачей судоводителя для обеспечения безопасности судовождения. Если по каким-либо причинам нельзя использовать этот метод, то направление линии пути можно определить по любому неподвижному ориентиру, который даже может быть и не нанесён на карту. Для этого надо трижды измерить пеленга на этот ориентир и как можно точнее измерить промежутки времени между этими пеленгами. Судно при этом должно следовать постоянным курсом и скоростью. Итак, в фиксированные с точностью до секунды моменты времени измеряют три пеленга П
1, П2 и П3 любого неподвижного ориентира. Этот способ определения пути основан на том, что любая прямая, пересекающая три пеленга так, что её отрезки между пеленгами относятся как S1/ S2 = Vt1/ Vt2 = t1/ t2, будет параллельна линии пути. Для получения линии пути надо найти угол q2 (рис.4.29) и, сложив его с измеренным П2, получить ПУс:
ПУс = П2 + ( q2), (4.50)
q2 имеет знак “+”, если предмет расположен слева, и знак “” если справа.
Обозначим через t1 время плавания между первым и вторым пеленгами и через 1- угол между этими пеленгами; через t2 - обозначим время плавания между вторым и третьим пеленгами и через 2 - угол между вторым и третьим пеленгами.
Из АМВ угол q2 = q1 + 1 как внешний, отсюда q1 = q2 1.
Из ВМС угол С =180 (q2+2).
Из АМВ и ВМС найдём значения ВМ:
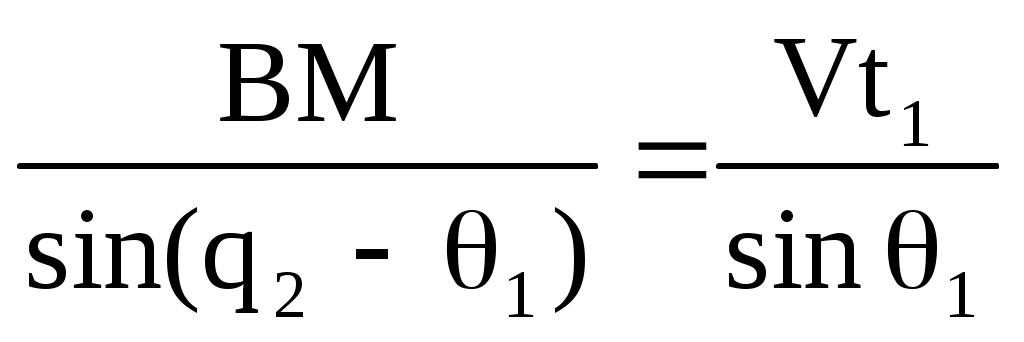 ,
, 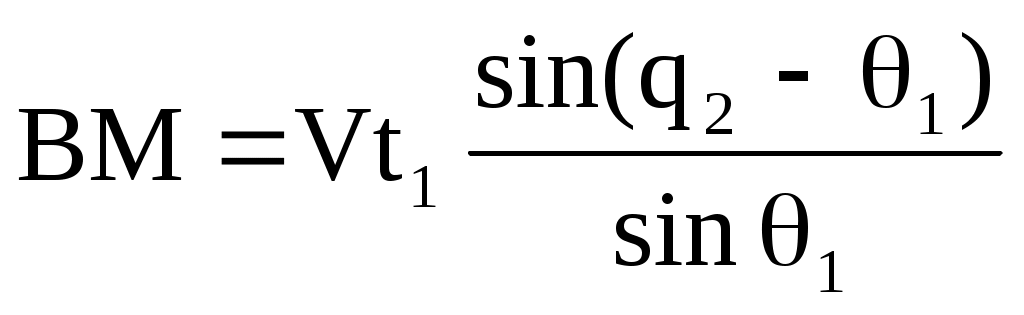 ,
,
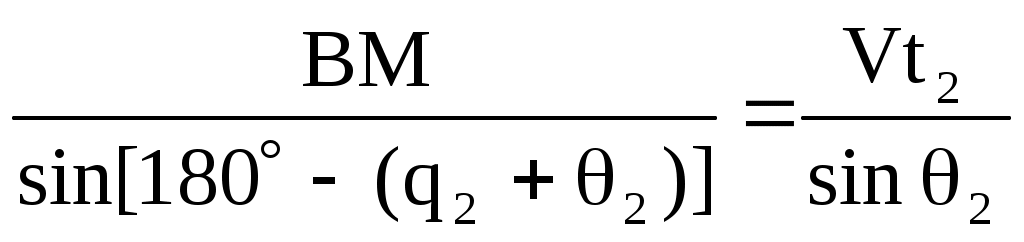 ,
, 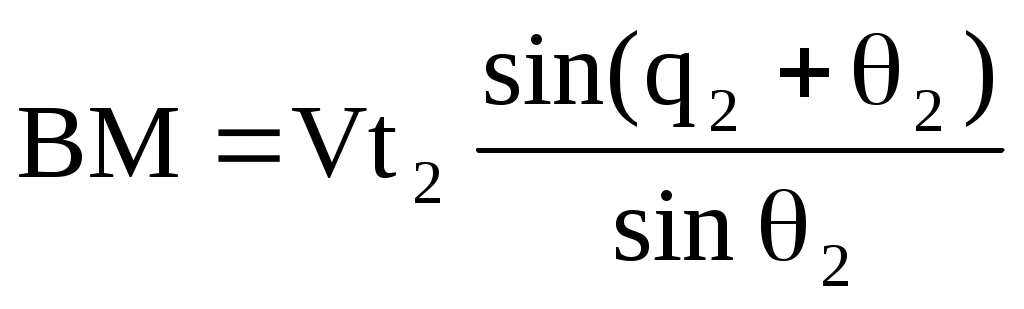 , т.к. sin(180)=sin.
, т.к. sin(180)=sin.
Следовательно
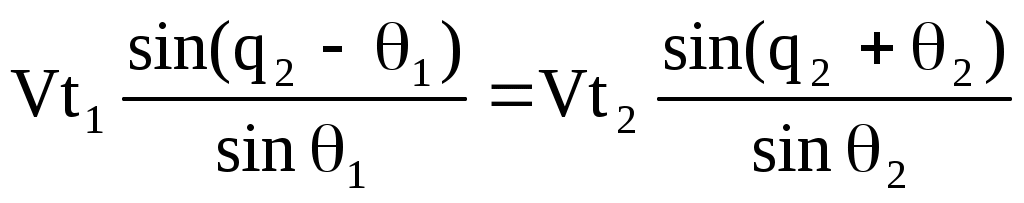
t1sinq21 sin2 = t2sinq2+2 sin1.
Используя формулы сложения и вычитания синусов
sin(a b) = sin a cos b cos a sin b,
получим:
t1 (sin q2 cos 1 cos q2 sin 1) sin 2 = t2 (sin q2 cos 2+ cosq2 sin2) sin1.
Разделим каждое слагаемое на sinq2 sin1 sin2:
t1 ctg1 t1 ctgq2 = t2 ctg2 + t2 ctgq2.
Откуда определим
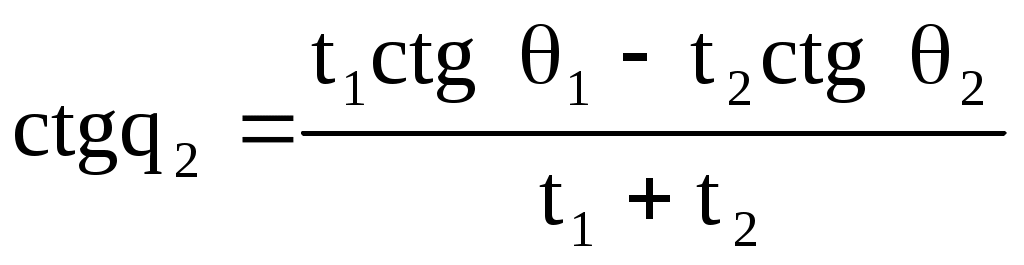 . (4.51)
. (4.51)
По формуле (4.50) рассчитаем путь судна.
Если пеленга взяты через равные промежутки времени, то формула (4.51) упростится
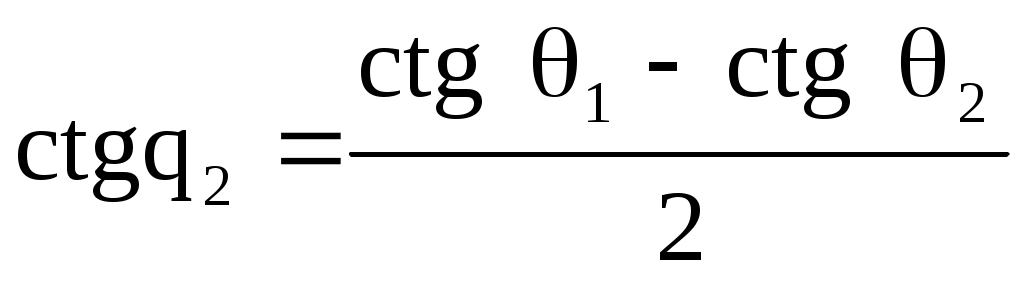 . (4.52)
. (4.52)
Эта задача имеет и графическое решение (рис.4.30).
И
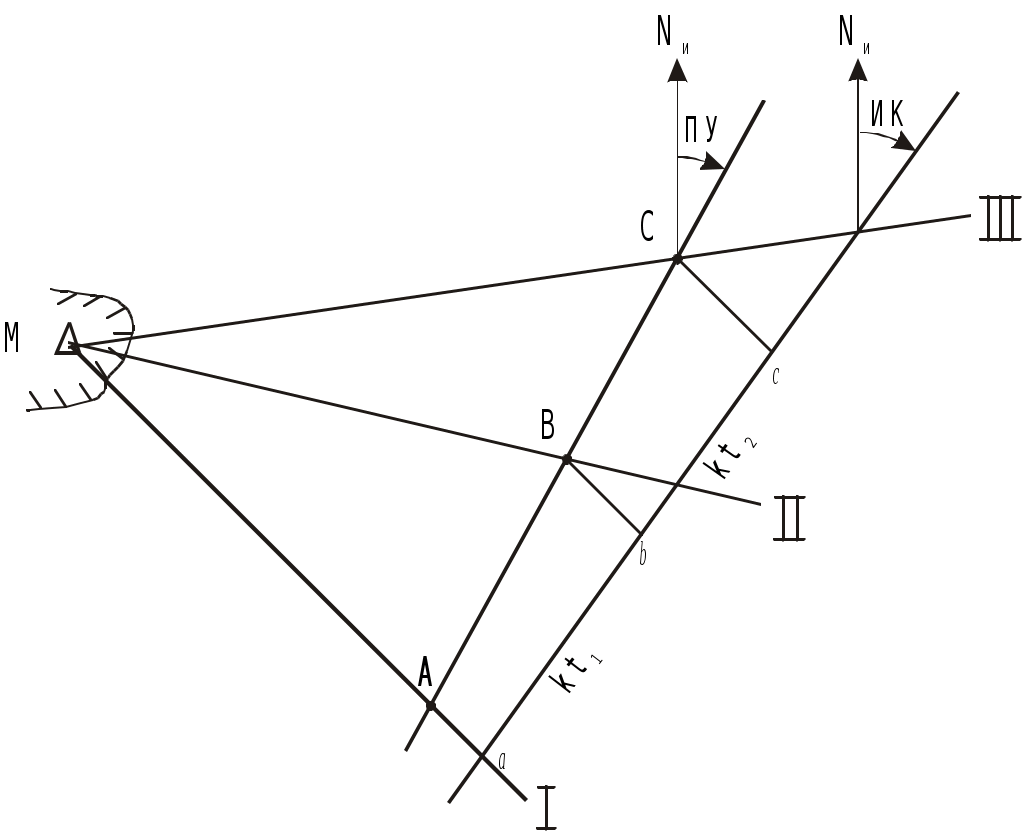 Рис. 4.30. Графическое решение задачи определения пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
Рис. 4.30. Графическое решение задачи определения пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
з произвольной точки на свободном месте карты прокладывают 3 измеренных пеленга. Из произвольной точки a на первом пеленге проводят линию ИК (можно и произвольную линию), на которой откладывают отрезки пропорциональные времени плавания: kt1из точки а и kt2 из точки в (k -произвольный коэффициент). Из полученных точек в и с проводят линии параллельные первому пеленгу до пересечения их со вторым пеленгом в точке В и третьим - в точке С. Прямая АВС будет параллельна линии пути. Этот приём основан на свойстве параллельных прямых, пересекающих пучок прямых:
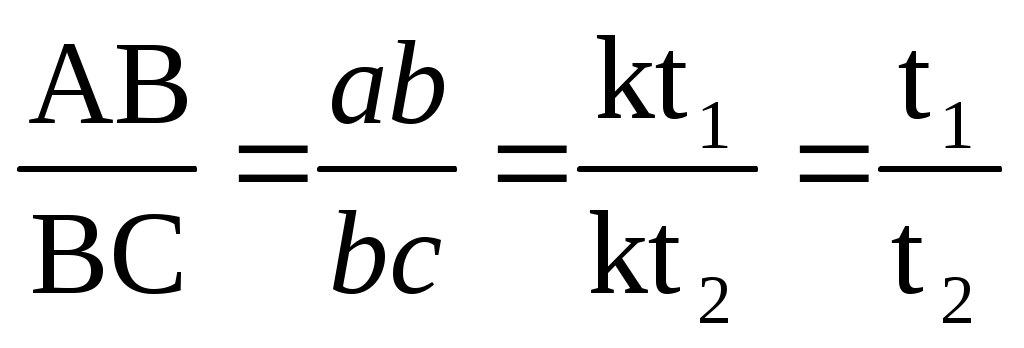
Е

Рис. 4.31. Определение пути по трем пеленгам неподвижного ориентира, взятым через равные промежутки времени
сли пеленга брать через равные промежутки времени, то графическое решение ещё упростится. Из произвольной точки n на втором пеленге (рис.4.31) проводят линии параллельные первому (nС) и третьему (nA) пеленгам. Линия AС будет параллельна направлению линии пути, т.к. на основании свойства диагоналей параллелограмма АВ = ВС, т.е за равные промежутки времени судно проходит равные расстояния.
Графическое решение может быть выполнено и с помощью линейки, на которой отложены отрезки пропорциональные плаваниям S1 = kt1 и S2 = kt2(точки а, в и с на линейке) (рис.4.32). Линейку надо расположить так, чтобы точки а, b и с лежали соответственно на первом, втором и третьем пеленгах. Прямая, проведённая через эти точки будет параллельна линии пути.
Для повышения точности все графические построения надо делать в возможно более крупном масштабе.
О
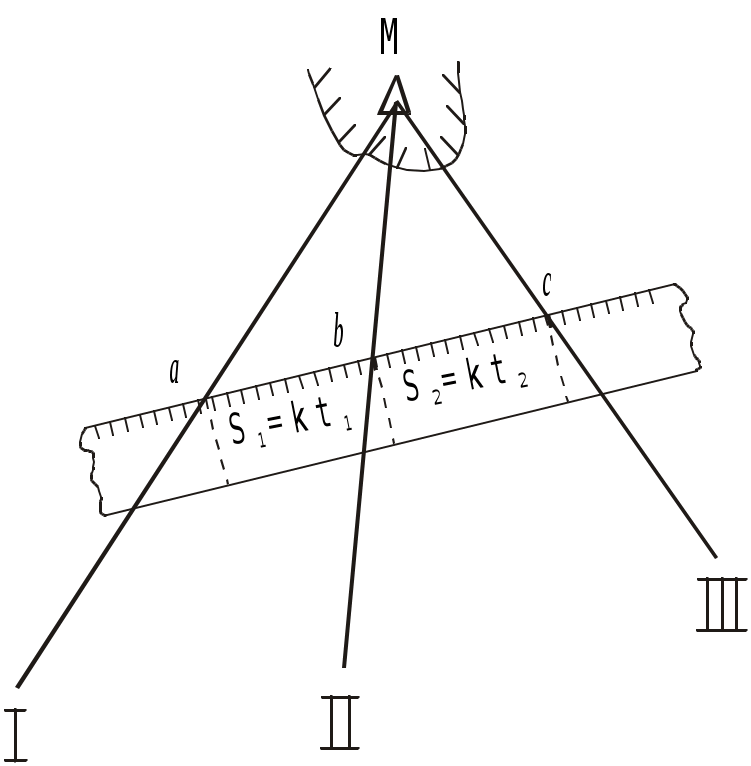
Рис. 4.32. Определение пути с помощью линейки по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
пределение суммарного сноса по пеленгам неподвижного ориентира и времени производится с достаточно высокой точностью, т.к. погрешностями в отсчётах времени t1 и t2 при использовании секундомера можно пренебречь, а в формулу расчёта q2 входят только углы 1 и 2
, представляющие собой разности пеленгов, т.е. систематические ошибки в пеленгах также не скажутся на точности q2.
При определении суммарного пути судна по формуле (4.50), если пеленг будет содержать погрешность в поправке компаса, то полученное направление пути также будет содержать эту погрешность. А на величине суммарного сноса эта погрешность не скажется, т.к. угол с получается, как разность ПУс и ИК, а ПУс и ИК будут ошибочны на одну и ту же величину погрешности в поправке компаса.
На величине q2 скажутся только случайные погрешности пеленгования, т.к. углы 1 и 2 рассчитываются по значениям пеленгов.
При достаточно больших углах 1, 2 и mп = 0,3 случайные погрешности в определении q2 находятся в пределах 1.
Пример. С судна, следующего ИК = 34 через промежутки времени t1 = 24 мин 03с и t2 = 25 мин 59c измерены пеленга на буровую вышку не нанесённую на карту: ГКП1 = 314, ГКП2 = 282 и ГКП3 = 256 (ГК = 0). Определить путь судна ПУс и суммарный угол сноса с.
Если при выполнении этого способа пеленга берутся до неподвижного ориентира и прокладываются на карте непосредственно от ориентира, нанесенного на карту, то получают фактическую линию суммарного пути, по которому следует судно,, ПУс, и суммарный угол сноса с = ПУс ИК.
Если же пеленга прокладываются от точки, изображающей ориентир, нанесенный на любом свободном месте карты, то получают линию параллельную линии суммарного пути ПУс и суммарный угол сноса с = ПУс ИК.
Если же пеленга берутся до свободноплавающего ориентира, то определяется только линия пути при дрейфе ПУ и, соответственно, угол дрейфа = ПУ ИК. Влияние течения практически исключается.
Точность графического счисления
Возможные погрешности в элементах счисления, углах дрейфа и сноса, поправках компаса и лага, а также в графических построениях на карте, которые накапливаются, приводят к тому, что при ведении прокладки действительное место судна не совпадает с нанесённым на карту счислимым местом. Судоводитель должен уметь оценить точность графического счисления. Погрешности счисления разделим на две группы: погрешность в определении пути судна и погрешность в пройденном расстоянии. Погрешностями графических построений пренебрегаем ввиду их малости.
С
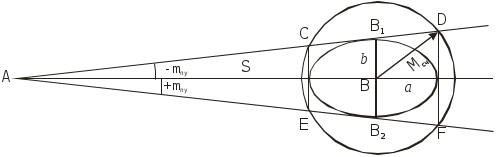 Рис. 4.33. Погрешность счисления за время плавания по счислению
Рис. 4.33. Погрешность счисления за время плавания по счислению
Второй случай: известен только суммарный угол сноса с. В этом случае на карте прокладываются две линии: ИК и ПУс и также решаются прямая и обратная задачи аналогично как и в первом случае, только при прямой задаче из конца вектора скорости судна по лагу Vл, откладывается вектор суммарного сноса с. Соединение начальной точки с концом этого вектора даёт линию пути при суммарном действии ветра и течения ПУс и вектор путевой скорости V.
При обратной задаче из начальной точки проложенного на карте пути ПУс, по которому должно следовать судно несмотря на совместное действие ветра и течения, откладывается вектор суммарного сноса с, из конца которого радиусом равным Vл делается засечка на линии ПУс. Отрезок от исходной точки до засечки на линии пути - это вектор путевой скорости V. Направление полученной линии переносится в начальную точку и представляет собой линию ИК.
Надпись на карте при совместном учете ветра и течения состоит из ГКК, ГК, КК, МК и угла суммарного сноса с с его знаком.
Навигационные методы определения пути судна.
В
 Рис. 4.29. Определение пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
Рис. 4.29. Определение пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгамипрактике судовождения часто судоводитель не знает отдельно каждые из элементов сноса течением и дрейфа от ветра, но может получить путь и суммарный угол сноса самым простым и надёжным способом - по обсервациям (см.п.4.1.4). Именно знание пути и действительной скорости судна относительно Земли является главной задачей судоводителя для обеспечения безопасности судовождения. Если по каким-либо причинам нельзя использовать этот метод, то направление линии пути можно определить по любому неподвижному ориентиру, который даже может быть и не нанесён на карту. Для этого надо трижды измерить пеленга на этот ориентир и как можно точнее измерить промежутки времени между этими пеленгами. Судно при этом должно следовать постоянным курсом и скоростью. Итак, в фиксированные с точностью до секунды моменты времени измеряют три пеленга П
1, П2 и П3 любого неподвижного ориентира. Этот способ определения пути основан на том, что любая прямая, пересекающая три пеленга так, что её отрезки между пеленгами относятся как S1/ S2 = Vt1/ Vt2 = t1/ t2, будет параллельна линии пути. Для получения линии пути надо найти угол q2 (рис.4.29) и, сложив его с измеренным П2, получить ПУс:
ПУс = П2 + ( q2), (4.50)
q2 имеет знак “+”, если предмет расположен слева, и знак “” если справа.
Обозначим через t1 время плавания между первым и вторым пеленгами и через 1- угол между этими пеленгами; через t2 - обозначим время плавания между вторым и третьим пеленгами и через 2 - угол между вторым и третьим пеленгами.
Из АМВ угол q2 = q1 + 1 как внешний, отсюда q1 = q2 1.
Из ВМС угол С =180 (q2+2).
Из АМВ и ВМС найдём значения ВМ:
Следовательно
t1sinq21 sin2 = t2sinq2+2 sin1.
Используя формулы сложения и вычитания синусов
sin(a b) = sin a cos b cos a sin b,
получим:
t1 (sin q2 cos 1 cos q2 sin 1) sin 2 = t2 (sin q2 cos 2+ cosq2 sin2) sin1.
Разделим каждое слагаемое на sinq2 sin1 sin2:
t1 ctg1 t1 ctgq2 = t2 ctg2 + t2 ctgq2.
Откуда определим
По формуле (4.50) рассчитаем путь судна.
Если пеленга взяты через равные промежутки времени, то формула (4.51) упростится
Эта задача имеет и графическое решение (рис.4.30).
И
 Рис. 4.30. Графическое решение задачи определения пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
Рис. 4.30. Графическое решение задачи определения пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгамиз произвольной точки на свободном месте карты прокладывают 3 измеренных пеленга. Из произвольной точки a на первом пеленге проводят линию ИК (можно и произвольную линию), на которой откладывают отрезки пропорциональные времени плавания: kt1из точки а и kt2 из точки в (k -произвольный коэффициент). Из полученных точек в и с проводят линии параллельные первому пеленгу до пересечения их со вторым пеленгом в точке В и третьим - в точке С. Прямая АВС будет параллельна линии пути. Этот приём основан на свойстве параллельных прямых, пересекающих пучок прямых:
Е

Рис. 4.31. Определение пути по трем пеленгам неподвижного ориентира, взятым через равные промежутки времени
сли пеленга брать через равные промежутки времени, то графическое решение ещё упростится. Из произвольной точки n на втором пеленге (рис.4.31) проводят линии параллельные первому (nС) и третьему (nA) пеленгам. Линия AС будет параллельна направлению линии пути, т.к. на основании свойства диагоналей параллелограмма АВ = ВС, т.е за равные промежутки времени судно проходит равные расстояния.
Графическое решение может быть выполнено и с помощью линейки, на которой отложены отрезки пропорциональные плаваниям S1 = kt1 и S2 = kt2(точки а, в и с на линейке) (рис.4.32). Линейку надо расположить так, чтобы точки а, b и с лежали соответственно на первом, втором и третьем пеленгах. Прямая, проведённая через эти точки будет параллельна линии пути.
Для повышения точности все графические построения надо делать в возможно более крупном масштабе.
О

Рис. 4.32. Определение пути с помощью линейки по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
пределение суммарного сноса по пеленгам неподвижного ориентира и времени производится с достаточно высокой точностью, т.к. погрешностями в отсчётах времени t1 и t2 при использовании секундомера можно пренебречь, а в формулу расчёта q2 входят только углы 1 и 2
, представляющие собой разности пеленгов, т.е. систематические ошибки в пеленгах также не скажутся на точности q2.
При определении суммарного пути судна по формуле (4.50), если пеленг будет содержать погрешность в поправке компаса, то полученное направление пути также будет содержать эту погрешность. А на величине суммарного сноса эта погрешность не скажется, т.к. угол с получается, как разность ПУс и ИК, а ПУс и ИК будут ошибочны на одну и ту же величину погрешности в поправке компаса.
На величине q2 скажутся только случайные погрешности пеленгования, т.к. углы 1 и 2 рассчитываются по значениям пеленгов.
При достаточно больших углах 1, 2 и mп = 0,3 случайные погрешности в определении q2 находятся в пределах 1.
Пример. С судна, следующего ИК = 34 через промежутки времени t1 = 24 мин 03с и t2 = 25 мин 59c измерены пеленга на буровую вышку не нанесённую на карту: ГКП1 = 314, ГКП2 = 282 и ГКП3 = 256 (ГК = 0). Определить путь судна ПУс и суммарный угол сноса с.
-
От произвольной точки М (рис4.30) отложили ОИП1 = 134, ОИП2 = 102 и ОИП3 = 76. -
Переведя t1 и t2 в секунды и приняв коэффициент k = 0,01, получили k t1 = 14,43 и k t2 = 15,59, отложили эти величины в сантиметрах или милях по линии ИК от первого пеленга (точка а). Из полученных точек в и с провели линии параллельные ОИП1 и соединили точки В и С линией пути ПУс = 28. Суммарный угол сноса с = 28 34 = 6.
Если при выполнении этого способа пеленга берутся до неподвижного ориентира и прокладываются на карте непосредственно от ориентира, нанесенного на карту, то получают фактическую линию суммарного пути, по которому следует судно,, ПУс, и суммарный угол сноса с = ПУс ИК.
Если же пеленга прокладываются от точки, изображающей ориентир, нанесенный на любом свободном месте карты, то получают линию параллельную линии суммарного пути ПУс и суммарный угол сноса с = ПУс ИК.
Если же пеленга берутся до свободноплавающего ориентира, то определяется только линия пути при дрейфе ПУ и, соответственно, угол дрейфа = ПУ ИК. Влияние течения практически исключается.
Точность графического счисления
Возможные погрешности в элементах счисления, углах дрейфа и сноса, поправках компаса и лага, а также в графических построениях на карте, которые накапливаются, приводят к тому, что при ведении прокладки действительное место судна не совпадает с нанесённым на карту счислимым местом. Судоводитель должен уметь оценить точность графического счисления. Погрешности счисления разделим на две группы: погрешность в определении пути судна и погрешность в пройденном расстоянии. Погрешностями графических построений пренебрегаем ввиду их малости.
С
 Рис. 4.33. Погрешность счисления за время плавания по счислению
Рис. 4.33. Погрешность счисления за время плавания по счислению

