Файл: Контрольная работа по разделу Множества. Математические утверждения и их структура Множество. Элемент множества. Способы задания множества. Числовые множества.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 36
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, если в классе есть девочки-отличницы.
А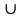 В
В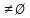 , если в классе есть хотя бы одна девочка или хотя бы один отличник.
, если в классе есть хотя бы одна девочка или хотя бы один отличник.
А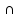 В = В, если все отличники являются девочками.
В = В, если все отличники являются девочками.
А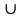 В = В, если все девочки в классе — отличницы.
В = В, если все девочки в классе — отличницы.
P={1,2,3,6,9,18}
Q={1,2,3,4,6,8,12,24}
P∩Q={1,2,3,6}. Характеристическое свойство — множество натуральных делителей числа 6.
а) 21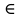 К∩М;
К∩М;
б) 32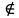 К ∩ М;
К ∩ М;
в) 32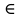 К U М;
К U М;
г) 7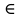 К ∩М;
К ∩М;
д) 7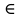 КUМ;
КUМ;
е) 135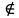 К UM?
К UM?
Решение: К∩М= {x| x- нечётные числа от 11 до 99}
К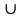 М=[10;99]
М=[10;99]
Верно ли, что:
а) 21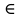 К∩М - истина
К∩М - истина
б) 32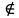 К ∩ М - истина
К ∩ М - истина
в) 32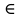 К U М - истина
К U М - истина
г) 7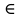 К ∩ - ложь
К ∩ - ложь
д) 7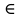 КUМ - ложь
КUМ - ложь
е) 135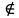 К U M - истина
К U M - истина

S∩T = квадраты
SUT=правильные n-угольники и прямоугольники
К S∩T относится квадрат F4
К SUT относятся фигуры F1, F4 – прямоугольник и квадрат
Дополнение к множеству. Разность множеств. Универсальное множество.
Практические задания для самостоятельной работы
а) В = {с, d, е, f, k, l};
б) В = {a, c, e};
в) B = {c, a, d. e, b};
r) B = {k, t, m};
д) В = {a, b, c, d, e, f, k};
e) В = .
.
Решение: a) A\B={a,b}
б) A\B={b,d}
в) A\B=
г) A\B={а, b, с, d, е}
д) A\B=
е) A\B={а, b, с, d, е}
Решение: А \ В={2,3,4} и В \ А={11,12,13,14,15,16,17,18,19,20}
Решение: Все элементы множества Р\Q должны быть нечётными двузначными числами.
Р\Q содержит числа 21, 17 — истина, так как 21 и 17 являются нечётными двузначными числами.

Дано множество Х = {а, b, с, d, е, f}. Запишите два подмножества множества
Xи дополнения этих подмножеств до множества X.
Решение: множество А={a,b,c} и множество В={d,e,f} являются подмножествами множества Х.
подмножество А={a,b,c} –дополнением является подмножество А’=В={d,e,f}
подмножество В={d,e,f} – дополнением является подмножество В’=А={a,b,c}
а) Р - множество остроугольных треугольников;
б) Р - множество равносторонних треугольников.
Решение: а) Дополнение Р’ к множеству Р имеет следующее характеристическое свойство элементов — это множество прямоугольных и тупоугольных треугольников.
б) Дополнение Р’ к множеству Р имеет следующее характеристическое свойство элементов — это множество треугольников с неравными сторонами.
Решение: а) Дополнение к множеству четных натуральных чисел до множества N это множество нечётных натуральных чисел.
б) Дополнение к множеству отрицательных чисел до множества Z это множество неотрицательных целых чисел (N+0)или N0
в) Дополнение к множеству целых чисел до множества Q это множество дробных чисел.
Кортеж
Практические задания для самостоятельной работы
Решение: В слове колокол 7 букв, Различных букв в этом слове 3: к,о,л.
Решение: Они образуют множество{к,о,л}. Кортеж букв <к,о,л,о,к,о,л>
Решение: в записи числа 56 576 - 5 цифр. Различных цифр 3: 5,6,7
Решение: Задача. Запишите множество цифр, с помощью которых написано число 56 576. Запишите кортеж цифр, с помощью которых написано число 56 576.
Решение: Множество букв, входящих в слово «шар»{ш,а,р}
Все возможные кортежи: <ш>, <а>, <р>, <ш,а>, <а,р>, <ш,р>, <а,ш>, <р,а>, <р,ш>, <ш,а,р>, <а,р,ш>, <р,а,ш>, <ш,р,а>,<а,ш,р>, <р,ш,а>.
а) <2, 1, 0, 5, 1, 9, 7, 0> и <2, 1, 0, 5, 1, 9, 7, 0>;
б) <ч, ю, д, о, в, и, щ, е> и < ч, у, д, о, в, и, щ, е>;
в) <п,а,р,а,л,л,е,л,о,г,р,а,м,м> и < п,а,р,а,л,л,е,л,о,г,р,а,м>.
Решение: а) <2, 1, 0, 5, 1, 9, 7, 0> и <2, 1, 0, 5, 1, 9, 7, 0>.
Данные кортежи являются равными, так как кортежи имеют одинаковое число компонент, т.е. одинаковую длину и каждая компонента первого кортежа равна компоненте второго кортежа с тем же номером.
б) <ч, ю, д, о, в, и, щ, е> и < ч, у, д, о, в, и, щ, е>;
Оба кортежа имеют одинаковую длину, но компонента первого кортежа под порядковым номером 2 является буква ю, а компонента второго кортежа с тем же порядковым номером буква у. ю≠у, следовательно, кортежи не равны.
в) <п,а,р,а,л,л,е,л,о,г,р,а,м,м> и < п,а,р,а,л,л,е,л,о,г,р,а,м>. Количество компонент первого кортежа – его длина равна 14, а количество компонент второго кортежа равна 13. Кортежи имеют разную длину, т.е. не равны.
Декартово произведение множеств
Практические задания для самостоятельной работы
Решение: А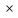 В = {(4,3), (4,7), (5,3), (5,7), (6,3), (6,7)}.
В = {(4,3), (4,7), (5,3), (5,7), (6,3), (6,7)}.
Решение: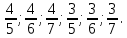
а) X = {а, b, с}, Y = {к, l};
б) X = {a, b,c}, Y = {d};
в) X = {а, b, с}, Y=X;
г) X = {а, b, с}, Y = .
.
Решение: а) X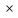 Y={(a, k), (a,l), (b, k), (b,l), (c,k),(c,l)}
Y={(a, k), (a,l), (b, k), (b,l), (c,k),(c,l)}
б) X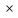
Y={(a, d), (b,d), (c, d)}
в) Y=X = {а, b, с} X Y={(a, a), (a,b), (a, c), (b,a), (b,b),(b,c), (c,a), (c,b), (c,c)}
Y={(a, a), (a,b), (a, c), (b,a), (b,b),(b,c), (c,a), (c,b), (c,c)}
г) X = {а, b, с}, Y = . Следовательно, X
. Следовательно, X Y=
Y=
Решение: Так как в декартовом произведении первая компонента пары принадлежит первому множеству, а вторая компонента пары принадлежит второму множеству, то А={2,3} B={3,5,6}
а) X = {-1, 0, 1, 2}, Y = {2, 3, 4};
б) X = {-1, 0, 1, 2}, Y = [2; 4];
в) X = [1; 2], Y={2, 3, 4};
г) X = [1; 7], Y = [2; 6];
д) X = [-3; 2], Y = [0; 5[;
е) Х = R, Y = [-2; 2];
ж) X = ]-3; 2[, Y = R;
з) Х = {2}, Y = R;
и) Х = R, Y={-3}.
Решение:
а) X = {-1, 0, 1, 2}, Y = {2, 3, 4}; X Y={(-1, 2), (-1,3), (-1,4), (0,2), (0,3), (0,4), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4)}
Y={(-1, 2), (-1,3), (-1,4), (0,2), (0,3), (0,4), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4)}
б) X = {-1, 0, 1, 2}, Y = [2; 4];
В данном примере множество Х- конечное, а множество Y – бесконечное множество действительных чисел от 2 (включая 2) до 4 (включая 4), поэтому перечислить все пары декартова произведения не представляется возможным, а результатом изображения будет четыре отрезка. Перечислим координаты концов отрезков :
(-1, 2) и (-1,4)
(0,2) и (0,4)
(1,2) и (1,4),
(2,2) и (2,4)
в) X = [1; 2], Y={2, 3, 4};
В данном примере множество Y- конечное, а множество Х – бесконечное множество действительных чисел от 1 (включая 1) до 2 (включая 2), поэтому перечислить все пары декартова произведения не представляется возможным, а результатом изображения будет четыре отрезка. Перечислим координаты концов отрезков
X Y={(1, 2), (1, 3),(1,4), (2,2), (2,3),(2,4)}
Y={(1, 2), (1, 3),(1,4), (2,2), (2,3),(2,4)}
(1,2) и (2,2)
(1,3) и (2,3)
(1,4) и (2,4)
г) X = [1; 7], Y = [2; 6];
В данном примере множество Х и множество Y – это бесконечные множества действительных чисел. Результатом изображения декартова произведения будет четырехугольник. Перечислим координаты его вершин :
А
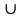 В
В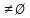 , если в классе есть хотя бы одна девочка или хотя бы один отличник.
, если в классе есть хотя бы одна девочка или хотя бы один отличник.А
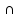 В = В, если все отличники являются девочками.
В = В, если все отличники являются девочками.А
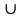 В = В, если все девочки в классе — отличницы.
В = В, если все девочки в классе — отличницы.-
Р - множество натуральных делителей числа 18, Q- множество натуральных делителей числа 24. Укажите характеристическое свойство элементов пересечения множеств Р и Quперечислите его элементы.
P={1,2,3,6,9,18}
Q={1,2,3,4,6,8,12,24}
P∩Q={1,2,3,6}. Характеристическое свойство — множество натуральных делителей числа 6.
-
Найдите пересечение и объединение множеств К и М, если К -множество двузначных чисел, М - множество нечетных чисел. Верно ли, что:
а) 21
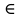 К∩М;
К∩М;б) 32
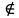 К ∩ М;
К ∩ М;в) 32
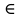 К U М;
К U М;г) 7
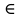 К ∩М;
К ∩М;д) 7
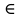 КUМ;
КUМ;е) 135
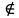 К UM?
К UM?Решение: К∩М= {x| x- нечётные числа от 11 до 99}
К
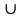 М=[10;99]
М=[10;99]Верно ли, что:
а) 21
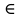 К∩М - истина
К∩М - истинаб) 32
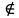 К ∩ М - истина
К ∩ М - истинав) 32
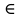 К U М - истина
К U М - истинаг) 7
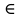 К ∩ - ложь
К ∩ - ложьд) 7
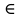 КUМ - ложь
КUМ - ложье) 135
 К U M - истина
К U M - истина
-
S - множество правильных многоугольников, Т -множество прямоугольников. Из каких фигур состоит пересечение и объединение множеств S н T? Какие из фигур, изображенных на рисунке 19, принадлежат пересечению множеств Sи Т, акакие - их объединению?

S∩T = квадраты
SUT=правильные n-угольники и прямоугольники
К S∩T относится квадрат F4
К SUT относятся фигуры F1, F4 – прямоугольник и квадрат
Дополнение к множеству. Разность множеств. Универсальное множество.
Практические задания для самостоятельной работы
-
Найдите разность множества А = {а, b, с, d, е} и множества В, если:
а) В = {с, d, е, f, k, l};
б) В = {a, c, e};
в) B = {c, a, d. e, b};
r) B = {k, t, m};
д) В = {a, b, c, d, e, f, k};
e) В =
 .
.Решение: a) A\B={a,b}
б) A\B={b,d}
в) A\B=

г) A\B={а, b, с, d, е}
д) A\B=

е) A\B={а, b, с, d, е}
-
Множество А состоит из натуральных чисел от 2 до 10, множество В - из натуральных чисел от 5 до 20. Перечислите элементы множеств А \ В и В \ А.
Решение: А \ В={2,3,4} и В \ А={11,12,13,14,15,16,17,18,19,20}
-
Р - множество двузначных чисел, Q- множество четных натуральных чисел. Изобразите данные множества при помощи кругов Эйлера, отметьте штриховкой разность множеств Р и Q и укажите характеристическое свойство элементов, принадлежащих этой разности. Верно ли, что Р \ Q содержит числа 21; 17?
Решение: Все элементы множества Р\Q должны быть нечётными двузначными числами.
Р\Q содержит числа 21, 17 — истина, так как 21 и 17 являются нечётными двузначными числами.

Дано множество Х = {а, b, с, d, е, f}. Запишите два подмножества множества
Xи дополнения этих подмножеств до множества X.
Решение: множество А={a,b,c} и множество В={d,e,f} являются подмножествами множества Х.
подмножество А={a,b,c} –дополнением является подмножество А’=В={d,e,f}
подмножество В={d,e,f} – дополнением является подмножество В’=А={a,b,c}
-
Сформулируйте характеристическое свойство элементов дополнения подмножества Р до множества треугольников, если:
а) Р - множество остроугольных треугольников;
б) Р - множество равносторонних треугольников.
Решение: а) Дополнение Р’ к множеству Р имеет следующее характеристическое свойство элементов — это множество прямоугольных и тупоугольных треугольников.
б) Дополнение Р’ к множеству Р имеет следующее характеристическое свойство элементов — это множество треугольников с неравными сторонами.
-
Найдите дополнение: а) множества четных натуральных чисел до множества N; б) множества отрицательных чисел до множества Z; в) множества целых чисел до множества Q.
Решение: а) Дополнение к множеству четных натуральных чисел до множества N это множество нечётных натуральных чисел.
б) Дополнение к множеству отрицательных чисел до множества Z это множество неотрицательных целых чисел (N+0)или N0
в) Дополнение к множеству целых чисел до множества Q это множество дробных чисел.
Кортеж
Практические задания для самостоятельной работы
-
Сколько букв в слове «колокол»? Сколько различных букв в этом слове?
Решение: В слове колокол 7 букв, Различных букв в этом слове 3: к,о,л.
-
Запишите множество букв, с помощью которых написано слово «колокол». Запишите кортеж букв, с помощью которых написано слово «колокол».
Решение: Они образуют множество{к,о,л}. Кортеж букв <к,о,л,о,к,о,л>
-
Сколько цифр в записи числа 56 576? Сколько различных цифр в записи того же числа?
Решение: в записи числа 56 576 - 5 цифр. Различных цифр 3: 5,6,7
-
Сформулируйте задачу 3, используя понятие множества и кортежа.
Решение: Задача. Запишите множество цифр, с помощью которых написано число 56 576. Запишите кортеж цифр, с помощью которых написано число 56 576.
-
Запишите множество букв, входящих в слово «шар». Образуйте все возможные кортежи из букв, входящих в это слово.
Решение: Множество букв, входящих в слово «шар»{ш,а,р}
Все возможные кортежи: <ш>, <а>, <р>, <ш,а>, <а,р>, <ш,р>, <а,ш>, <р,а>, <р,ш>, <ш,а,р>, <а,р,ш>, <р,а,ш>, <ш,р,а>,<а,ш,р>, <р,ш,а>.
-
Являются ли данные кортежи равными?
а) <2, 1, 0, 5, 1, 9, 7, 0> и <2, 1, 0, 5, 1, 9, 7, 0>;
б) <ч, ю, д, о, в, и, щ, е> и < ч, у, д, о, в, и, щ, е>;
в) <п,а,р,а,л,л,е,л,о,г,р,а,м,м> и < п,а,р,а,л,л,е,л,о,г,р,а,м>.
Решение: а) <2, 1, 0, 5, 1, 9, 7, 0> и <2, 1, 0, 5, 1, 9, 7, 0>.
Данные кортежи являются равными, так как кортежи имеют одинаковое число компонент, т.е. одинаковую длину и каждая компонента первого кортежа равна компоненте второго кортежа с тем же номером.
б) <ч, ю, д, о, в, и, щ, е> и < ч, у, д, о, в, и, щ, е>;
Оба кортежа имеют одинаковую длину, но компонента первого кортежа под порядковым номером 2 является буква ю, а компонента второго кортежа с тем же порядковым номером буква у. ю≠у, следовательно, кортежи не равны.
в) <п,а,р,а,л,л,е,л,о,г,р,а,м,м> и < п,а,р,а,л,л,е,л,о,г,р,а,м>. Количество компонент первого кортежа – его длина равна 14, а количество компонент второго кортежа равна 13. Кортежи имеют разную длину, т.е. не равны.
Декартово произведение множеств
Практические задания для самостоятельной работы
-
Запишите все двузначные числа, цифры десятков которых принадлежат множеству А = {4, 5, 6}, а цифры единиц - множеству В= {3, 7}.
Решение: А
 В = {(4,3), (4,7), (5,3), (5,7), (6,3), (6,7)}.
В = {(4,3), (4,7), (5,3), (5,7), (6,3), (6,7)}.-
Напишите все правильные дроби, числители которых выбираются из множества {4, 3}, а знаменатель - из множества {5, 6, 7}.
Решение:
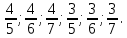
-
Перечислите элементы, принадлежащие множеству X Y, если:
Y, если:
а) X = {а, b, с}, Y = {к, l};
б) X = {a, b,c}, Y = {d};
в) X = {а, b, с}, Y=X;
г) X = {а, b, с}, Y =
 .
.Решение: а) X
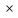 Y={(a, k), (a,l), (b, k), (b,l), (c,k),(c,l)}
Y={(a, k), (a,l), (b, k), (b,l), (c,k),(c,l)}б) X
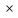
Y={(a, d), (b,d), (c, d)}
в) Y=X = {а, b, с} X
 Y={(a, a), (a,b), (a, c), (b,a), (b,b),(b,c), (c,a), (c,b), (c,c)}
Y={(a, a), (a,b), (a, c), (b,a), (b,b),(b,c), (c,a), (c,b), (c,c)}г) X = {а, b, с}, Y =
 . Следовательно, X
. Следовательно, X Y=
Y=
-
Известно, что А X В = {(2, 3), (2, 5), (2, 6), (3, 3), (3, 5),(3, 6)}. Установите, из каких элементов состоят множество А и множество В.
Решение: Так как в декартовом произведении первая компонента пары принадлежит первому множеству, а вторая компонента пары принадлежит второму множеству, то А={2,3} B={3,5,6}
-
Изобразите на координатной плоскости элементы декартова произведения множеств X и Y, если:
а) X = {-1, 0, 1, 2}, Y = {2, 3, 4};
б) X = {-1, 0, 1, 2}, Y = [2; 4];
в) X = [1; 2], Y={2, 3, 4};
г) X = [1; 7], Y = [2; 6];
д) X = [-3; 2], Y = [0; 5[;
е) Х = R, Y = [-2; 2];
ж) X = ]-3; 2[, Y = R;
з) Х = {2}, Y = R;
и) Х = R, Y={-3}.
Решение:
а) X = {-1, 0, 1, 2}, Y = {2, 3, 4}; X
 Y={(-1, 2), (-1,3), (-1,4), (0,2), (0,3), (0,4), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4)}
Y={(-1, 2), (-1,3), (-1,4), (0,2), (0,3), (0,4), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4)}
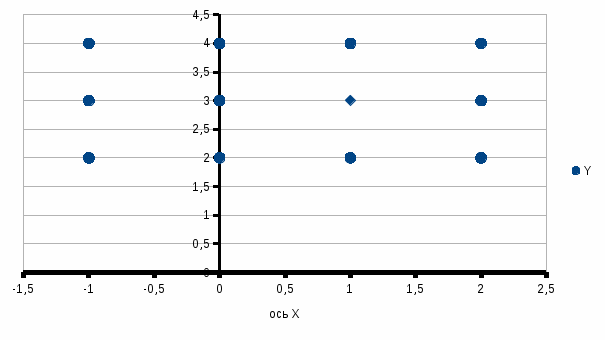
б) X = {-1, 0, 1, 2}, Y = [2; 4];
В данном примере множество Х- конечное, а множество Y – бесконечное множество действительных чисел от 2 (включая 2) до 4 (включая 4), поэтому перечислить все пары декартова произведения не представляется возможным, а результатом изображения будет четыре отрезка. Перечислим координаты концов отрезков :
(-1, 2) и (-1,4)
(0,2) и (0,4)
(1,2) и (1,4),
(2,2) и (2,4)

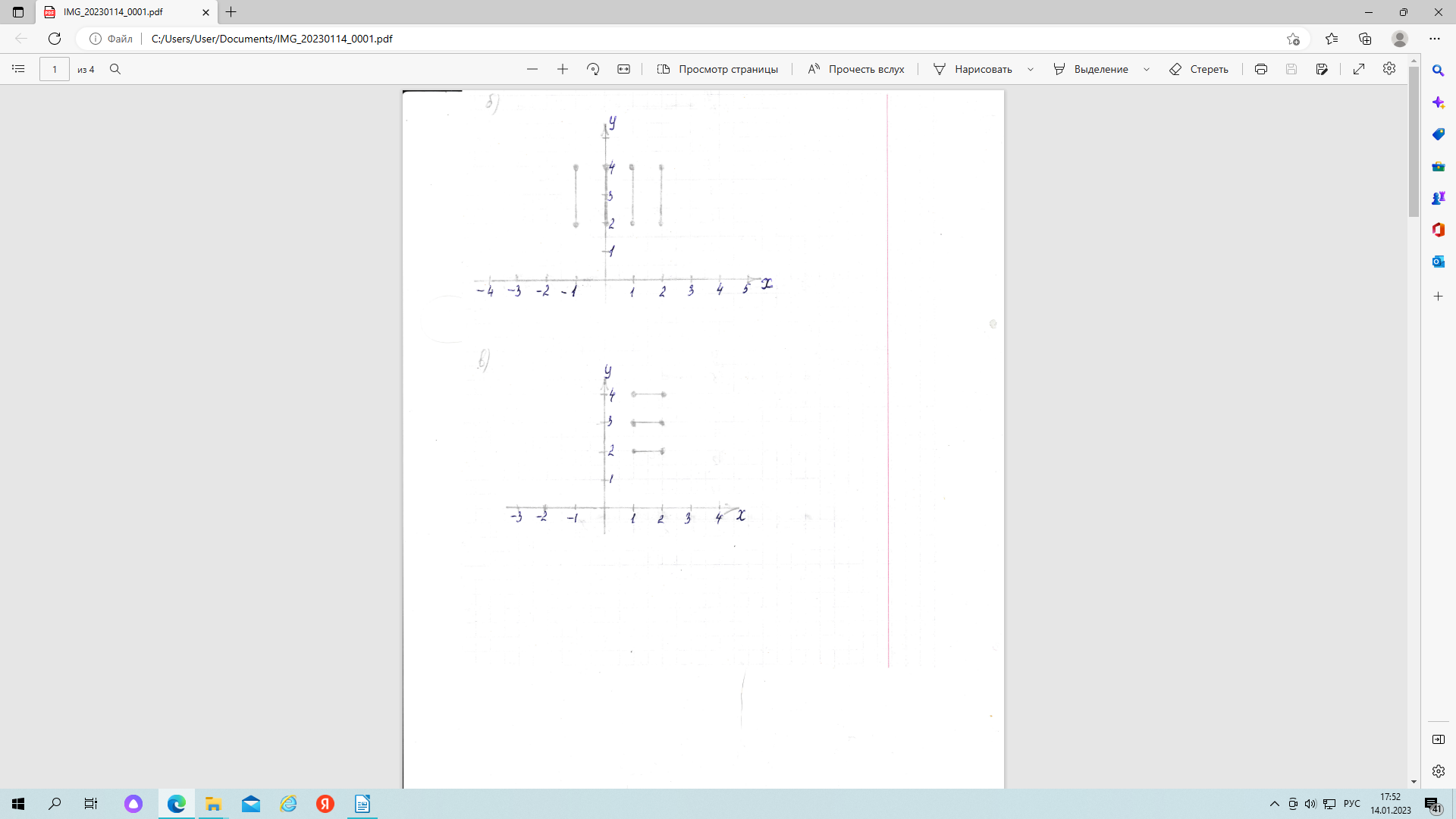
в) X = [1; 2], Y={2, 3, 4};
В данном примере множество Y- конечное, а множество Х – бесконечное множество действительных чисел от 1 (включая 1) до 2 (включая 2), поэтому перечислить все пары декартова произведения не представляется возможным, а результатом изображения будет четыре отрезка. Перечислим координаты концов отрезков
X
 Y={(1, 2), (1, 3),(1,4), (2,2), (2,3),(2,4)}
Y={(1, 2), (1, 3),(1,4), (2,2), (2,3),(2,4)}(1,2) и (2,2)
(1,3) и (2,3)
(1,4) и (2,4)

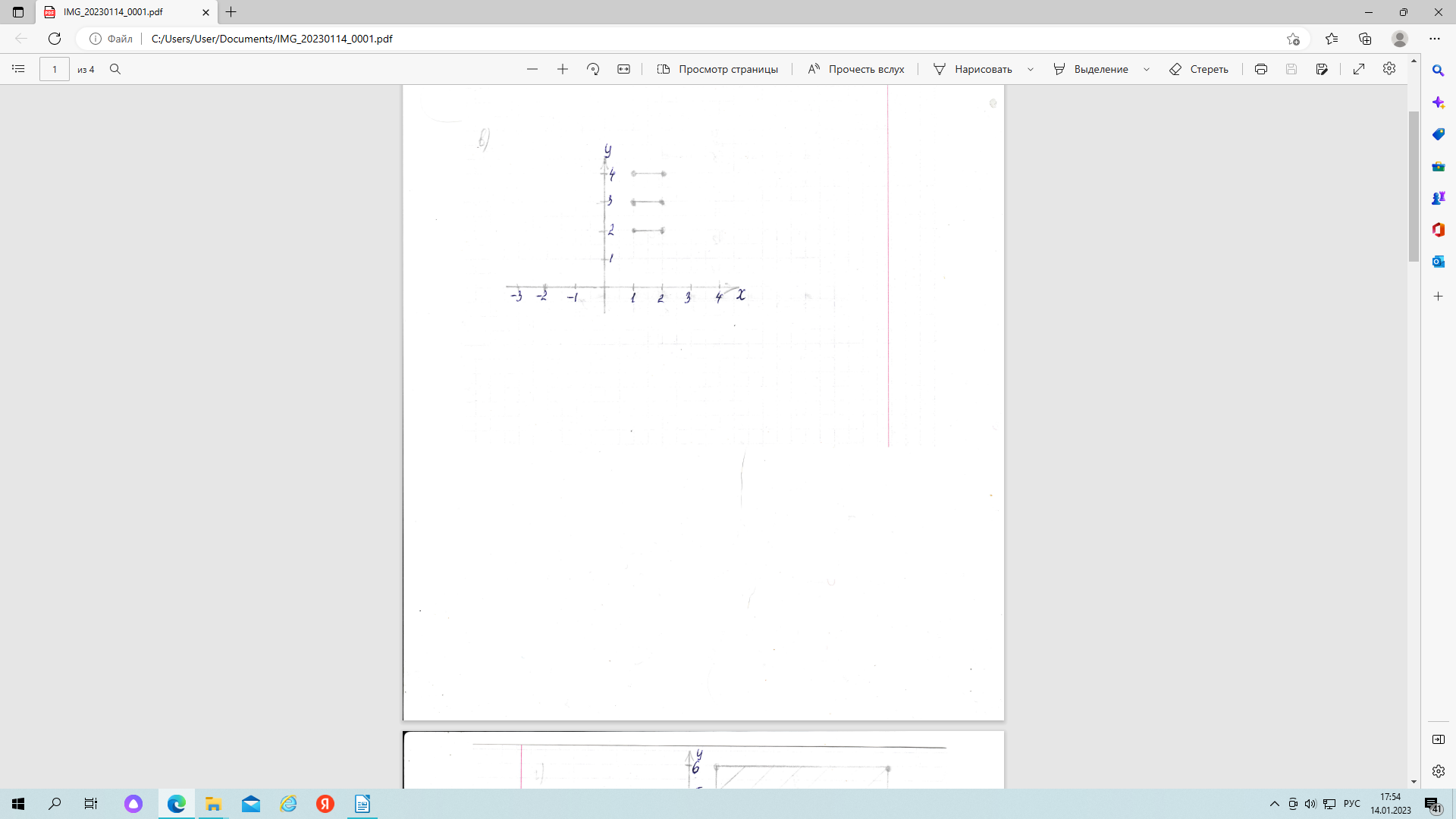
г) X = [1; 7], Y = [2; 6];
В данном примере множество Х и множество Y – это бесконечные множества действительных чисел. Результатом изображения декартова произведения будет четырехугольник. Перечислим координаты его вершин :
