(1, 2), (1,6),(7,2),(7,6).



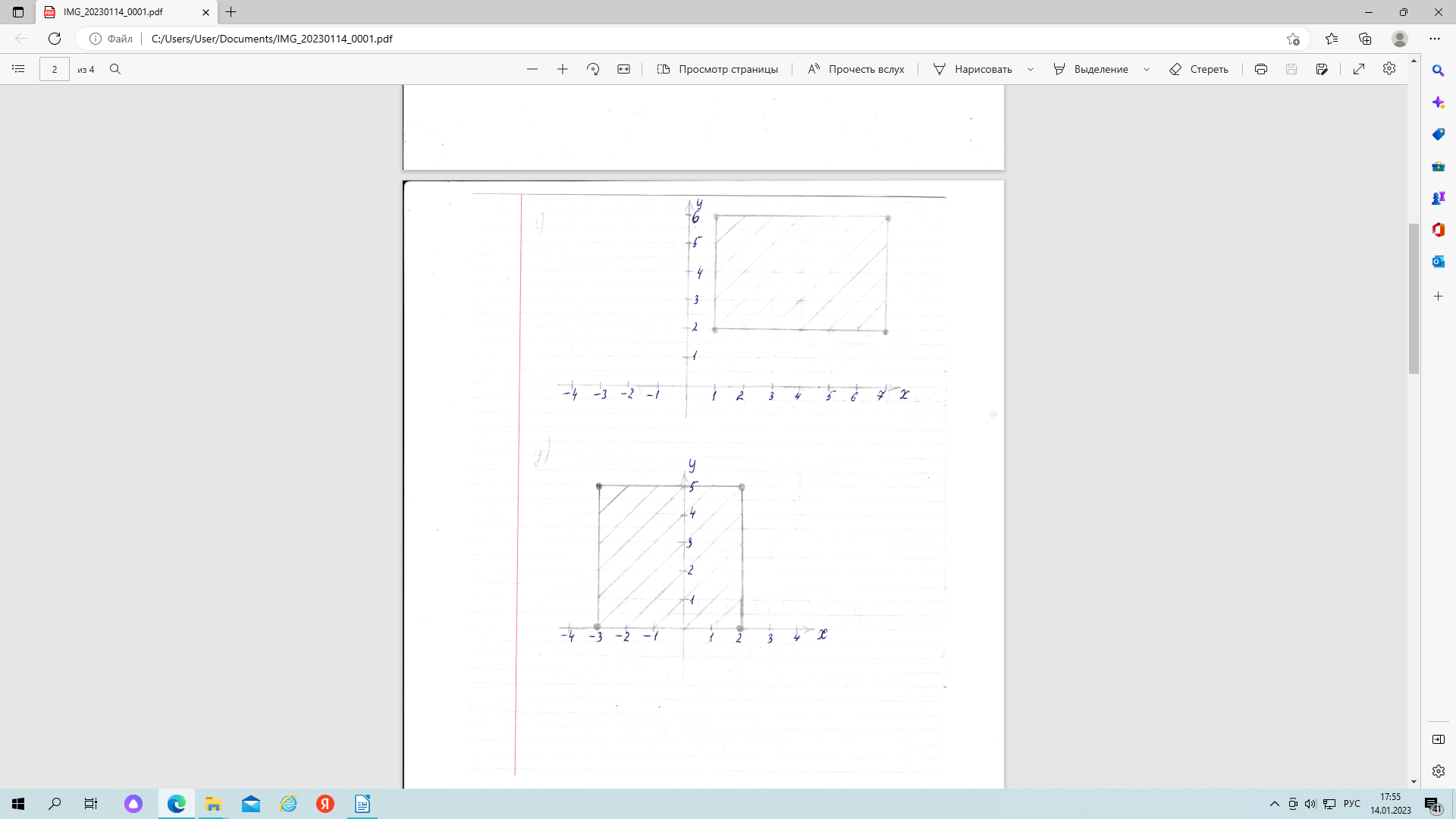
д) X = [-3; 2], Y = [0; 5[;

В данном примере множество Х и множество Y – это бесконечные множества действительных чисел. Результатом изображения декартова произведения будет четырехугольник. Перечислим координаты его вершин :

(-3,0), (-3,5),(2,0), (2,5).



е) Х = R, Y = [-2; 2];

При декартовом произведении X Y получится бесчисленное множество упорядоченных пар чисел, в которых первой компонентой может стать любое действительное число, а второй компонентой любое действительное число от -2 до 2. На координатной плоскости это множество изобразится в виде полосы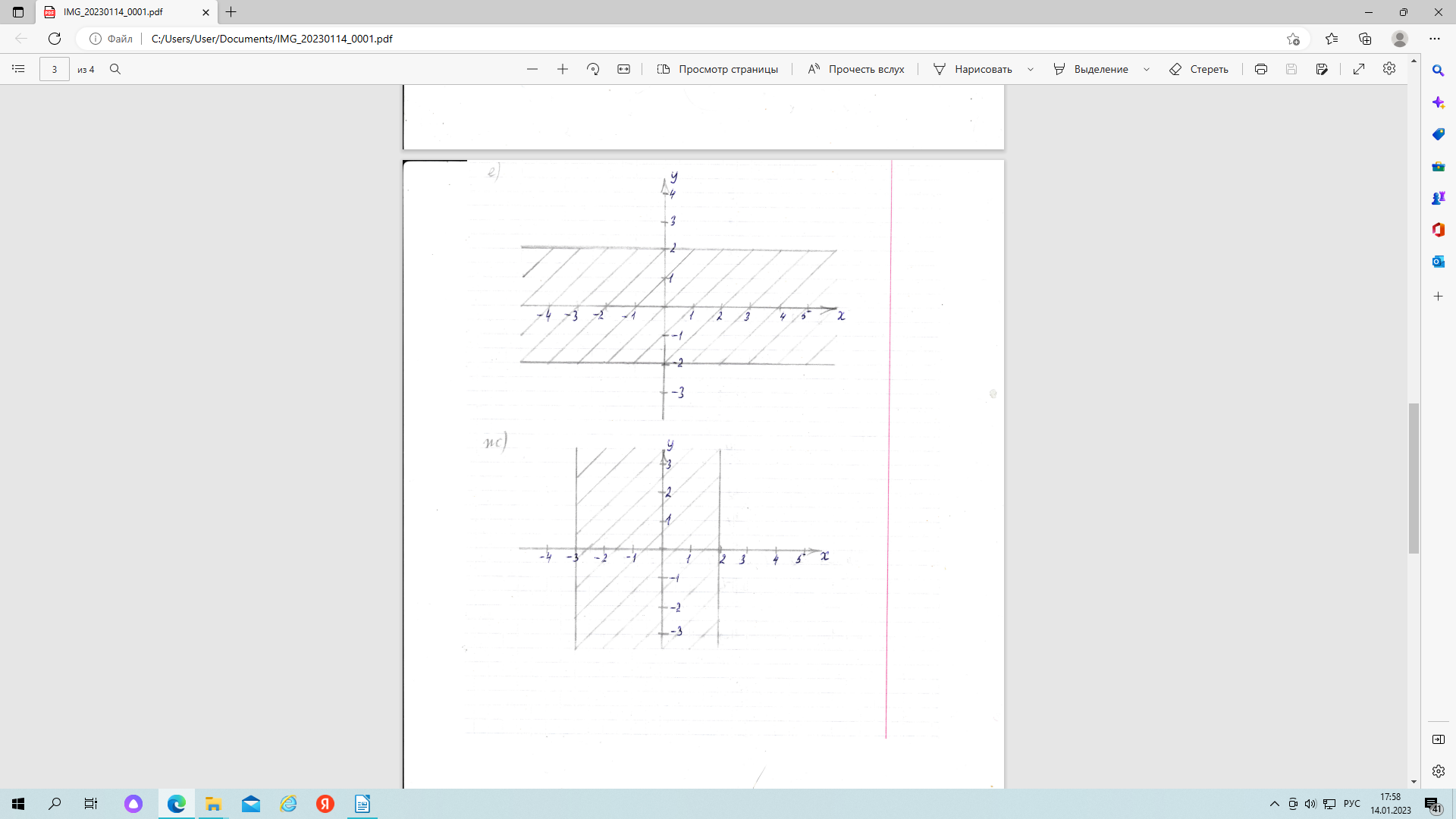



ж) X = ]-3; 2[, Y = R;

При декартовом произведении X Y получится бесчисленное множество упорядоченных пар чисел, в которых первой компонентой может стать любое действительное число от -3 до 2. , а второй компонентой любое действительное число. На координатной плоскости это множество изобразится в виде полосы




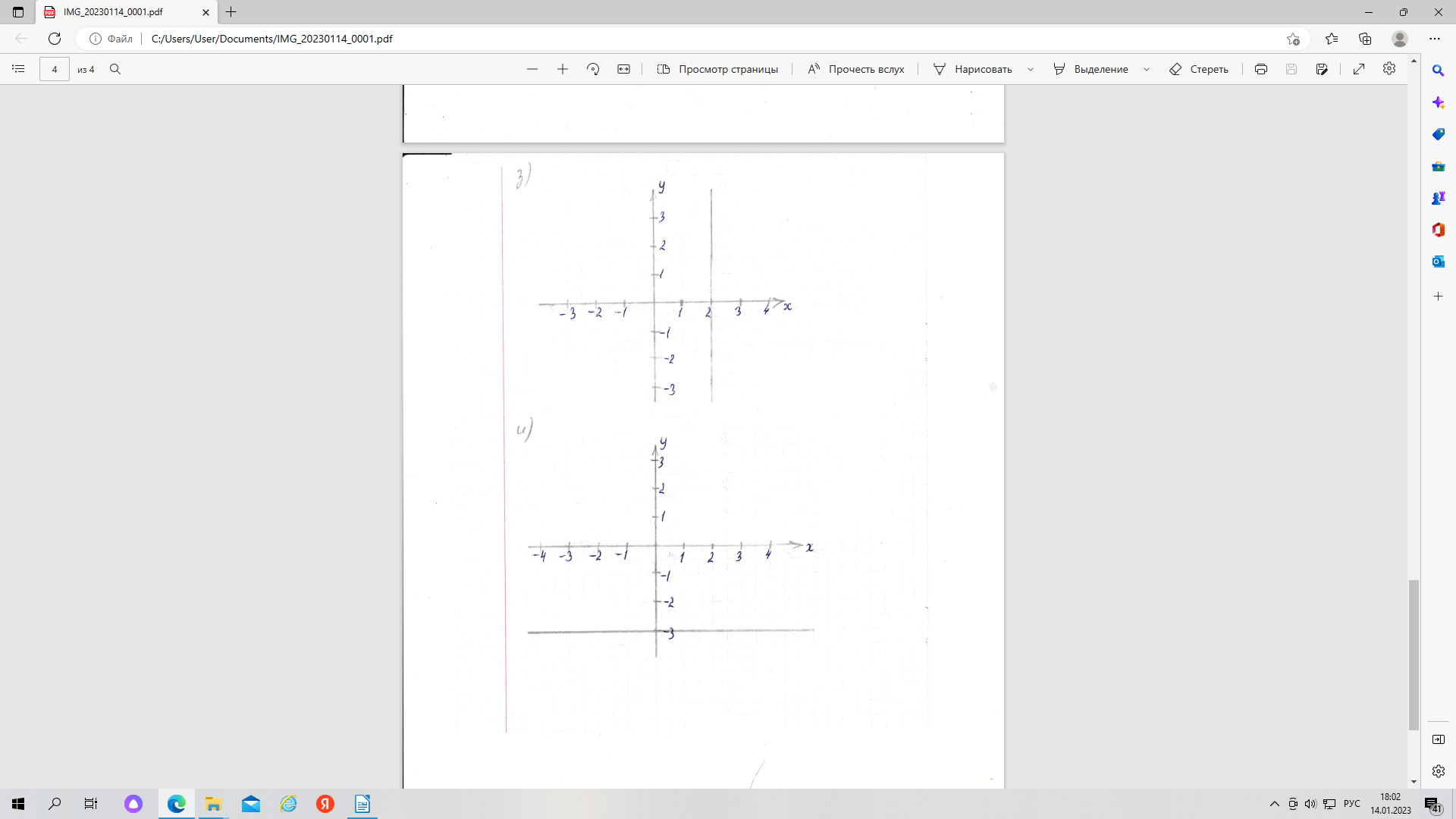
з) Х = {2}, Y = R;

В результате декартова произведения множества Х на множество Y получится бесконечное множество пар чисел, так как множество Y бесконечно. При этом первая компонента пары всегда будет равна 2. На координатной плоскости это множество изобразится в виде прямой х = 2


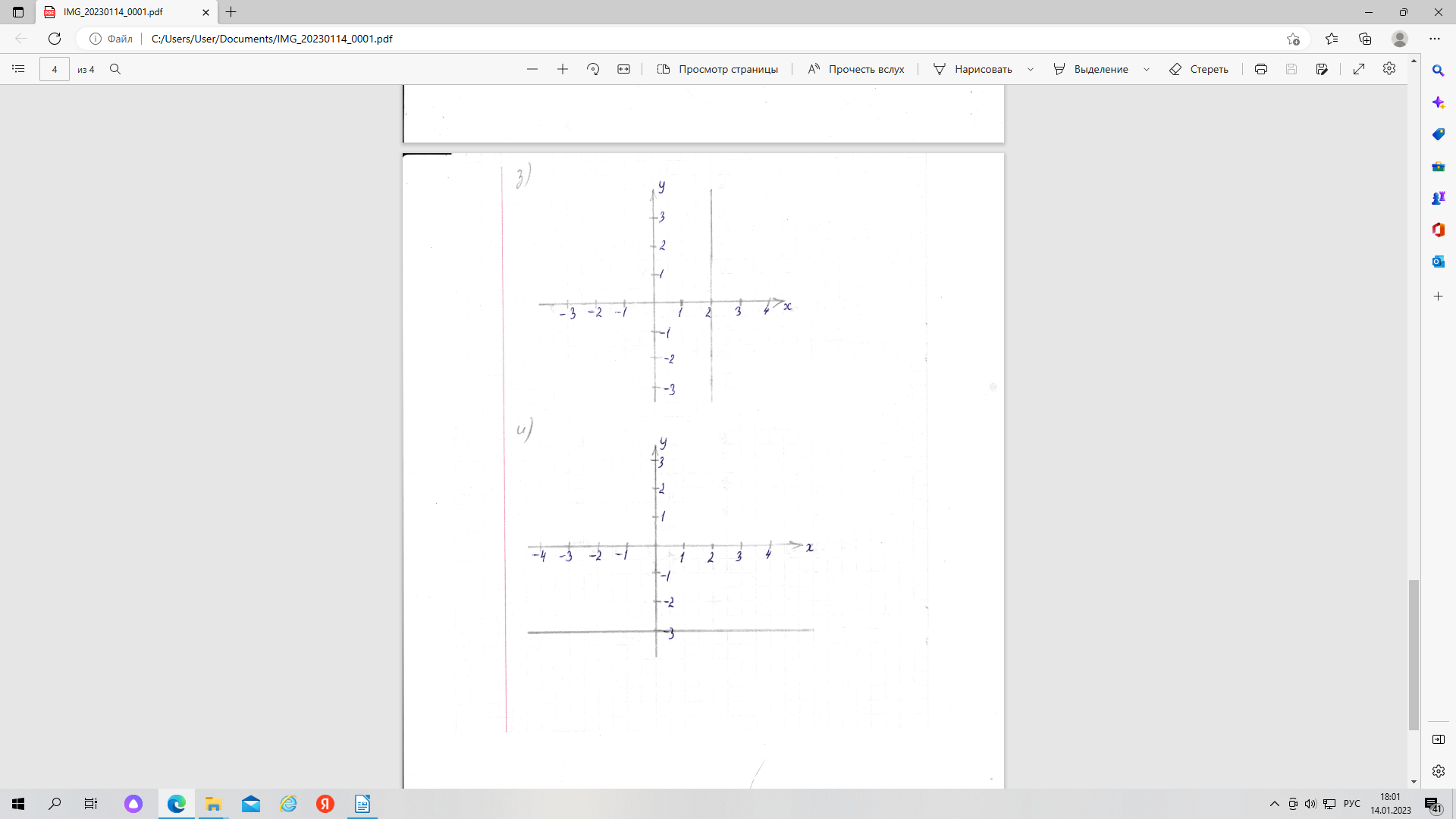
и) Х = R, Y={-3}.

В результате декартова произведения множества Х на множество Y получится бесконечное множество пар чисел, так как множество Х бесконечно. При этом вторая компонента пары всегда будет равна -3. На координатной плоскости это множество изобразится в виде прямой у = -3

---

Смотрите также файлы

• 1 мамыр азастан халытарыны бірлік, ынтыма кніне арналан сценарий.docx

• Актуальность исследования обусловлена неугасающим интересом к этапам становления и формирования основ местного самоуправления (мсу) в России и нерешенностью многим проблем, связанных с этим вопросом.docx

• Кейс 1 Орта мектепте химияны оытуды масаттары, оушылара химиялы орта білім беруді міндеттері.docx

• Индивидуальное задание по учебной практике.docx

• Цикл с постусловием.doc