ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 191
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Виды выборочного наблюдения. Способы и методы отбора единиц в выборочную совокупность.
3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли.
4. Определение объема выборочной совокупности.
Теоретический материал по теме
Вопрос 1. Теоретические основы выборочного наблюдения.
Выборочным наблюдением называется такое несплошное обследование, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность. Полученные статистические характеристики сопровождаются указанием на точность оценивания, которая зависит от репрезентативности (представительности) выбранной совокупности, т.е. от того, насколько качественно она отражает закономерность генеральной совокупности.
Генеральной совокупностью (основой выборки) называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Количество единиц генеральной совокупности обозначается через N.
Выборочная совокупность – это небольшой набор объектов, извлеченных из генеральной совокупности по определенным правилам. Количество единиц выборочной совокупности обозначается через n.
Доля выборочных единиц в объеме генеральной совокупности, выраженная в процентах, называется долей отбора (процентом выборки) и определяется следующим образом:
Например, при объеме генеральной совокупности в 2 000 единиц и выборочной в 500 единиц, говорят о 25-процентной выборке.
Единицами отбора называют элементы отбора при формировании выборочной совокупности. Единицей наблюдения выступает объект, признаки которого подлежат регистрации. Единица наблюдения может не совпадать с единицей отбора.
Если исследуется количественный признак, то непосредственной задачей выборочного наблюдения выступает оценка среднего и суммарного значений. Генеральное среднее значение определяется по данным генеральной совокупности и обозначается через . Формула для его расчета имеет вид:
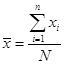
(49)
Выборочное среднее ( ) является оценкой генерального среднего и определяется по формуле:
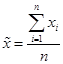 (50)
(50)Генеральная дисперсия единиц количественного признака определяется по формуле:
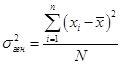 (51)
(51)Так как генеральная дисперсия по большей части в ходе исследования остается неизвестной, то условно ее принимают равной дисперсии, рассчитываемой по выборочным данным:
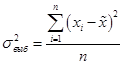 (52)
(52)При малочисленных выборках (менее 30 объектов) в формулу необходимо внести поправку – уменьшить знаменатель на единицу:
Помимо определения характеристик количественных признаков можно произвести оценку характеристик альтернативных показателей. Численность единиц, обладающих изучаемыми признаками в генеральной совокупности, обозначается через M, а в выборочной – через m. Тогда доля единиц, обладающих исследуемыми признаками в генеральной совокупности, определяется как:
где
М – численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака.
В выборочной совокупности:
где
m – численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака.
Генеральная дисперсия доли альтернативного признака рассчитывается по формуле:
где
p – генеральная доля, то есть доля единиц, обладающих определенным вариантом или вариантами изучаемого признака во всей генеральной совокупности;
q – доля единиц, не обладающих исследуемым признаком (q = 1– p).
Выборочная дисперсия доли:
, (57)
где
w – выборочная доля, то есть доля единиц, обладающих определенным вариантом или вариантами изучаемого признака в выборочной совокупности.
Основные преимущества выборочного метода по сравнению со сплошным заключаются в следующем:
1. Быстрота получения результатов обследования за счет снижения объема наблюдаемой совокупности из-за отбора и обработки данных только по определенной части ее единиц.
2. Значительное снижение стоимости наблюдения.
3. Возможность лучшей организации проведения обследования за счет минимизации влияния ошибокрегистрации в силу меньшего количества обследуемых единиц генеральной совокупности.
4. Возможность расширения программы наблюдения в силу снижения численности наблюдаемых единиц и возможности включения в программу исследования более широкого круга регистрируемых признаков.
5. Возможность использования в случаях, когда проведение сплошного наблюдения методологически невозможно. Например, при статистическом исследовании качества продукции выборочное наблюдение становится единственно возможным, так как данные виды исследования связаны с порчей или уничтожением продукции. Если генеральная совокупность объектов изучения бесконечно велика и нет возможности обследовать каждую единицу, также используется выборочный метод наблюдения (например, маркетинговые обследования покупателей, изучение пассажиропотоков и т.п.).
Наиболее существенным недостатком выборочного наблюдения является наличие ошибок репрезентативности – ситуаций, при которых выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Это может быть вызвано наличием как случайных, так и систематических ошибок репрезентативности, связанных с нарушением принципов формирования выборочной совокупности.
Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность.
Вопрос 2. Виды выборочного наблюдения. Способы и методы отбора единиц в выборочную совокупность.
В зависимости от состава и структуры генеральной совокупности различают виды выборок и способы отбора единиц.
Способ отбора единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения. Число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности неизвестен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков. Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Так, например, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Различают следующие методы отбора единиц из генеральной совокупности:
· метод индивидуального отбора, при котором в выборочную совокупность извлекаются отдельные единицы генеральной совокупности, например: при обследовании коммерческих банков – банки, при обследовании населения – конкретные люди и т.д. Применяется при организации собственно случайной, механической и типической выборок;
· метод группового отбора предполагает извлечение единиц из генеральной совокупности группами, например, бригадами, микрорайонами и т.д. Такой отбор применяется при серийной выборке;
· метод комбинированного отбора, при котором вначале отбираются группы единиц, а затем из них случайным образом извлекаются конкретные единицы совокупности.
Каждый метод отбора может быть реализован как повторным, так и бесповторным способами.
Выбор вида выборок определяется задачами исследования и, прежде всего, полнотой и особенностями информации, которой располагает исследователь об объекте наблюдения. Наиболее распространенными видами выборок, применяемыми на практике, являются:
· собственно случайная выборка;
· механическая (систематическая) выборка;
· типическая (стратифицированная, расслоенная) выборка.
Собственно случайная выборка заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков. Простая случайная выборка строится исходя из следующих правил:
1) каждый объект генеральной совокупности имеет одинаковую вероятность быть отобранным;
2) объекты отбираются независимо друг от друга.
Одним из способов извлечения случайной выборки является применение таблицы случайных чисел для получения номера каждого отобранного объекта генеральной совокупности. Сам объект затем находят в основе выборки. Таблица случайных чисел представляет собой организованную в виде таблицы последовательность чисел, в которой каждая из цифр от 0 до 9 встречается независимо друг от друга с вероятностью 1/10. Составить таблицы случайных чисел можно, например, с помощью датчика случайных чисел. Его содержат все современные статистические пакеты, а также MS Excel («Вставка функций» – «Математические» – «Случайное число»). Для проведения отбора могут быть использованы цифры любого столбца данной таблицы, при этом необходимо учитывать объем генеральной совокупности.
Для получения механической (систематической) выборки необходимо выбрать в основе выборки одну случайную начальную точку (за счет этого вносится в выборку элемент случайности) и затем производить отбор элементов в основе выборки с некоторым постоянным шагом. При таком способе отбора генеральная совокупность делится на столько групп, сколько единиц наблюдения должно войти в выборку, и из каждой группы отбирается одна единица. Единицы генеральной совокупности нумеруются числами от 1 до

