=PEARSON(массив 1; массив 2)          (75)
Параметры команды, указанные в скобочках, задаются пользователем и имеют следующее значение:

Массив 1 – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения факторного показателя x;

Массив 2 – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения результативного показателя y.
Вводить команду PEARSON можно в командной строке редактора или непосредственно в ячейке, в которой мы хотим получить значение коэффициента взаимосвязи.

Проиллюстрируем использование MS Excel для расчета взаимосвязи показателей примера 1 (таблица 49).

Исходные данные о товарообороте и количестве клиентов крупнейших туристических компаний РФ в 2011 г. оформлены в MS Excel в виде таблицы, представленной на рис. 29.


 

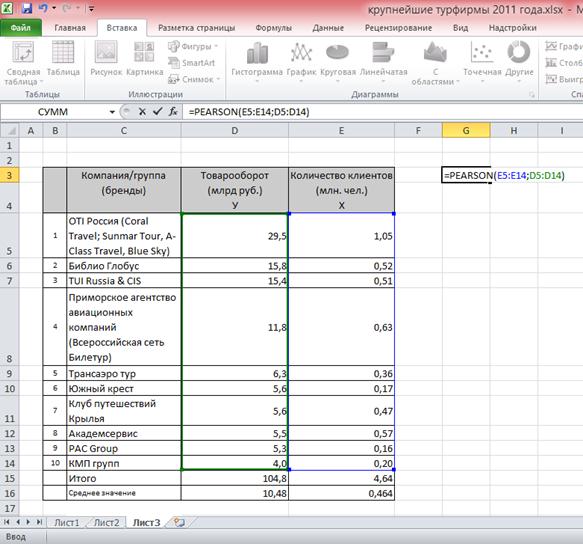
Рис. 29. Иллюстрация применения команды PEARSON в MS Excel
В этой таблице в столбце Е, а именно в ячейках с Е5 по Е14, указаны данные о количестве клиентов компаний – показатель x, а в столбце D ячейки D5:D14 содержат данные о товарообороте туркомпаний – показатель y. Очень важно проверить, чтобы формат ячеек, содержащих данные, был именно числовым, а не текстовым, поскольку текстовые и пустые ячейки при расчете коэффициента корреляции Пирсона в MS Excel не учитываются, что искажает результат вычислений и не позволяет правильно оценить взаимосвязь между показателями!

Установим курсор в ячейку G3 и воспользуемся командой PEARSON. Для этого в ячейку мы введем следующие символы: «=PEARSON(» (кавычки не вводятся!) (рис. 29). После ввода начальных символов команды MS Excel выведет на экран для подсказки внизу ячейки синтаксис формулы и будет ждать действий пользователя по заданию ее параметров. Далее произведем следующие действия:

·     для задания параметра «массив1» выделим курсором область ячеек от E5 до E14, которая содержит значения количества клиентов – факторного показателя x;

·     после этого наберем в нашей ячейке G3 или в командной строке MS Excel символ «;» (точка с запятой);

·     для задания параметра «массив2» выделим курсором область ячеек от D5 до D14, где указаны значения товарооборота туркомпаний – результативного показателя y.
Если все действия были совершены верно, то подстрочная подсказка исчезнет, а в ячейке и в командной строке MS Excel отобразится функция PEARSON с введенными пользователем параметрами (рис. 29).

---

Убедившись, что параметры команды заданы верно, нажмем на клавишу Enter и увидим (рис. 30), что в выбранной нами ячейке G3 указано значение 0,855074.

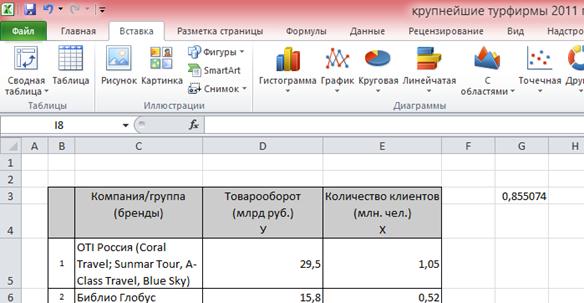
Рис. 30. Иллюстрация результата применения команды PEARSON в MS Excel
Важный момент: если нажать клавишу Enter до момента ввода параметра «массив2» или допустить ошибку при указании диапазонов данных, так что массивы получатся не равными по количеству объектов (например, в параметре «массив1» указать (E5:E14), а в «массив2» – (D6:D13)), то MS Excel вместо результата выведет в выбранной вами ячейке значение «#Н/Д».
Вопрос 2. Регрессионный анализ.

 

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (результативного признака) обусловлено влиянием одной или нескольких независимых величин (факторных признаков), и в выборе математической модели функции, при помощи которой эту взаимосвязь можно описать. Цель моделирования – получить аналитическое выражение взаимосвязи в виде математической функции, которая позволяет предсказывать значение одной переменной (признака) на основании другой.

Математическую функцию, описывающую зависимость у от х, называют уравнением регрессии, а параметры этой модели – параметрами, или коэффициентами регрессии.

Уравнение регрессии описывает теоретическую линию, вокруг которой концентрируются точки на диаграмме рассеяния и которая определяет основное направление взаимосвязи между признаками x и у. (рис. 31).

Рис. 31. Диаграмма рассеяния (поле корреляции)
Для построения уравнения регрессии необходимо выполнение следующих требований:

·     факторный и результативный признаки должны иметь количественное выражение;

·     совокупность исходных данных должна быть однородной, значительной по объему и математически описываться непрерывной функцией;

·     взаимосвязи между явлениями должны описываться линейной или приводимой к линейной форме зависимостью.
Соблюдение данных требований позволяет построить статистическую модель, наилучшим образом описывающую взаимосвязь между признаками.

---

Парная линейная регрессия позволяет получить аналитическое выражение связи между двумя признаками – результативным и факторным, описываемое уравнением прямой линии.

Уравнение парной линейной регрессии имеет вид:
,          (76)

где

 – расчетное значение результативного признака y при определенном значении факторного признака x;

а₀ показывает усредненное влияние на результативный признак не учтенных в уравнении факторных признаков;

а₁ – коэффициент регрессии, показывающий, насколько в среднем изменится значение результативного признака при изменении факторного на единицу собственного измерения.
Определить тип уравнения можно, исследуя зависимость графически. Существуют другие способы, позволяющие определить вид уравнения связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, между ними существует линейная связь, а при обратной зависимости – гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая, или степенная регрессия.

Оценка параметров уравнения регрессии a₀ и a₁ осуществляется методом наименьших квадратов. Этот метод позволяет найти такие параметры модели, при которых расчетные значения  были бы максимально близки к исходным значениям у. Поскольку в статистке за меру отличия чаще всего принимается отклонение, то методом наименьших квадратов находятся параметры модели, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по линейному уравнению регрессии.

Для нахождения параметров линейной парной регрессии методом наименьших квадратов необходимо решить систему нормальных уравнений, которая имеет следующий вид:

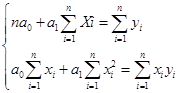           (78)

где

n – объем исследуемой совокупности (число единиц наблюдения);

x_i, у_i – значения факторного и результативного признаков у i-й единицы.
Рассчитать параметры линейного уравнения регрессии можно при помощи стандартного табличного редактора MS Excel.

---

Для начала напомним, что с точки зрения математики линейная функция – это прямая линия, которая проходит в двумерной системе координат. Параметр a₀ – это точка, в которой прямая линия пересекает ось y, т.е. в этой точке значение х = 0. За расположение прямой в системе координат отвечает угол наклона прямой линии (отношение величины подъема линии к ее длине), а именно – параметр a₁: если наклон имеет знак «+», то линия поднимается слева на право, если наклон равен «0» – линия идет горизонтально оси х, а если знак «-», то линия опускается слева на право.

В MS Excel существует встроенная функция «НАКЛОН», которая позволяет легко получить значение коэффициента a₁ по исходным данным y и х методом наименьших квадратов.

Синтаксис этой команды имеет следующий вид:
=НАКЛОН(известные значения_y; известные значения_х)            (79)
Параметры команды, указанные в скобочках, задаются пользователем и имеют следующее значение:

Известные значения_y– диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения результативного показателя y;

Известные значения_х – диапазон данных в исходной таблице, как правило в столбце, в котором указаны значения факторного показателя x.
Диапазоны данных задаются пользователем и очень важно сделать это правильно, поскольку, например, перепутав местами диапазоны х и y, Вы дадите программе команду вычислять коэффициент регрессии уже для другого случая взаимосвязи – исследования влияния значений y на значения х, что не входит в наши планы и неверно, поскольку y будет рассматриваться программой как факторный признак, а не как признак-результат.

Расчет параметра a₀ в среде MS Excel также упрощается. Для начала необходимо рассчитать средние значения показателей y и х, вычислить параметр a₁, а затем произвести расчет параметра a₀ по следующей формуле:

         (80)
Таким образом, расчет параметров уравнения регрессии при помощи MS Excel зависит от точности действий пользователя при вводе исходных данных и задании параметров специальной встроенной для этого команды-функции.

 

Пример 2. Быстродействие компьютеров, объединенных в сеть, при

---

возникновении перегрузок, как правило, снижается. Естественно, чем больше загрузка компьютера x, тем большим должно быть время реакции y. Под временем реакции понимается интервал с момента нажатия клавиши Enter до момента выдачи компьютером ответа на введенный вами запрос.
Таблица 50.

 

Показатели быстродействия компьютера

 

Время реакции компьютера, сек.	Загрузка компьютера от полной его мощности, %
0,31	20,2
0,69	22,7
2,27	41,7
0,57	24,6
1,28	20,0
0,88	39,0
2,11	33,4
4,84	63,9
1,60	35,8
5,06	62,3

Предположим наличие линейной зависимости между рассматриваемыми показателями. Построим расчетную таблицу для определения параметров линейного уравнения регрессии времени реакции компьютера (табл. 51).
Таблица 51.

 

Расчетная таблица для определения параметров уравнения регрессии между временем реакции и процентом загрузки компьютера от полной мощности

 

№ п.п.	Время реакции компьютера (сек), y	Загрузка компьютера (%), х	х2	xy
1.	0,31	20,2	408,04	6,26	0,38
2.	0,69	22,7	515,29	15,66	0,63
3.	2,27	41,7	1738,89	94,66	2,53
4.	0,57	24,6	605,16	14,02	0,82
5.	1,28	20,0	400,00	25,60	0,36
6.	0,88	39,0	1521,00	34,32	2,26
7.	2,11	33,4	1115,56	70,47	1,70
8.	4,84	63,9	4083,21	309,28	4,75
9.	1,60	35,8	1281,64	57,28	1,94
10.	5,06	62,3	3881,29	315,24	4,59
Итого	19,61	363,6	15550,08	942,79	-

---

Смотрите также файлы

• Классный частренинг Мотивация учения.pdf

• 2. Письменно ответьте на вопросы Понятие об антропогенном кризисе и катастрофе.doc

• Решение Определим фондоотдачу (фотд) Фотд 42000 16000 2,625 тыс руб.docx

• Методические указания по выполнению лабораторной работы по дисциплине Теплофизика для студентов направления 20. 03. 01 Техносферная безопасность.pdf

• Фгбоу во ниу мэи.docx