ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 185
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
оборотным капиталом и выбора источника финансирования;
· способность рассчитывать парный линейный коэффициент корреляции и делать по нему выводы;
· способность рассчитывать параметры линейного и нелинейного уравнения регрессии;
· способность интерпретировать коэффициенты регрессии и эластичности.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· корреляционный анализ;
· регрессионный анализ;
· линейный коэффициент корреляции Пирсона;
· уравнение регрессии;
· коэффициент регрессии;
· парная линейная регрессия;
· теоретическое корреляционное отношение;
· коэффициент эластичности.
Вопросы темы:
1. Корреляционный анализ.
2. Регрессионный анализ.
Теоретический материал по теме
Вопрос 1. Корреляционный анализ.
Корреляционный анализ используется для количественного определения тесноты и направления связи между признаками при помощи коэффициента корреляции. Знаки при коэффициенте корреляции характеризуют направление связи между изучаемыми признаками, а по его значению характеризуют силу или тесноту связи между признаками. Корреляционный анализ дает ответы на следующие вопросы:
· существует ли между рассматриваемыми признаками взаимосвязь вообще?
· если связь существует, то каково ее направление: значения результативного признака растут или уменьшаются под влиянием факторного?
· насколько тесной является эта взаимосвязь?
Для проведения корреляционного анализа необходимо выполнение следующих условий:
1. Признаки, между которыми исследуется взаимосвязь, должны иметь количественное выражение, т.е. каждая единица совокупности должна характеризоваться двумя числами – значением факторного и значением результативного признаков.
2. Данные по каждому признаку должны иметь одинаковую размерность и методологию расчета. Например, изучая зависимость заработной платы сотрудника от стажа его работы, нельзя, чтобы у части сотрудников стаж был указан в месяцах, а у части – в годах, или у одних брался номинальный (до вычета налогов), а у других – реальный размер заработной платы. В данных не должно быть пропусков (например, неизвестен стаж хотя бы у одного сотрудника). Единицы, имеющие пропуски в значениях факторного или результативного признаков, исключаются из исходных данных.
3. Рассматриваемая совокупность должна быть однородна по составу единиц и существенна по их количеству. Например, качество анализа будет выше, если рассматривать взаимосвязь зарплаты и стажа по категориям сотрудников (вспомогательные работники, рабочие, административный персонал, менеджеры и т.п.), используя данные как можно большего числа сотрудников каждой категории.
Если по аналитическому выражению связь между признаками можно описать уравнением прямой, для выявления наличия, направленности и тесноты связи рассчитывают линейный коэффициент корреляции.
Линейный коэффициент корреляции Пирсона, обозначаемый r, характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости.
Линейный коэффициент корреляции изменяется в пределах от -1 до +1: . Корреляция, равная 1, указывает на идеальную взаимосвязь в виде прямой линии, причем более высокие значения одной переменной соответствуют предсказуемым более высоким значениям другой переменной. Корреляция, равная -1, указывает на отрицательную идеальную взаимосвязь в виде прямой линии, причем одна переменная уменьшается с ростом другой.
Абсолютное значение коэффициента корреляции указывает на силу взаимосвязи, а знак (+ или -) указывает направление (увеличение или уменьшение) связи. В таблице 47 показано, как следует интерпретировать связь в каждом конкретном случае.
Таблица 47.
Интерпретация значения линейного коэффициента корреляции
Расчет линейного коэффициента корреляции осуществляется по формуле:
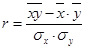, (73)
где
;
;
;
;
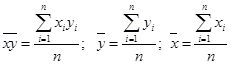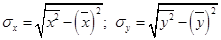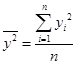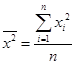n – число наблюдений.
Вычисление линейного коэффициента корреляции удобно проводить при помощи вспомогательной таблицы (табл. 48):
Таблица 48.
Вспомогательная таблица для расчета линейного коэффициента корреляции
Если преобразовать формулу 73, то линейный коэффициент корреляции можно вычислить, используя итоговые суммы из таблицы 48:
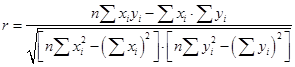(74)
Числитель выражает взаимодействие двух переменных и определяет знак корреляции. Если между переменными существует сильная положительная взаимосвязь, числитель примет положительное значение, если сильная обратная – числитель примет отрицательное значение. Знаменатель формул 73 и 74 всегда положителен, т.к. он является произведением средних квадратических отклонений по X и Y, которые всегда больше нуля, т.к. рассчитываются как квадратный корень из дисперсии.
Пример 1. Определим тесноту взаимосвязи между величиной товарооборота и количеством обслуженных клиентов десяти крупнейших туристических компаний/групп по итогам 2011 г. (по данным kommersant.ru, табл. 49).
Таблица 49.
Показатели деятельности крупнейших туристических компаний/групп по итогам 2011 г.
(по данным kommersant.ru)
Диаграмма рассеяния, представленная на рис. 28, отображает положительную по направлению и близкую к линейной взаимосвязь между товарооборотом компаний (результативный признак y) и количеством обслуженных клиентов (факторный признак x) – точки на графике поднимаются вверх при движении по оси x, ось области концентрации облака точек имеет вид, наиболее близкий по форме к прямой линии.
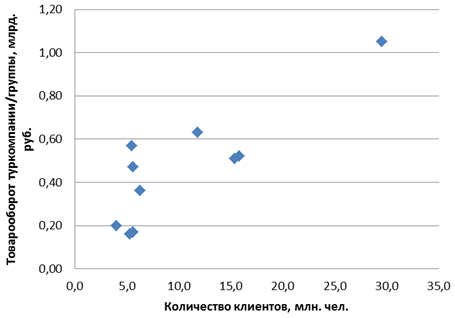
Рис. 28. Диаграмма рассеяния, характеризующая взаимосвязь между величиной товарооборота и количеством обслуженных клиентов наиболее крупных по итогам 2011 г. туристических компаний/групп
Подтвердим предположение о наличии положительной связи на основании расчета линейного коэффициента корреляции.
1. Используя формулу (73), получаем:
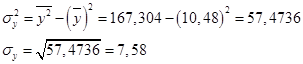
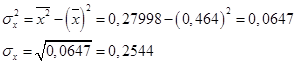
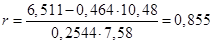
2. По формуле (74) значение коэффициента корреляции составило:
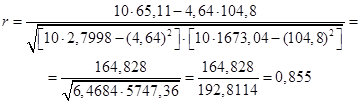
Таким образом, можно сделать вывод, что между величиной товарооборота туристической компании и количеством обслуженных ею клиентов существует сильная по тесноте и прямая по направлению взаимосвязь.
Существенно облегчить и ускорить расчет показателей взаимосвязи позволяет широко распространенный стандартный табличный редактор MS Excel. Для расчета величины парного линейного коэффициента корреляции Пирсона необходимо в редакторе данных построить таблицу с исходными значениями анализируемых показателей и ввести вручную или вызвать с помощью меню специальную команду-функцию PEARSON.
Синтаксис этой команды имеет следующий вид:
· способность рассчитывать парный линейный коэффициент корреляции и делать по нему выводы;
· способность рассчитывать параметры линейного и нелинейного уравнения регрессии;
· способность интерпретировать коэффициенты регрессии и эластичности.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· корреляционный анализ;
· регрессионный анализ;
· линейный коэффициент корреляции Пирсона;
· уравнение регрессии;
· коэффициент регрессии;
· парная линейная регрессия;
· теоретическое корреляционное отношение;
· коэффициент эластичности.
Вопросы темы:
1. Корреляционный анализ.
2. Регрессионный анализ.
Теоретический материал по теме
Вопрос 1. Корреляционный анализ.
Корреляционный анализ используется для количественного определения тесноты и направления связи между признаками при помощи коэффициента корреляции. Знаки при коэффициенте корреляции характеризуют направление связи между изучаемыми признаками, а по его значению характеризуют силу или тесноту связи между признаками. Корреляционный анализ дает ответы на следующие вопросы:
· существует ли между рассматриваемыми признаками взаимосвязь вообще?
· если связь существует, то каково ее направление: значения результативного признака растут или уменьшаются под влиянием факторного?
· насколько тесной является эта взаимосвязь?
Для проведения корреляционного анализа необходимо выполнение следующих условий:
1. Признаки, между которыми исследуется взаимосвязь, должны иметь количественное выражение, т.е. каждая единица совокупности должна характеризоваться двумя числами – значением факторного и значением результативного признаков.
2. Данные по каждому признаку должны иметь одинаковую размерность и методологию расчета. Например, изучая зависимость заработной платы сотрудника от стажа его работы, нельзя, чтобы у части сотрудников стаж был указан в месяцах, а у части – в годах, или у одних брался номинальный (до вычета налогов), а у других – реальный размер заработной платы. В данных не должно быть пропусков (например, неизвестен стаж хотя бы у одного сотрудника). Единицы, имеющие пропуски в значениях факторного или результативного признаков, исключаются из исходных данных.
3. Рассматриваемая совокупность должна быть однородна по составу единиц и существенна по их количеству. Например, качество анализа будет выше, если рассматривать взаимосвязь зарплаты и стажа по категориям сотрудников (вспомогательные работники, рабочие, административный персонал, менеджеры и т.п.), используя данные как можно большего числа сотрудников каждой категории.
Если по аналитическому выражению связь между признаками можно описать уравнением прямой, для выявления наличия, направленности и тесноты связи рассчитывают линейный коэффициент корреляции.
Линейный коэффициент корреляции Пирсона, обозначаемый r, характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости.
Линейный коэффициент корреляции изменяется в пределах от -1 до +1: . Корреляция, равная 1, указывает на идеальную взаимосвязь в виде прямой линии, причем более высокие значения одной переменной соответствуют предсказуемым более высоким значениям другой переменной. Корреляция, равная -1, указывает на отрицательную идеальную взаимосвязь в виде прямой линии, причем одна переменная уменьшается с ростом другой.
Абсолютное значение коэффициента корреляции указывает на силу взаимосвязи, а знак (+ или -) указывает направление (увеличение или уменьшение) связи. В таблице 47 показано, как следует интерпретировать связь в каждом конкретном случае.
Таблица 47.
Интерпретация значения линейного коэффициента корреляции
| Значение r | Характеристика связи | Интерпретация связи | Наглядное представление связи |
| r = 0 | Взаимосвязь отсутствует | - | Совершенно случайное облако, не имеющее ориентации ни вверх, ни вниз при движении вправо |
| Близко к 0, но > 0 | незначительная положительная взаимосвязь | С увеличением факторного признака слабо возрастает результативный признак | Точки данных образуют случайное облако с незначительной ориентацией вверх и вправо |
| Близко к 1 | сильная положительная взаимосвязь | С увеличением факторного признака увеличивается результативный признак | Точки данных довольно плотно сгруппированы (с небольшим разбросом) вокруг прямой линии, направленной вверх и вправо |
| Близко к 0, но < 0 | незначительная отрицательная взаимосвязь | С увеличением факторного признака незначительно уменьшается результативный – и наоборот | Точки данных образуют случайное облако с незначительной ориентацией вниз и вправо |
| Близко к -1 | сильная отрицательная взаимосвязь | С увеличением факторного признака уменьшается результативный, и наоборот | Точки данных довольно плотно сгруппированы (с небольшим разбросом) вокруг прямой линии, направленной вниз и вправо |
| r = 1 | функциональная | Определенному значению факторного признака соответствует строго одно значение результативного | Идеальная положительная взаимосвязь: все точки данных располагаются строго на прямой линии, направленной вверх и вправо |
| r = -1 | Идеальная отрицательная взаимосвязь: все точки данных располагаются строго на прямой линии, направленной вниз и вправо |
Расчет линейного коэффициента корреляции осуществляется по формуле:
, (73)где
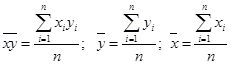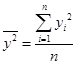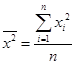; ; ; ;n – число наблюдений.
Вычисление линейного коэффициента корреляции удобно проводить при помощи вспомогательной таблицы (табл. 48):
Таблица 48.
Вспомогательная таблица для расчета линейного коэффициента корреляции
| № объекта, n | Факторный признак, хi | Результативный признак, yi | yi2 (гр. 3 * гр. 3) | xi2 (гр. 2 *гр. 2) | xiyi (гр. 2 *гр. 3) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | x1 | y1 | y12 | x12 | x1∙y1 |
| 2 | x2 | y2 | y22 | x22 | x2∙y2 |
| … | … | … | … | … | … |
| n | Xn | Yn | Yn2 | Xn2 | Xn∙Yn |
| Итого |  |  |  |  |  |
| Среднее значение |  |  |  |  |  |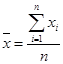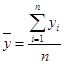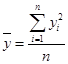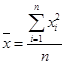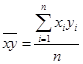
Если преобразовать формулу 73, то линейный коэффициент корреляции можно вычислить, используя итоговые суммы из таблицы 48:
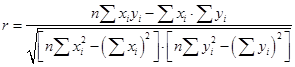(74)Числитель выражает взаимодействие двух переменных и определяет знак корреляции. Если между переменными существует сильная положительная взаимосвязь, числитель примет положительное значение, если сильная обратная – числитель примет отрицательное значение. Знаменатель формул 73 и 74 всегда положителен, т.к. он является произведением средних квадратических отклонений по X и Y, которые всегда больше нуля, т.к. рассчитываются как квадратный корень из дисперсии.
Пример 1. Определим тесноту взаимосвязи между величиной товарооборота и количеством обслуженных клиентов десяти крупнейших туристических компаний/групп по итогам 2011 г. (по данным kommersant.ru, табл. 49).
Таблица 49.
Показатели деятельности крупнейших туристических компаний/групп по итогам 2011 г.
(по данным kommersant.ru)
| № п.п. | Компания/группа (бренды) | Товарооборот (млрд руб.) y | Количество клиентов (млн. чел.), x | Расчетные графы | ||
| у2 | х2 | ху | ||||
| 1. | OTI Россия (Coral Travel; Sunmar Tour, A-Class Travel, Blue Sky) | 29,5 | 1,05 | 870,25 | 1,1025 | 30,98 |
| 2. | «Библио-Глобус» | 15,8 | 0,52 | 249,64 | 0,2704 | 8,22 |
| 3. | TUI Russia & CIS | 15,4 | 0,51 | 237,16 | 0,2601 | 7,85 |
| 4. | Приморское агентство авиационных компаний (Всероссийская сеть «БИЛЕТУР») | 11,8 | 0,63 | 139,24 | 0,3969 | 7,43 |
| 5. | Трансаэро Тур | 6,3 | 0,36 | 39,69 | 0,1296 | 2,27 |
| 6. | «Южный крест» | 5,6 | 0,17 | 31,36 | 0,0289 | 0,95 |
| 7. | Клуб путешествий «Крылья» | 5,6 | 0,47 | 31,36 | 0,2209 | 2,63 |
| 8. | Академсервис | 5,5 | 0,57 | 30,25 | 0,3249 | 3,14 |
| 9. | PAC Group | 5,3 | 0,16 | 28,09 | 0,0256 | 0,85 |
| 10. | «КМП групп» | 4,0 | 0,20 | 16,00 | 0,0400 | 0,80 |
| Итого | 104,8 | 4,64 | 1 673,04 | 2,7998 | 65,11 | |
| Среднее значение | 10,48 | 0,464 | 167,304 | 0,27998 | 6,511 | |
Диаграмма рассеяния, представленная на рис. 28, отображает положительную по направлению и близкую к линейной взаимосвязь между товарооборотом компаний (результативный признак y) и количеством обслуженных клиентов (факторный признак x) – точки на графике поднимаются вверх при движении по оси x, ось области концентрации облака точек имеет вид, наиболее близкий по форме к прямой линии.
Рис. 28. Диаграмма рассеяния, характеризующая взаимосвязь между величиной товарооборота и количеством обслуженных клиентов наиболее крупных по итогам 2011 г. туристических компаний/групп
Подтвердим предположение о наличии положительной связи на основании расчета линейного коэффициента корреляции.
1. Используя формулу (73), получаем:
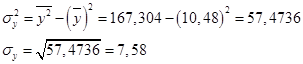
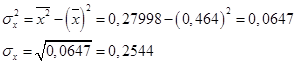
2. По формуле (74) значение коэффициента корреляции составило:
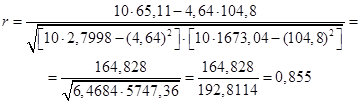
Таким образом, можно сделать вывод, что между величиной товарооборота туристической компании и количеством обслуженных ею клиентов существует сильная по тесноте и прямая по направлению взаимосвязь.
Существенно облегчить и ускорить расчет показателей взаимосвязи позволяет широко распространенный стандартный табличный редактор MS Excel. Для расчета величины парного линейного коэффициента корреляции Пирсона необходимо в редакторе данных построить таблицу с исходными значениями анализируемых показателей и ввести вручную или вызвать с помощью меню специальную команду-функцию PEARSON.
Синтаксис этой команды имеет следующий вид: