ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 244
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В качестве группировочного возьмем признак «размер страховых премий». Образуем четыре группы страховых компаний с равными интервалами. Величину интервала определим по формуле (3):
Согласно правилам округления в качестве ширины интервала возьмем величину 23. Обозначим границы групп:
| 1-я группа – 4,6–27,6 | 3-я группа – 50,6–73,6 |
| 2-я группа – 27,6–50,6 | 4-я группа – 73,6–96,6 |
Теперь необходимо подсчитать количество страховых компаний в каждой группе. В 1-ю группу войдут 23 компании (№№ от 30 до 8 включительно по исходным данным табл. 8), во 2-ю – три компании (№№ 7–5), в 3-ю – две (№№ 4–3) и в 4-ю – две (№№ 2–1).
Поскольку единичные и пустые группы в нашей группировке не обнаружены, можем переходить к завершающему этапу – построению итоговой группировочной таблицы, в которой все показатели будут приведены в разрезе построенных нами групп, а не по индивидуальным страховым компаниям, как в исходных данных. Для этого нужно просто суммировать индивидуальные значения показателей страховых компаний «страховые выплаты» и «количество заключенных договоров» по каждой группе и записать полученные суммы в соответствующие строки и столбцы итоговой таблицы (табл. 9).
Таблица 9.
Группировка крупнейших страховых компаний РФ по величине полученных страховых премий за 2012 год
| Группы страховых компаний по величине страховых премий, млрд руб. | Число страховых компаний | Страховые выплаты, млрд руб. | Количество заключенных договоров, млн шт. |
| А | 1 | 2 | 3 |
| 4,6–27,6 | 23 | 111,8 | 43,66 |
| 27,6–50,6 | 3 | 51,4 | 12,53 |
| 50,6–73,6 | 2 | 72,1 | 13,25 |
| 73,6–96,6 | 2 | 71,0 | 27,87 |
| Итого | 30 | 306,3 | 97,31 |
Структурная группировка страховых организаций на основе данных таблицы 9 будет иметь вид:
Таблица 10.
Группировка крупнейших страховых компаний РФ по величине полученных страховых премий за 2012 год
| Группы страховых компаний по величине страховых премий, млрд руб. | Число страховых компаний | Страховые выплаты, % от общего размера | Количество заключенных договоров, % от общего размера |
| А | 1 | 2 | 3 |
| 4,6–27,6 | 23 | 36,50 | 44,87 |
| 27,6–50,6 | 3 | 16,78 | 12,88 |
| 50,6–73,6 | 2 | 23,54 | 13,62 |
| 73,6–96,6 | 2 | 23,18 | 28,64 |
| Итого | 30 | 100,00 | 100,00 |
Из таблицы 10 видно, что больше трети (36,50 %) всех страховых выплат и чуть менее половины всех заключенных договоров (44,87 %) приходится на группы страховых компаний с объемом страховых премий от 4,6 до 27,6 млрд руб.
Аналитическая группировка (табл. 11) показывает, что размер страховых премий и количество заключенных договоров находятся между собой в прямой зависимости. А вот величина страховых выплат не имеет четкой прямой взаимосвязи с размером страховых премий, что можно объяснить различием подходов к оценке и возмещению страховых случаев, а также особенностями рыночных стратегий развития и привлечения клиентов у крупнейших страховых компаний.
Таблица 11.
Аналитическая группировка крупнейших страховых компаний РФ по величине полученных страховых премий за 2012 год
| Группы страховых компаний по величине страховых премий, млрд руб. | Число страховых компаний | Страховые выплаты, млрд руб. | Количество заключенных договоров, млн шт. | ||
| всего | в среднем на 1 страховую компанию | всего | в среднем на 1 страховую компанию | ||
| 4,6–27,6 | 23 | 111,8 | 4,9 | 43,66 | 1,90 |
| 27,6–50,6 | 3 | 51,4 | 17,1 | 12,53 | 4,18 |
| 50,6–73,6 | 2 | 72,1 | 36,1 | 13,25 | 6,63 |
| 73,6–96,6 | 2 | 71,0 | 35,5 | 27,87 | 13,94 |
| Итого | 30 | 306,3 | 10,2 | 97,31 | 3,20 |
Вопрос 2. Ряды распределения.
Ряд распределения представляет собой простейшую группировку, в которой каждая выделенная группа характеризуется только количеством входящих в нее единиц совокупности. В рассмотренном нами примере с группировкой страховых организаций по величине страховых премий мы также получили ряд распределения – он записан в графах А и 1 таблицы 11.
Различают атрибутивные и вариационные ряды распределения (рис. 13).
Рис. 13. Виды рядов распределения
Атрибутивными называют ряды распределения, построенные по качественным признакам.
Вариационными называют ряды распределения, построенные по количественному признаку. Вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами называются отдельные значения признака. Варианты признака обозначаются как Хi. Частотами называются численности отдельных вариант или каждой группы вариационного ряда. Частоты показывают, как часто встречаются те или иные значения признака в изучаемой совокупности и обозначаются через fi. Сумма всех частот определяет объем совокупности. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %.
Дискретный вариационный ряд характеризуют распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, группы студентов по баллу в сессию (табл. 12).
таблица 12.
Распределение студентов по баллам в сессию (данные условные)
| Балл (оценка) | Количество студентов | Удельный вес студентов, % |
| 5 | 34 | 29,82 |
| 4 | 37 | 32,46 |
| 3 | 33 | 28,95 |
| 2 | 10 | 8,77 |
| Итого | 114 | 100,00 |
Интервальный вариационный ряд распределения – это ряд распределения, в котором группировочный признак задан интервалами значений. Например, распределение консалтинговых фирм по величине прибыли (табл. 13).
Таблица 13.
Ряд распределение консалтинговых фирм по величине прибыли за 2012 г. (данные условные)
| Прибыль, млн. руб. | Количество фирм |
| 20–40 | 5 |
| 40–60 | 15 |
| 60–80 | 20 |
| 80–100 | 10 |
Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строятполигон или гистограмму.
Полигон используется для изображения дискретных вариационных рядов. По оси абсцисс (Х) в одинаковом масштабе откладываются значения признака, а по оси ординат (Y) – частоты. Полученные на пересечении осей X и Y точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном распределения (рис. 14).
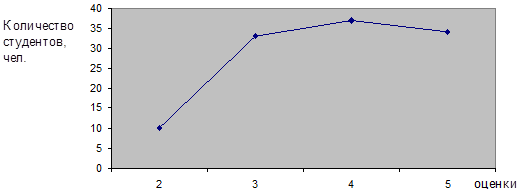
Рис. 14. Полигон распределения студентов по баллам в сессию (см. табл. 12)
Гистограмма распределения применяется для изображения интервального вариационного ряда. При ее построении на оси Х откладываются величины интервалов, а на оси Y – частоты, которые изображаются прямоугольниками, построенными на соответствующих интервалах. Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями (рис. 15).
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси Y наносят не частоты, а плотность распределения признака в соответствующих интервалах. Плотность распределения – это частота, рассчитанная на единицу ширины интервала.
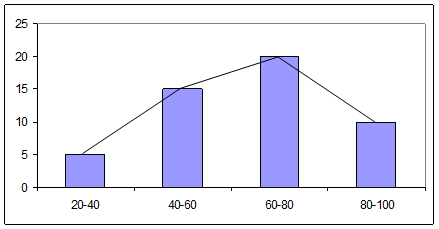
Рис. 15. Гистограмма и полигон распределения консалтинговых фирм по величине прибыли за 2012 г. (см. табл. 13)
Вопросы для самопроверки:
1. В чем заключается основная задача метода группировки?
2. Какие виды группировок применяются?
3. Что такое ряд распределения и чем он отличается от группировки?
4. Как можно определить число групп при группировке данных?
5. Может ли качественный признак являться основанием группировки?
6. В чем отличие ряда распределения от статистической групировки?
7. Можно ли построить гистограмму по данным о распределении семей по числу детей?
Литература по теме:
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Практические задания:
Задание 1.
Вы начали кампанию по улучшению качества продукции на вашей бумажной фабрике и для этих целей собрали большое количество докладных записок о проблемах потребителей. Представленная в каждой докладной записке проблема кодируется следующим образом: А – отсутствие бумаги; Б – бумага слишком толстая; С – бумага слишком тонкая; D – ширина бумаги не соответствует стандарту; E – не тот цвет бумаги; F – края бумаги крупно обрезаны. Собранная информация приведена ниже:
А, А, E, A, A, A, B, A, A, A, B, A, B, F, F, A, A, A, A, A, B, A, A, A, C, D, F, A, A, E, A, C, A, A, A, F, F, D.
Обобщите этот набор данных, вычислив (с точностью до 0,01) процент проблем каждого вида в общем количестве проблем.
Задание 2.
По данным о ходе приватизации жилых помещений в РФ (табл. 14) постройте группировку областей Центрального федерального округа по % приватизированных жилых помещений от общего числа жилых помещений, подлежащих приватизации. Выделите три группы областей с равными по ширине интервалами. При помощи структурной группировки по каждой выделенной вами группе областей определите (с точностью до 0,01), долю (в %) приватизированных в 2011 году жилых помещений в целом по группе от общего числа приватизированных в 2011 году жилых помещений Центрального федерального округа. Результаты оформите в итоговой таблице 15, дав таблице название.
Таблица 14.
Приватизация жилых помещений в РФ по состоянию на 01 января 2012 г.
| | Приватизировано жилых помещений в 2011 г., тыс. ед. | Приватизировано жилых помещений с начала приватизации на 1 января 2012 г. | |
| Всего, тыс. ед. | в % от общего числа жилых помещений, подлежащих приватизации | ||
| Российская Федерация | 340,1 | 28897,4 | 75,8 |
| Центральный федеральный округ | 98,2 | 7962,1 | 73,5 |
| Белгородская область | 2,3 | 235,2 | 86,6 |
| Тверская область | 4,6 | 346,3 | 81,0 |
| Брянская область | 2,8 | 224,0 | 80,1 |
| Рязанская область | 2,4 | 254,4 | 80,1 |
| Орловская область | 1,9 | 138,6 | 79,4 |
| Ярославская область | 4,0 | 346,6 | 79,2 |
| Липецкая область | 2,0 | 213,9 | 77,6 |
| Воронежская область | 7,5 | 366,1 | 76,7 |
| Владимирская область | 4,1 | 371,2 | 76,0 |
| Ивановская область | 2,6 | 257,9 | 75,7 |
| Тамбовская область | 1,7 | 175,9 | 75,6 |
| Калужская область | 3,0 | 243,3 | 75,5 |
| Костромская область | 2,2 | 166,5 | 73,6 |
| Тульская область | 4,5 | 406,1 | 73,1 |
| Смоленская область | 2,7 | 232,3 | 72,5 |
| г. Москва | 28,4 | 2284,4 | 71,9 |
| Московская область | 19,6 | 1523,7 | 67,9 |
| Курская область | 2,1 | 175,6 | 65,3 |
