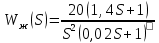Инерционное звено с ООС



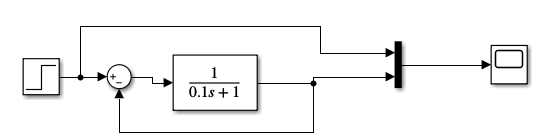
Рисунок 18 – Модель инерционного звена с ООС для переходной характеристики



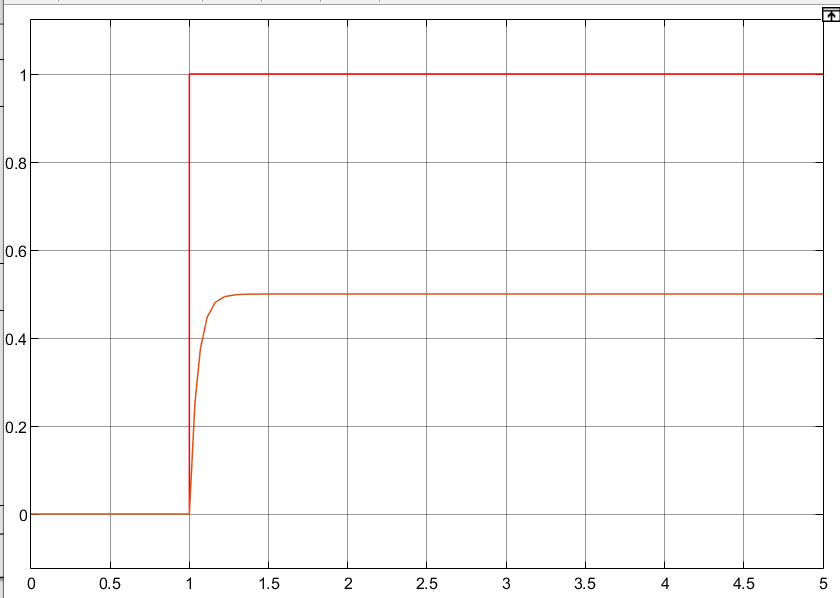
Рисунок 19 – Переходная характеристика h(t)



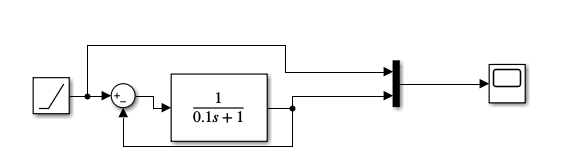
Рисунок 20 – Модель инерционного звена с ООС для реакции на линейно меняющееся воздействие



Рисунок 21 – Реакция на линейно меняющееся воздействие l(t)

6. Исследование нескорректированной замкнутой системы.

K=18



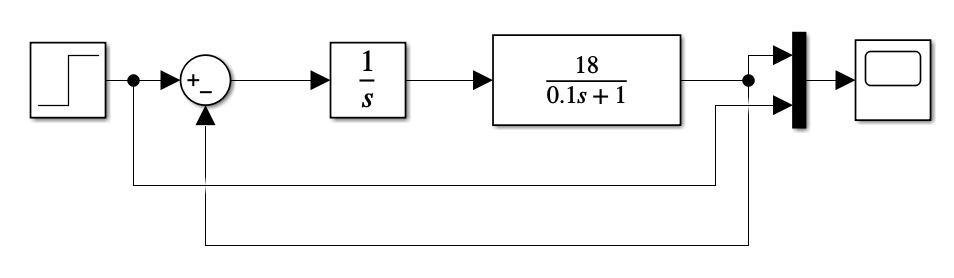
Рисунок 22

Переходная характеристика K=18



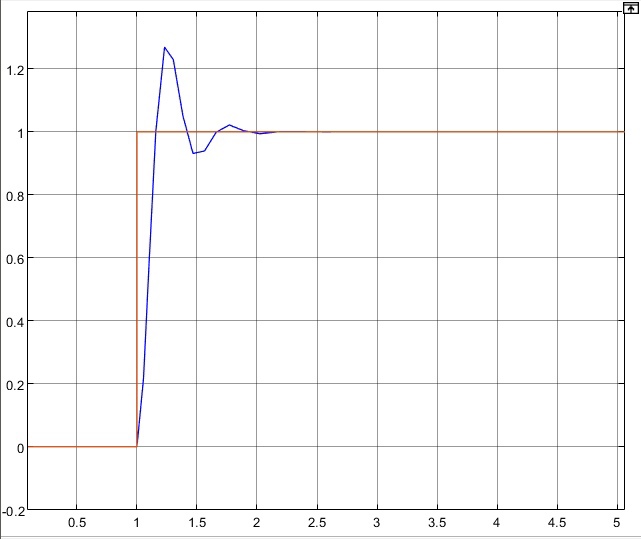
Рисунок 23

K=0.05



Рисунок 24

Переходная характеристика K=0.05



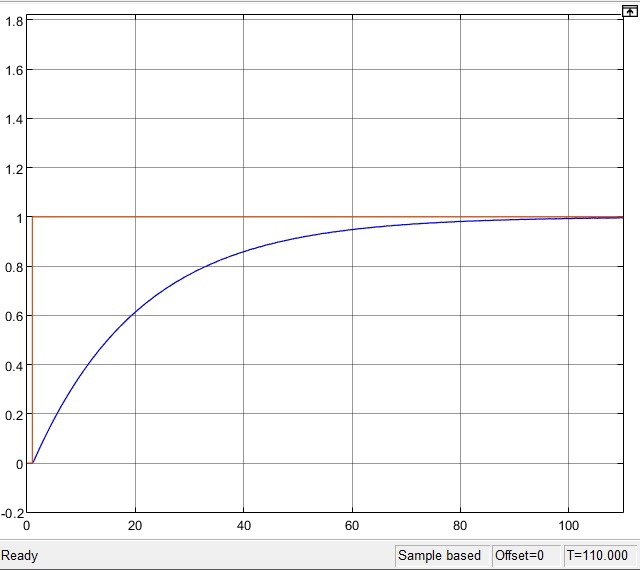
Рисунок 25

К=1



Рисунок 26

Переходная характеристика К=1



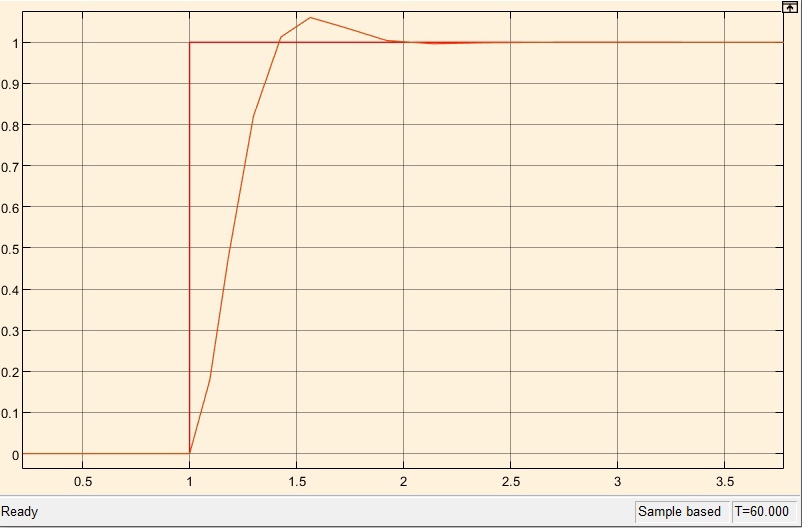
Рисунок 27

K	1	0.05	18
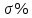	6	0	24.5
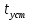	11.55	100	1.77

Кф=5,5

7. Определяем минимально допустимую величину порядка астатизма системы относительно задающего воздействие и её коэффициента усиления, а также частоту среза, обеспечивающее заданные показатели качества:

---

Определяем качество интегрирующих звеньев – порядок астатизма:

X_в

Параметры желаемой системы:





=

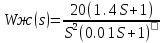
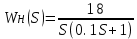
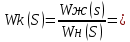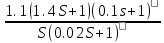
Значения ошибок:

Xмв1(t)=0.04B; Xмв2(t)=2град; Кд=0,5В/град.

Хмв1(S)=0.04/S; Xмв2=2/s

1.



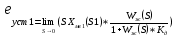
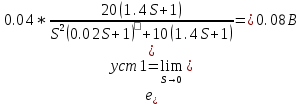
2.

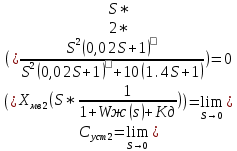
Суммарная ошибка











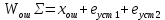
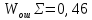
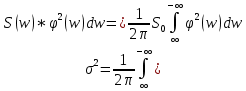
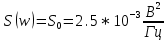
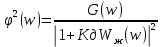
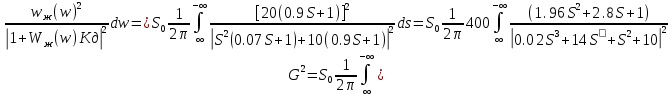ds

;





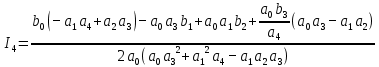
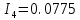
400*





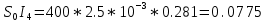
8. Исследование переходной характеристики системы при ступенчатом задающем воздействии:

1. 
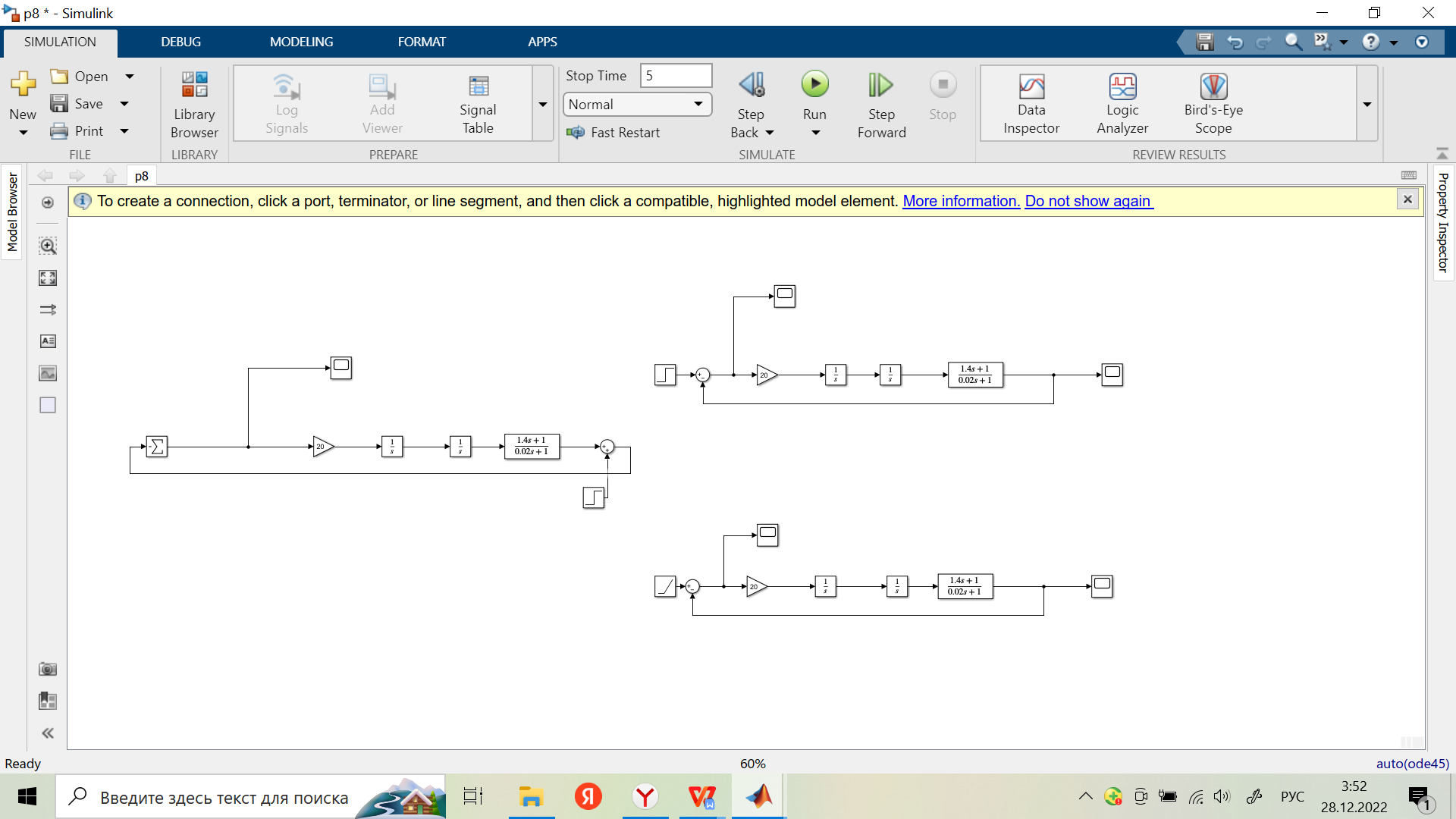
   Скорректированная замкнутая система на ступенчатое воздействие:
   

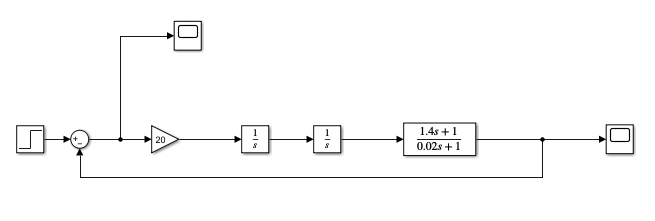
Переходная характеристика:


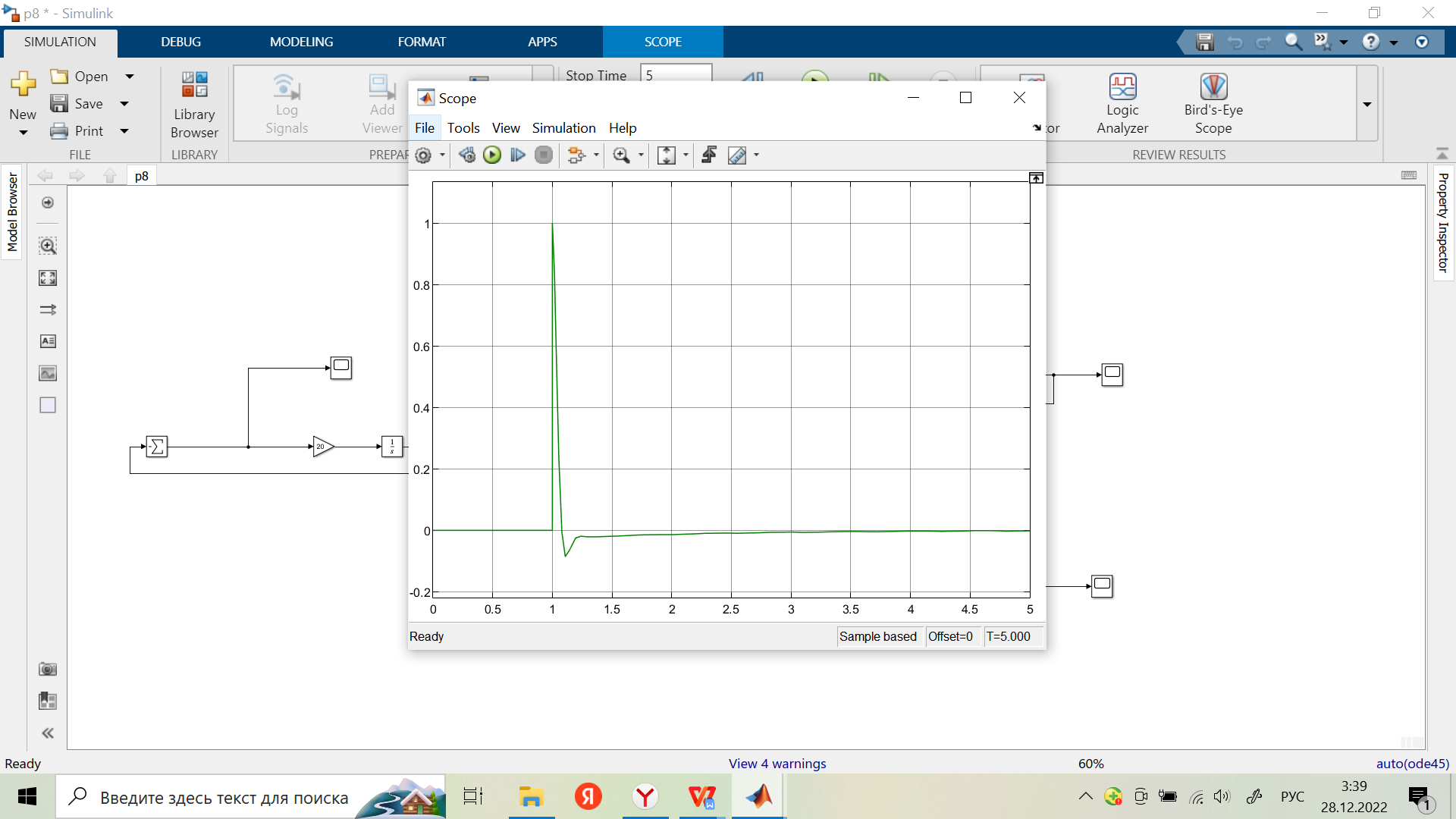
Оценивание значения установившейся ошибки и получения переходной характеристики при реакции скорректированной системы на ступенчатое воздействие:

2. 
   Скорректированная замкнутая система на линейно меняющееся воздействие:
   

---

Переходная характеристика:


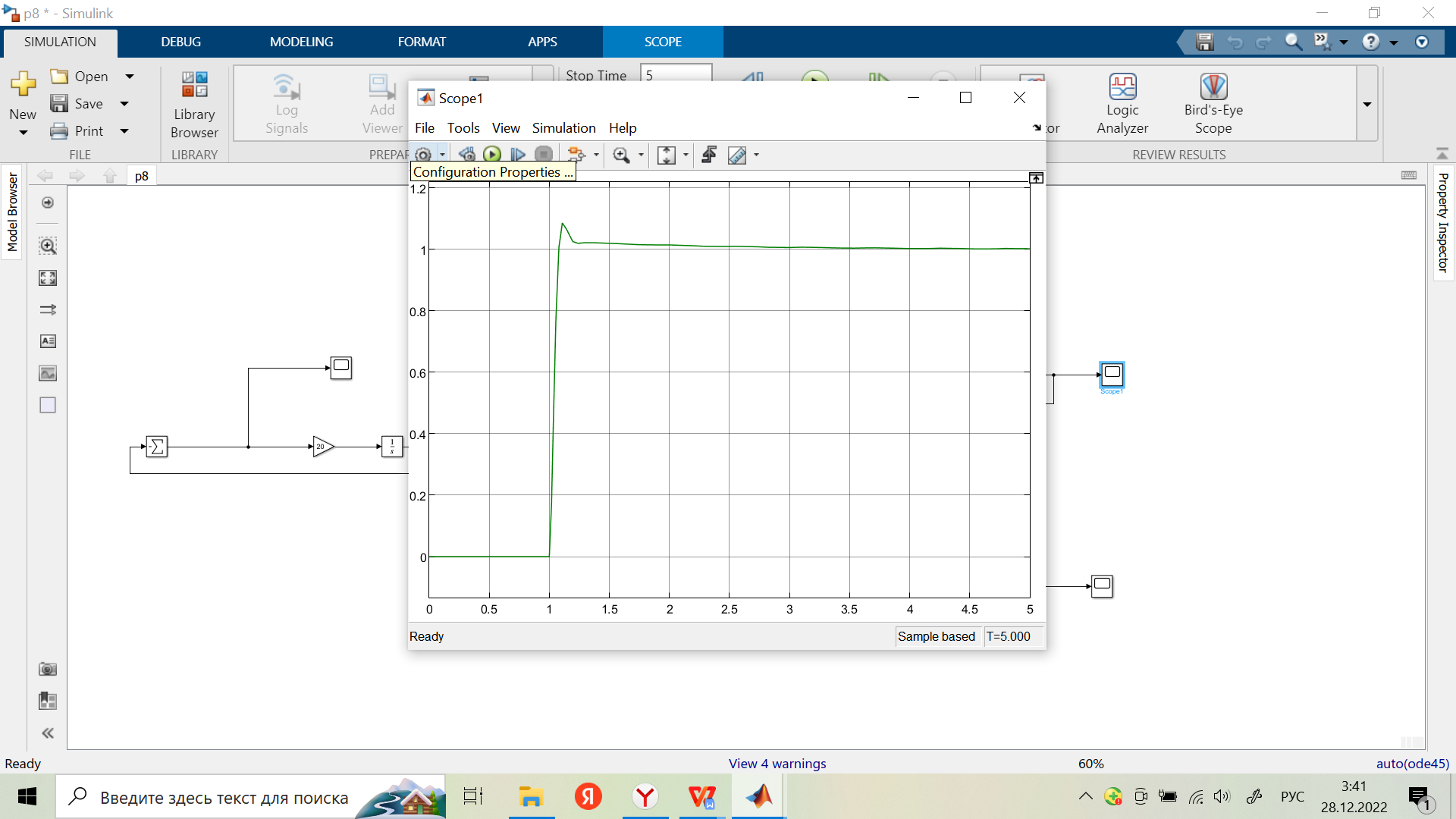
Оценивание значения установившейся ошибки и получения переходной характеристики при реакции скорректированной системы на линейно меняющееся воздействие:

3. 
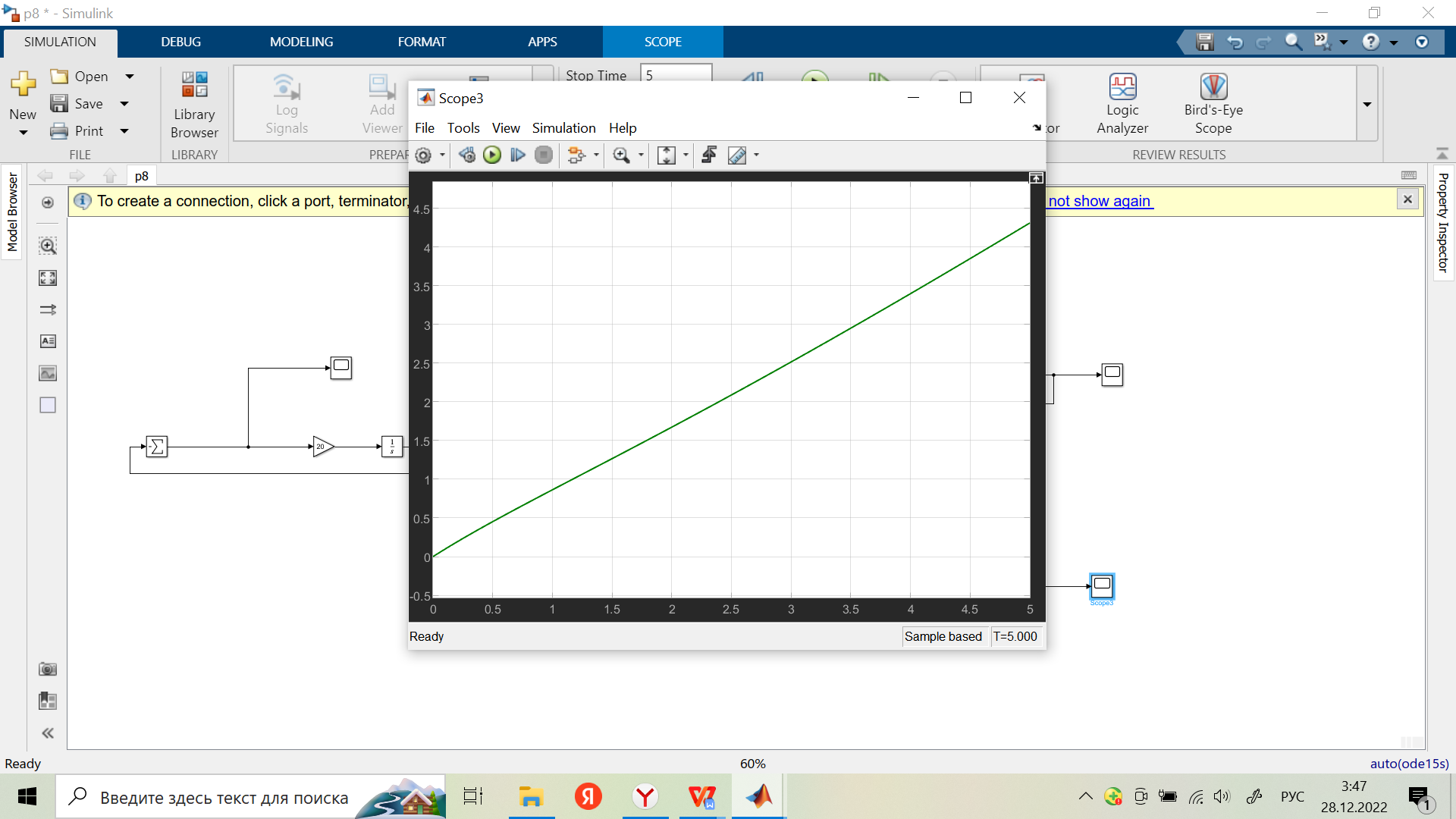
   Скорректированная замкнутая система на ступенчатое воздействие при Хмв2(t), при Хвх.в(t)=0:
   

Переходная характеристика:

4. 
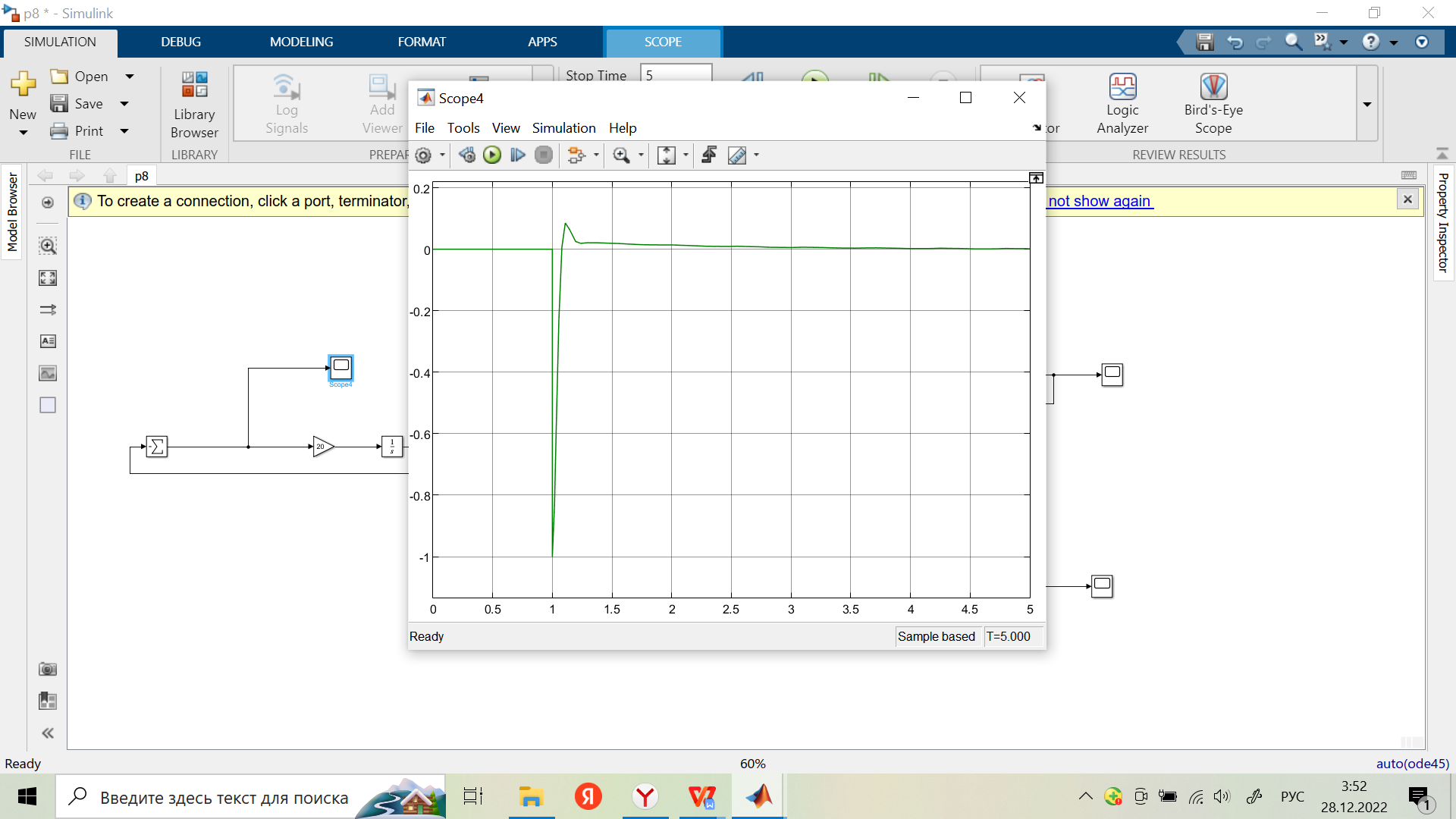
   Скорректированная замкнутая система на линейно меняющееся воздействие при Хмв2(t), при Хвх.в(t)=0:
   

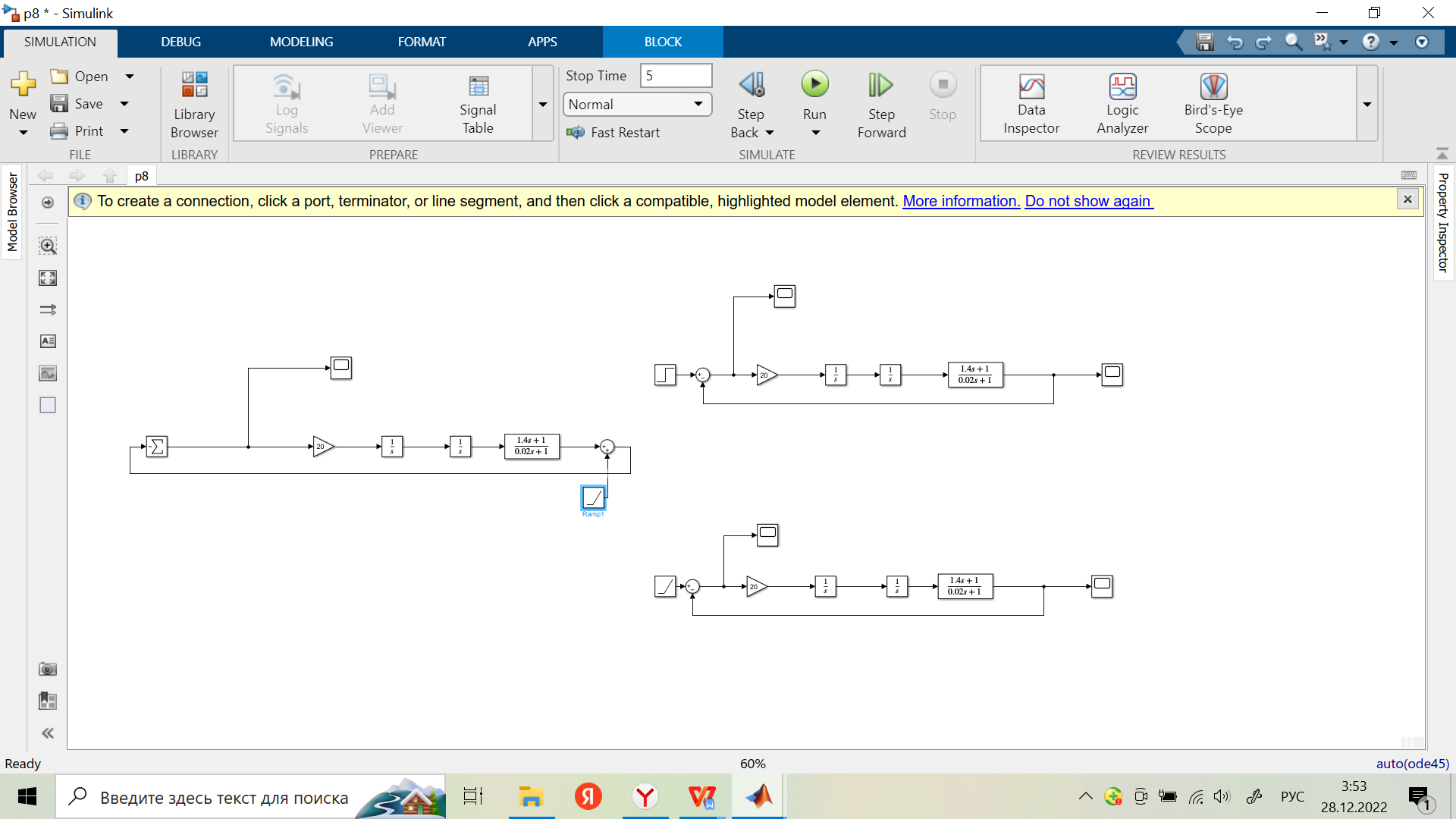
Переходная характеристика:


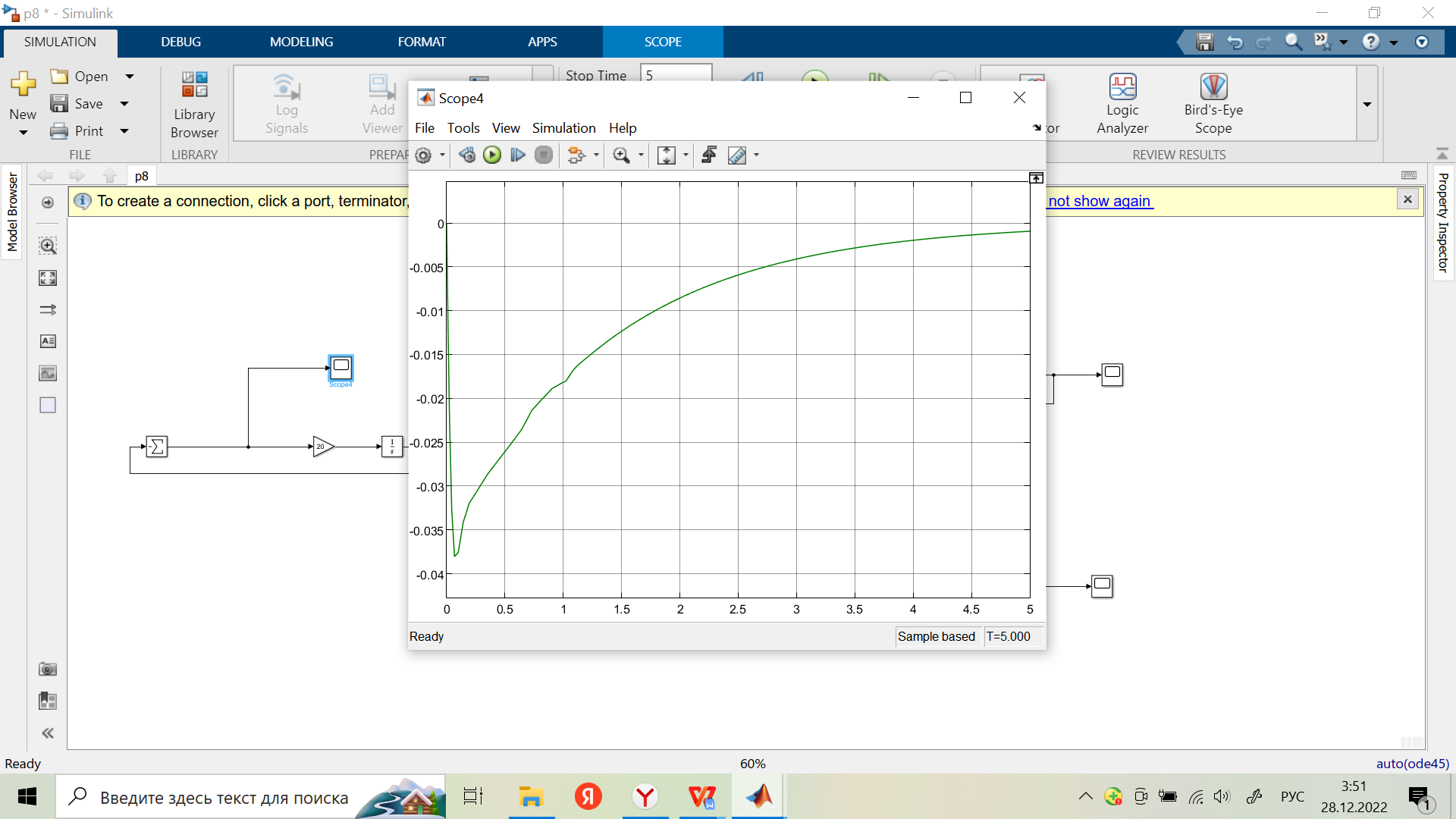
9. Рассмотрим скорректированную систему по варианту после включения в нее нелинейного звена как непрерывную и нелинейную:

Звено НЗ1:


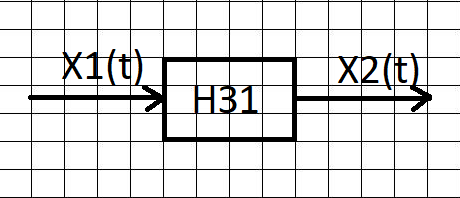
Рисунок 41


Представление звена НЗ1, как сумма простых звеньев:


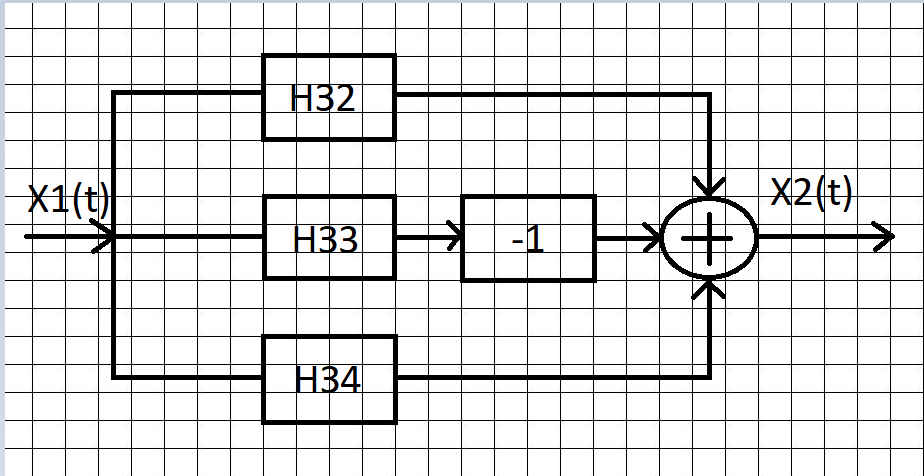
Рисунок 42
Статистические характеристики звеньев:



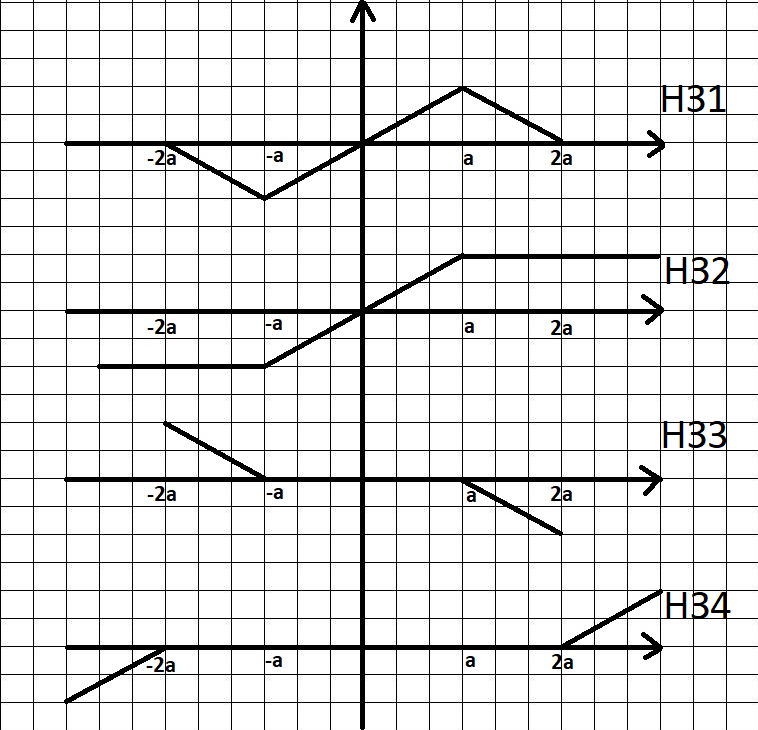
Рисунок 42




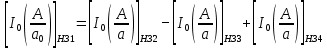
где







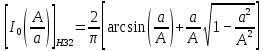
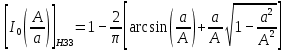
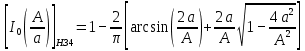
Таким образом,

---

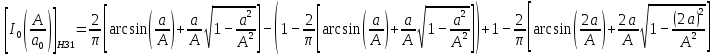
Следовательно,



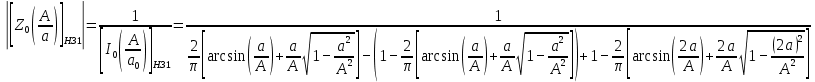
Построение зависимостей эквивалентных нормированных коэффициентов передачи от A/a.

Зависимость для первого звена – НЗ1:


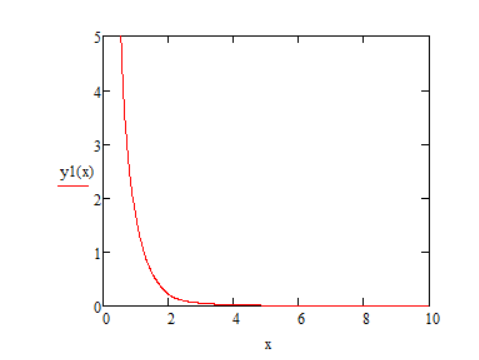
Рисунок 43
Зависимость коэффициента передачи первого звена – :


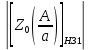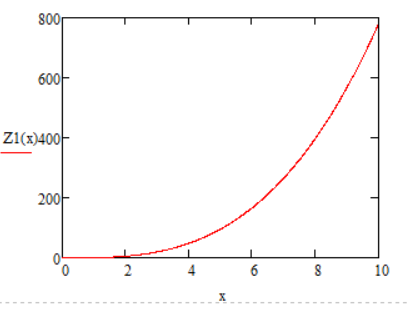
Рисунок 44

Зависимость логарифма коэффициента передачи первого звена – :


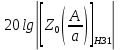Рисунок 45

Зависимость для второго звена – НЗ2: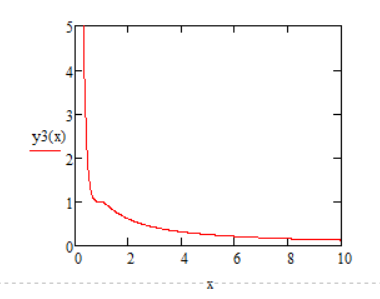


Рисунок 46
Зависимость коэффициента передачи второго звена – :


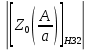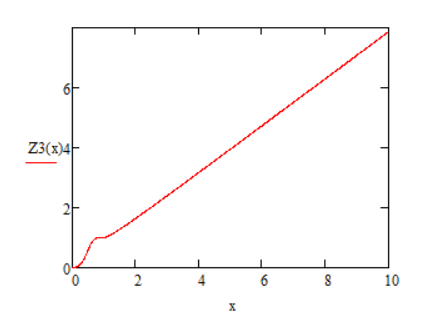
Рисунок 47

Зависимость логарифма коэффициента передачи второго звена – :


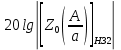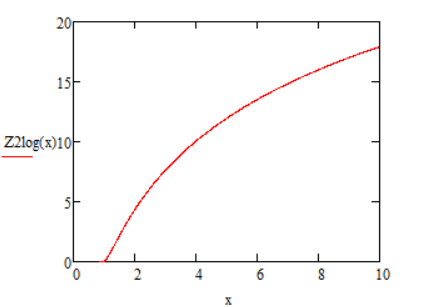
Рисунок 48

Рассчитываем для системы с S-образной треугольной характеристикой предельные значения задающего воздействия.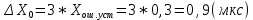







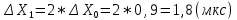
10. Исследуем на лабораторной установке режим срыва слежения в замкнутой нелинейной системе по варианту и:

Схема собранной нелинейности и осцилограмма при подаче на нелинейность линйено возрастающиего воздействия:

Рисунок 49

---

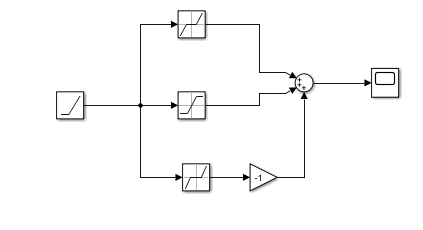
Осциллограмма при подаче на нелинейность линейно возрастающего воздействия:



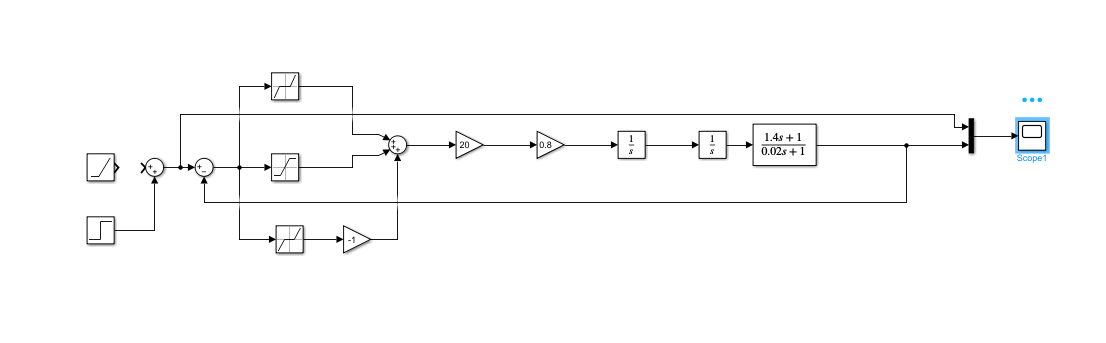
Схема замкнутой системы с нелинейной частью при ступенчатом воздействии:




Осциллограмма без изменения уровня ступенчатого воздействия:



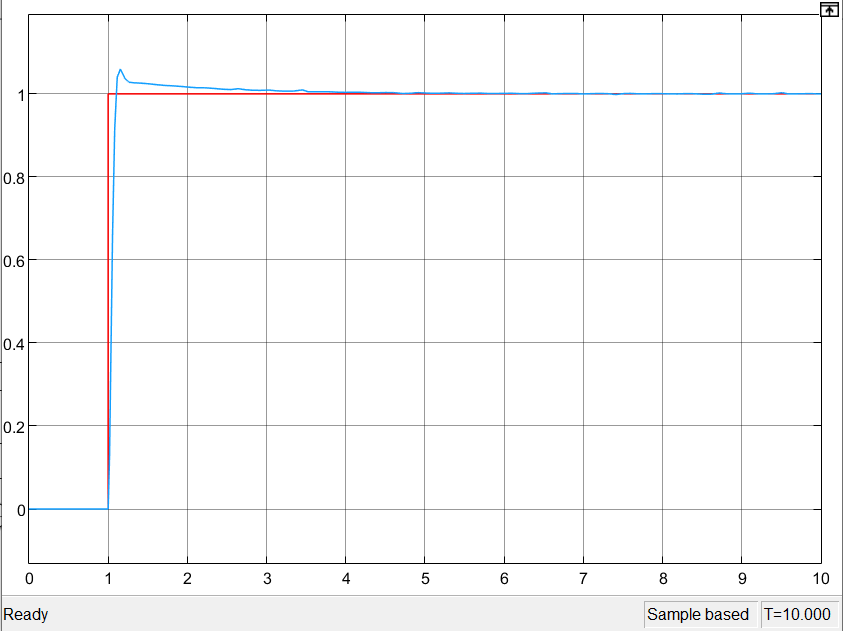
Осциллограмма при срыве слежения при амплитуде блока Slop =10:



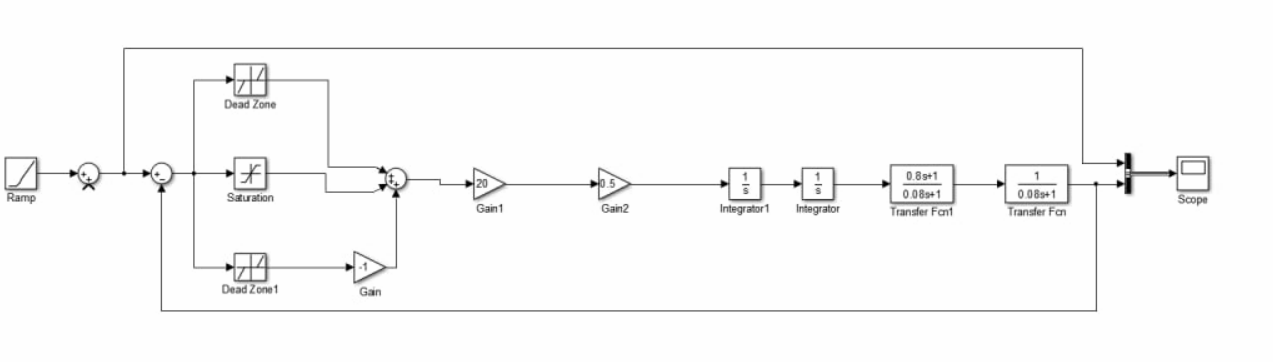
Схема замкнутой системы с нелинейной частью при линейном воздействии:

Осциллограмма без изменения угла наклона линейного воздействия:


О 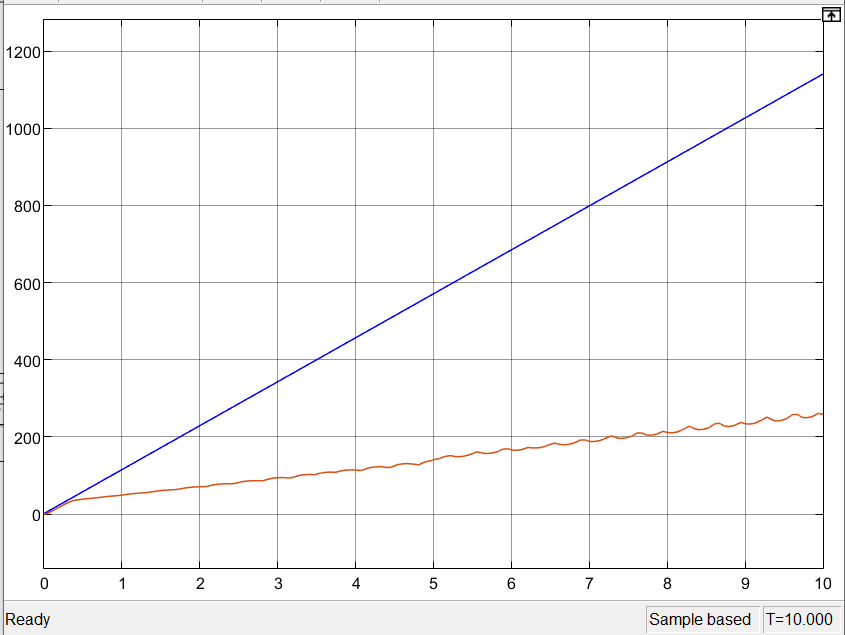осциллограмма при срыве слежения угол наклона линейного воздействия Final Value =114:

Схема замкнутой системы с нелинейной частью при сумме ступенчатого и линейного воздействия:


Осциллограмма при параметрах Slope=70 и Final Value=5:


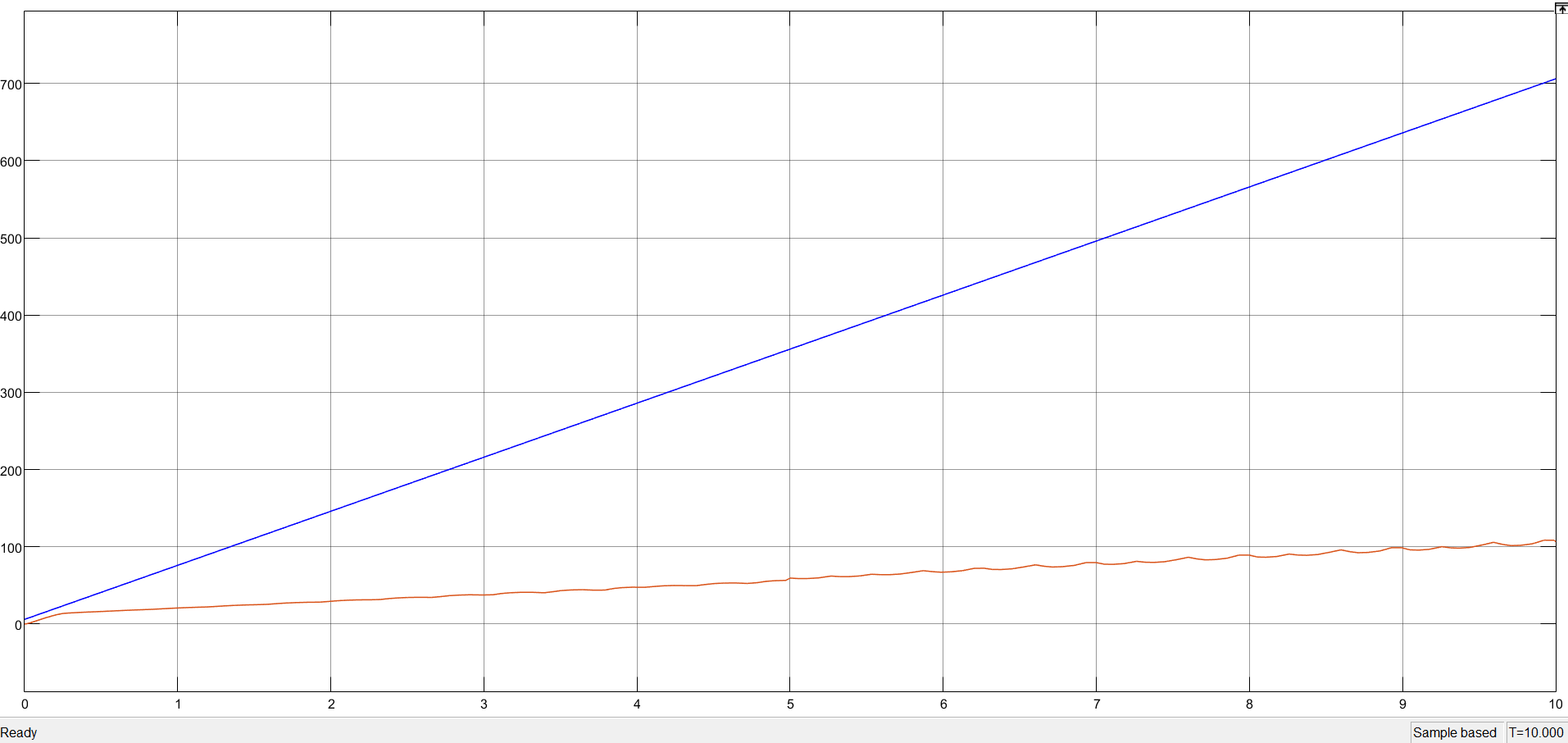
11. Составим импульсную систему, путем добавления к скорректированной системе импульсного П-образного элемента:


Непрерывная часть системы:


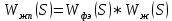
Передаточная функция формирующего элемента:


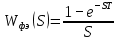
Передаточная функция желаемой системы:

---

Смотрите также файлы

• Высший медикостоматологический.docx

• Гештальттерапия Что такое гештальттерапия и как именно она помогает жить не в фантазиях, прошлом или будущем, а здесь и сейчас.docx

• Электронного документооборота.docx

• Этика науки и ответственность ученого.docx

• Эссе по самоанализу выбора будущей профессии.docx