ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Математики, физики и информационных технологий
| (наименование института полностью) |
| Прикладная математика и информатика |
| (Наименование учебного структурного подразделения) |
| 09.03.03 Прикладная информатика |
| (код и наименование направления подготовки / специальности) |
| Цифровая трансформация бизнеса |
| (направленность (профиль) / специализация) |
Практическое задание № 1
по учебному курсу « Высшая математика »
(наименование учебного курса)
Вариант 4 (при наличии)
| Обучающегося | С.Т Гусейнов | |
| | (И.О. Фамилия) | |
| Группа | ПИбд-2105а | |
| | | |
| Преподаватель | Куприенко Елена Юрьевна | |
| | (И.О. Фамилия) | |
Тольятти 2022
Задание 1
РАЗДЕЛ № 1. ЛИНЕЙНАЯ АЛГЕБРА
Задача 1
Вариант 4
Определить собственные значения и собственные векторы матрицы третьего порядка.
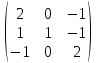
Решение. Составим и решим характеристическое уравнение.
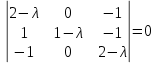
Разложим данный определитель по элементам первой строки.
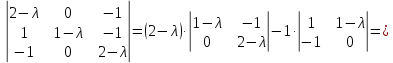
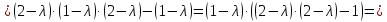
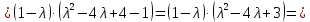
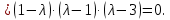Таким образом, характеристическое уравнение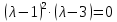
имеет двукратный корень
и простой корень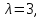 
а, следовательно, исходная матрица имеет следующие собственные числа:
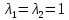и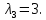 
Найдём собственные векторы, соответствующие собственному значению
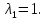
Подставляя это значение
в однородную СЛАУ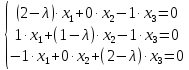
получаем однородную СЛАУ, решая которую получаем:
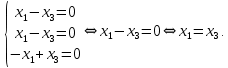
Таким образом,
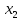и 
– свободные переменные, а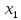 
– базисная. Построим фундаментальную систему решений.
1)
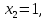
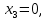откуда 
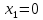и первый вектор ФСР, это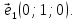 
2)
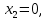
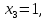откуда 
и второй вектор ФСР, это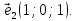 
Множество всех решений этой системы можно записать в виде: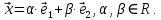
Таким образом пространство решений является двухмерным линейным пространством, один из базисов которого составляет система векторов
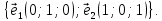Эти векторы и являются собственными векторами данной матрицы соответствующие собственному значению 
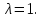Другие собственные векторы коллинеарные этим векторам.Найдём собственные векторы, соответствующие собственному числу
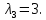
Подставляя это значение
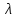в однородную СЛАУ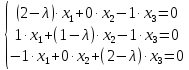 теперь получаем однородную СЛАУ, решая которую имеем:
Таким образом,
– свободная переменная, а 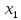и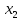 – базисные. Построим фундаментальную систему решений.
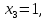откуда 
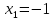и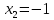 
получаем единственный вектор 
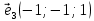ФСР. Множество всех решений этой системы можно записать в виде:
Таким образом, пространство решений является одномерным линейным пространством, один из базисов которого составляет вектор
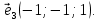Этот вектор и является собственным вектором данной матрицы соответствующие собственному значению 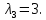Другие собственные векторы коллинеарны этому вектору.Ответ:
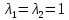и 
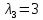– собственные значения данной матрицы, а 
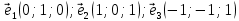– её собственные векторы.Задача 2
Вариант 4
Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.
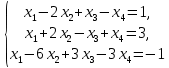
Решение. Применим теорему Кронекера- Капелле согласно которой СЛАУ совместна тогда и только тогда, когда ранг матрицы коэффициентов равен рангу расширенной матрицы. Запишем расширенную матрицу данной СЛАУ и с помощью строчных элементарных преобразований сведём её к трапециевидной форме.
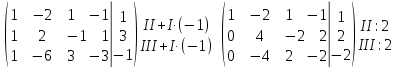
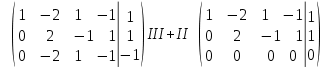
Итак, ранг матрицы коэффициентов равен 2 и равен рангу расширенной матрицы, следовательно доказано, что данная СЛАУ совместна. Так как число неизвестных равно 4, а общий ранг матицы коэффициентов и расширенной матрицы равен 2, то данная СЛАУ имеет бесконечно много решений.
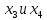– свободные переменные, 
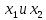базисные переменные. Запишем соответствующую СЛАУ равносильную исходной СЛАУ и выразим базисные переменные через свободные.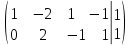
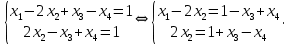
а) решим последнюю СЛАУ:
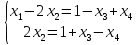методом Крамера. Имеем:Главный определитель
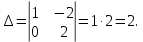
Дополнительные определители:
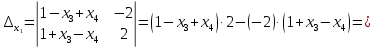
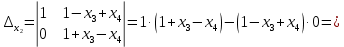
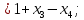
Теперь применяя формулы Крамера, получаем:
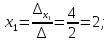
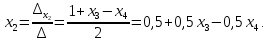
Ответ: множество решений:
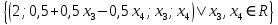
б) решим последнюю СЛАУ:
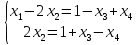методом Гаусса. Прибавим к первому уравнению – второе уравнение и разделим второе уравнение на 2.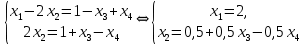
Ответ: множество решений:
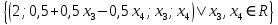
в) решим последнюю СЛАУ:
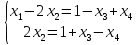средствами матричного исчисления.Рассмотрим матрицы
Тогда эту систему можно записать в матричном виде: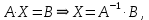
если матрица 
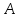имеет обратную. В данном случае определитель этой матрицы равен 
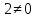и поэтому эта матрица невырожденная, а значит имеет обратную. Найдём обратную матрицу методом Гаусса. Для этого припишем к матрице
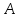единичную матрицу и с помощью строчных элементарных преобразований приведём матрицу 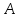к единичному виду.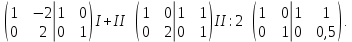
Итак,
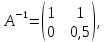откуда получаем, что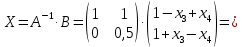 
Отсюда получаем, что
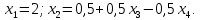
Ответ: множество решений:
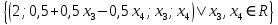
Задача 3
Вариант 4
Исследовать и найти общее решение системы линейных однородных уравнений.
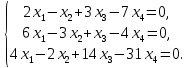
Решение. С помощью строчных элементарных преобразований сведём матрицу коэффициентов столбцы которой являются попарно различными единичными столбцами.
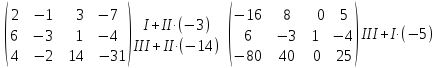
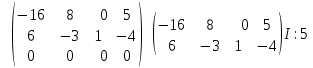
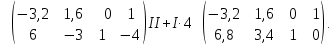
Запишем однородную СЛАУ, равносильную исходной СЛАУ, соответствующую последней матрице.
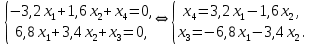
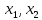– свободные переменные, 
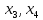– базисные. Пространство решений – двухмерное.
