Построим фундаментальную систему решений исходной однородной СЛАУ.

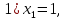
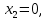откуда а Тогда первый вектор ФСР, это вектор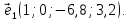

2) 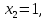откуд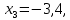а а 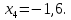Отсюда второй вектор ФСР, это вектор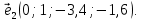

Множество всех решений этой системы можно записать в виде:

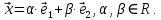
Ответ: множество решений

РАЗДЕЛ № 2. ВЕКТОРНАЯ АЛГЕБРА
Задача 1

Вариант 4

Составить уравнение плоскости , проходящей через точку 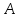перпендикулярно вектору . Написать её общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости проходящей через точки 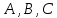. Найти угол между плоскостями и Найти расстояние от точки до плоскости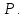



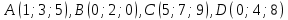
Решение. Найдём координаты вектора вычитая из координат конца соответствующие координаты его начала. Имеем:

---

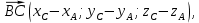
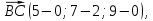
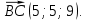
Воспользуемся уравнением плоскости по точке 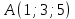и вектору нормали

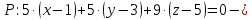уравнение плоскости по точке и вектору нормали.

Раскрыв скобки и приведя подобные, получим общее уравнение плоскости .

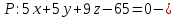общее уравнение плоскости.

Разделив обе части общего уравнения на 65, запишем уравнение плоскости в отрезках.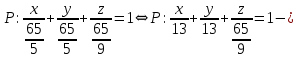

уравнение плоскости в отрезках.

Чтобы составить нормальное уравнение плоскости разделим общее уравнение этой плоскости на 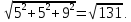Получаем: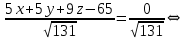



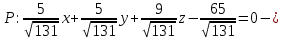нормальное уравнение плоскости .
Чтобы составить уравнение плоскости проходящей через точки воспользуемся уравнением плоскости по трём точкам:



Имеем:



Разложим последний определитель по элементам первой строки.

---

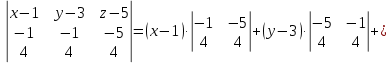
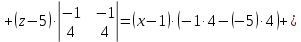
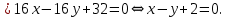
Итак, 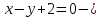общее уравнение плоскости

Угол между плоскостями и найдём как угол между их векторами нормалями и 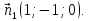Используя скалярное произведение двух векторов получаем: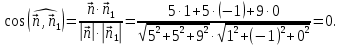


Таким образом, 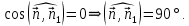Следовательно, плоскости и – перпендикулярны.

Расстояние от точки до плоскости найдём по формуле: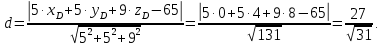



Ответ:

Задача 2

Вариант 4

Прямая задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой , проходящей через точку 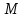параллельно прямой , и вычислить расстояние между ними. Найти проекцию точки 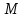на прямую и точку пересечения прямой и плоскости .



Решение. Для перехода от общего уравнения прямой к каноническому нужно найти координаты какой ни будь точки этой прямой

---

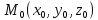
найдя какое ни будь решение системы 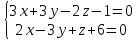и найти направляющий вектор прямой как векторное произведение векторов нормале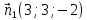й и 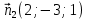заданных плоскостей: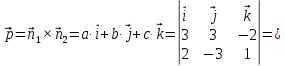





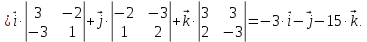
Найдём Пусть Подставляя в систему уравнений

получаем, что



Итак, отсюда получаем каноническое уравнение прямой




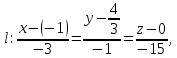
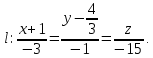
Чтобы получить параметрическое уравнение прямой , полагаем, что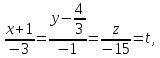



откуда получаем параметрическое уравнение прямой



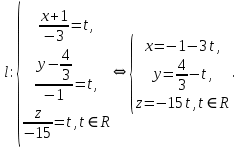
Составим уравнение прямой , проходящей через точку 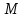параллельно прямой . Так как прямая , то направляющий вектор прямой тот же, что и у прямой : Отсюда составляем каноническое уравнение прямой

---

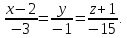
Расстояние между параллельными прямыми и найдём, учитывая геометрическое свойство векторного произведения векторов: Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на ребрах. В качестве векторов возьмём вектор 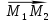и направляющий вектор (см. рис. 1).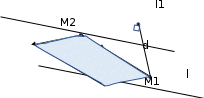


Рис.1

В данном случае










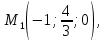
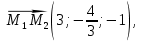
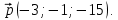
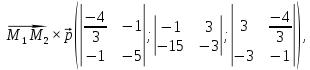
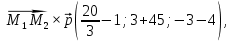
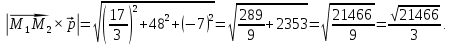
Так как площадь параллелограмма равна произведению основания на высоту, то искомое расстояние между параллельными прямыми и равно:



Найдём проекцию точки 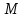на прямую . В трёхмерном пространстве проекцией точки 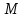на прямую будет служить точка пересечения прямой и плоскости 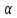, проходящей через точку

---

Смотрите также файлы

• Образование Древнерусского государства. Организация власти и управления.docx

• Курс лекций Правила оказания первой помощи.pdf

• Порядок сдачи научнотехнических отчетов.doc

• Формирующиеся ценности.docx

• има баылау жмысыны орытындылары бойынша талдау аза тілі пні бойынша Сынып.docx