ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 22
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
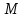и перпендикулярной прямой 
.Таким образом, направляющий вектор
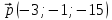прямой будет вектором нормали плоскости
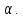Составим уравнение плоскости 
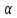по точке 
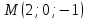и вектору нормали .
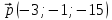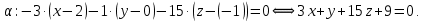
Для того, чтобы найти точку пересечения прямой
и плоскости 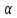воспользуемся параметрическим уравнением прямой и подставим координаты текущей точки прямой в уравнение плоскости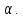 
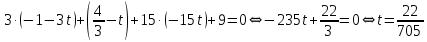
Подставляя
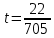в параметрическое уравнение прямой находим координаты проекции точки 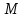на прямую .
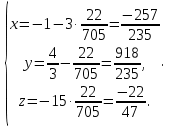
Ответ: проекцией точки
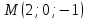на прямую является точка с координатами: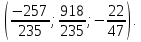
Найдём точку пересечения прямой
и плоскости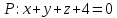 
. Для этого воспользуемся параметрическим уравнением прямой и подставим координаты текущей точки прямой
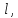в уравнение плоскости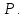 
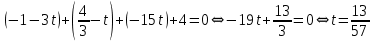
Подставляя
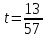в параметрическое уравнение прямой находим координаты точки пересечения прямой и плоскости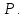 
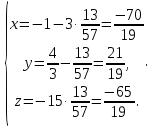
Ответ: координаты точка пересечения прямой
и плоскости 
имеет координаты: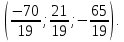 
РАЗДЕЛ № 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Задача 1
Вариант 4
Даны координаты вершин треугольника
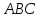. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла 
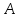, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.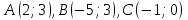
Решение. Составим уравнения сторон треугольника. Воспользуемся уравнением прямой по двум точкам.
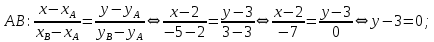
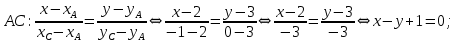
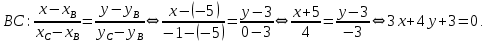
Составим уравнения медианы, высоты и биссектрисы угла
, найдём их длины. Пусть
– середина стороны 
Тогда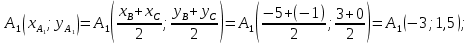 
Составим уравнение медианы
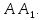
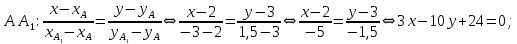
Вычислим дину медианы
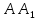
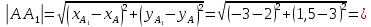
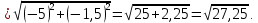
Составим уравнение высоты
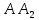.Так как направляющий вектор прямой имеет координаты
(
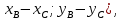то направляющий вектор высоты 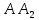будет иметь координаты (
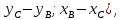поэтому имеем: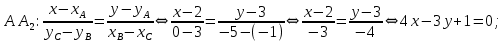
Вычислим длину высоты
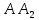для чего найдём точку 
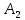– пересечения прямых 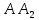и 
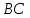. Рассмотрим систему из уравнений прямых 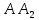и .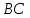
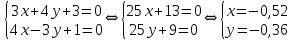
Итак,
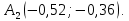Отсюда имеем: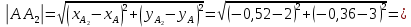
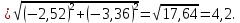
Составим уравнение биссектрисы угла
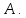В качестве направляющего вектора возьмём вектор 
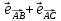, где 
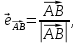а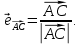 
Имеем,
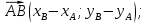
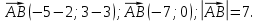
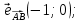
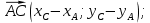
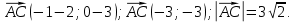
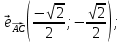
Итак,
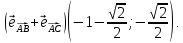Отсюда получаем уравнение биссектрисы 
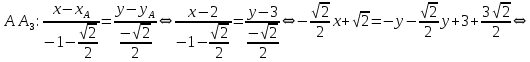
Найдём координаты точки
– пересечения биссектрисы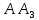 
и прямой 
.Рассмотрим систему из уравнений прямых
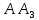и .
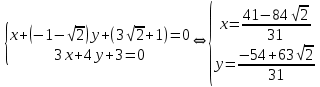
Найдём длину биссектрисы
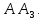
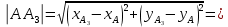
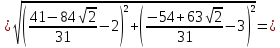
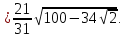
Составим уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.
Направляющими векторами данных прямых являются
, 
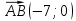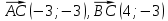.Прямая проходящая через точку
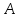параллельно стороне :
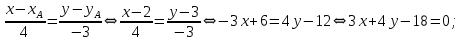
Прямая проходящая через точку
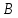параллельно стороне 
:
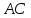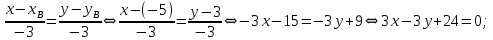
Прямая проходящая через точку
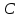параллельно стороне 
:
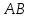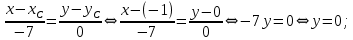
Задача 2
Вариант 4
По координатам вершин пирамиды
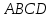
средствами векторной алгебры найти:
1) длины ребёр
и 
;2) угол между ребрами
и ;3) площадь грани
;4) проекцию
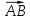на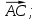 
5) объём пирамиды.
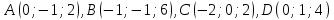
Решение.
1) найдём длины ребёр
и . Найдём координаты векторов 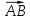и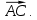 
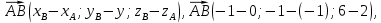
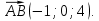
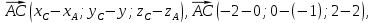
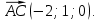
Найдём модули этих векторов.
Модуль (длина) вектора
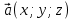выражается через его координаты формулой: 
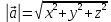. Отсюда имеем: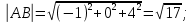
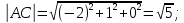2) угол α между ребрами и найдём как угол между векторам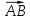и и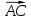 
с помощью скалярного произведения векторов.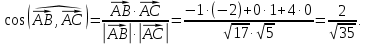
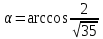. 3) площадь грани
найдём, учитывая геометрическое свойство векторного произведения векторов: модуль векторного произведения двух неколлинеарных векторов равен площади параллелограмма, построенного на этих векторах как на рёбрах.