Вариант 1
Задача 1
В базе данных магазина, торгующего подержанными автомобилями, содержится информация об их потребительский свойствах и ценах.

Для анализа зависимости цены автомобиля Y от его возраста Х₁ и мощности двигателя Х₂ из базы данных выбраны сведения о 16 автомобилях. Эти сведения приведены в таблице1.

номер	цена	возраст	мощность
1	8,3	6	88
2	17,9	3	160
3	11,2	5	105
4	17,2	4	165
5	9,4	5,5	88
6	15,9	4	145
7	6,8	7	95
8	10,8	6	124
9	15,6	5	165
10	13,8	3,5	112
11	15,3	3	120
12	14,4	4,5	145
13	15,6	3,5	140
14	10,6	7	145
15	11,2	5,5	120
16	13,4	4,5	132

1. 
   Парные зависимости
   
   1. 
      Построить поля рассеяния для цены Y и возраста автомобиля Х₁, а также для цены Y и мощности двигателя Х₂. На основе их визуального анализа выдвинуть гипотезы о виде статистической зависимости Y от Х₁ и Y от Х₂ и записать их математически.
      

---

Построим поля рассеяния:



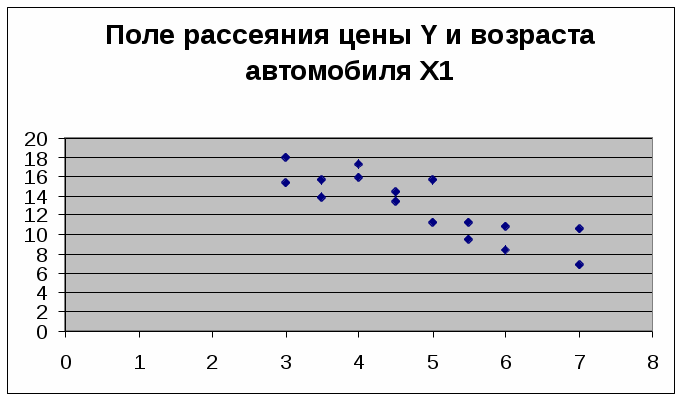
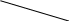
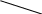
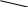
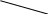
Рис. 1. Поле рассеяния для цены Y и возраста автомобиля Х₁



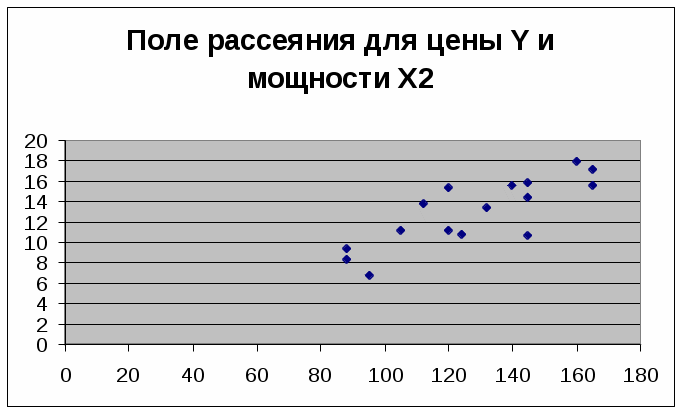
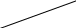
Рис. 2 Поле рассеяния для цены Y и мощности двигателя Х₂
На основе визуального анализа построенных полей рассеяния можно выдвинуть гипотезу о линейной зависимости цены от возраста Х₁ и мощности двигателя Х₂.

Математически данные зависимости запишутся в виде:

y = α₀+ α₁x₁ +

и y = β₀+ β₁x₁ + , где и - случайные переменные.
1.2. Методом наименьших квадратов найти оценки линейных уравнений регрессии:

y = α₀+ α₁x_1, y = β₀+ β₁x_1.

Составим вспомогательную таблицу для

---

= α₀+ α₁x₁: (таблица 2)

i	yi	xi1	xi12	yi xi1	yi2
1	8,3	6	36	49,8	68,89
2	17,9	3	9	53,7	320,41
3	11,2	5	25	56	125,44
4	17,2	4	16	68,8	295,84
5	9,4	5,5	30,25	51,7	88,36
6	15,9	4	16	63,6	252,81
7	6,8	7	49	47,6	46,24
8	10,8	6	36	64,8	116,64
9	15,6	5	25	78	243,36
10	13,8	3,5	12,25	48,3	190,44
11	15,3	3	9	45,9	234,09
12	14,4	4,5	20,25	64,8	207,36
13	15,6	3,5	12,25	54,6	243,36
14	10,6	7	49	74,2	112,36
15	11,2	5,5	30,25	61,6	125,44
16	13,4	4,5	20,25	60,3	179,56
Σ	207,4	77	395,5	943,7	2850,6

---

т.к. n=16, то = =12,9625

= = 4,8125

тогда


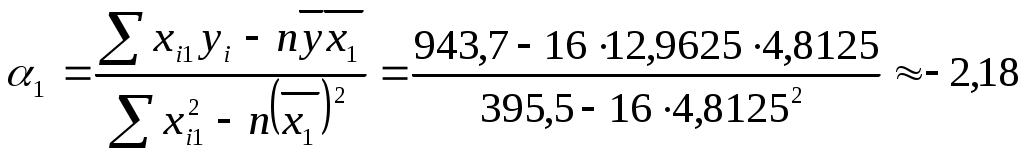
таким образом, получаем уравнение регрессии:

Составим таблицу для = β₀+ β₁x₁: (таблица 3)

i	yi	xi2	xi22	yi xi2	yi2
1	8,3	88	7744	730,4	68,89
2	17,9	160	25600	2864	320,41
3	11,2	105	11025	1176	125,44
4	17,2	165	27225	2838	295,84
5	9,4	88	7744	827,2	88,36
6	15,9	145	21025	2305,5	252,81
7	6,8	95	9025	646	46,24
8	10,8	124	15376	1339,2	116,64
9	15,6	165	27225	2574	243,36
10	13,8	112	12544	1545,6	190,44
11	15,3	120	14400	1836	234,09
12	14,4	145	21025	2088	207,36
13	15,6	140	19600	2184	243,36
14	10,6	145	21025	1537	112,36
15	11,2	120	14400	1344	125,44
16	13,4	132	17424	1768,8	179,56
сумма	207,4	2049	272407	27603,7	2850,6

---

т.к. n=16, то = =12,9625

= = 128,0625

тогда


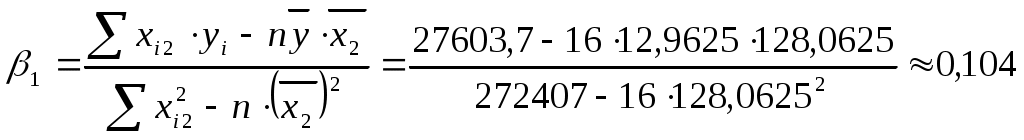
таким образом, получаем уравнение регрессии:


1.3. С помощью коэффициентов парной корреляции проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также между ценой и мощностью двигателя. Проверить их значимость с надежностью 0,9.

Найдем коэффициент парной корреляции для = α₀+ α₁x₁:



проверим, существенно ли отличается найденный коэффициент корреляции от нуля. Найдем:



Сравним с квантилем распределения Стьюдента

Т.к. 6,18489 >1,761, то коэффициент корреляции существенно отличается от нуля и существует сильная линейная зависимость между y и
Найдем коэффициент парной корреляции для = β₀+ β₁x₂:



проверим, существенно ли отличается найденный коэффициент корреляции от нуля. Найдем:



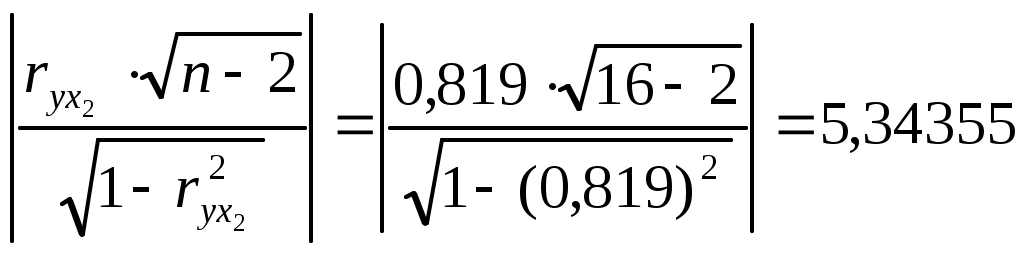
Сравним с квантилем распределения Стьюдента

Т.к. 5б34355 >1,761, то коэффициент корреляции существенно отличается от нуля и существует сильная линейная зависимость между y и

---

Смотрите также файлы

• Основные направления социальной поддержки мигрантов в рф.docx

• Лабораторная работа 8 по дисциплинам Механическое оборудование карьеров иГорные машины Автогрейдеры.docx

• Тесты по фарме.docx

• московский международный университет Кафедра.docx

• Гласные и согласные звуки и буквы. Звукобуквенный анализ и синтез слов.doc