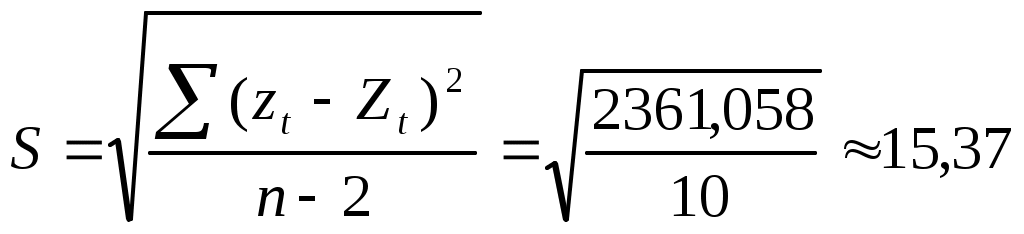, для каждого t_i рассчитаем
,

, где . Результаты расчетов для каждого приведены в таблице 10.

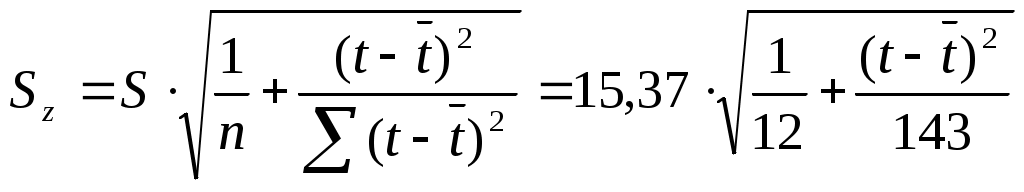Изобразим доверительную полосу (линии Zн и Zв) , линию тренда (Zt), и исходный временной ряд (z t) на графике: (рис. 4)


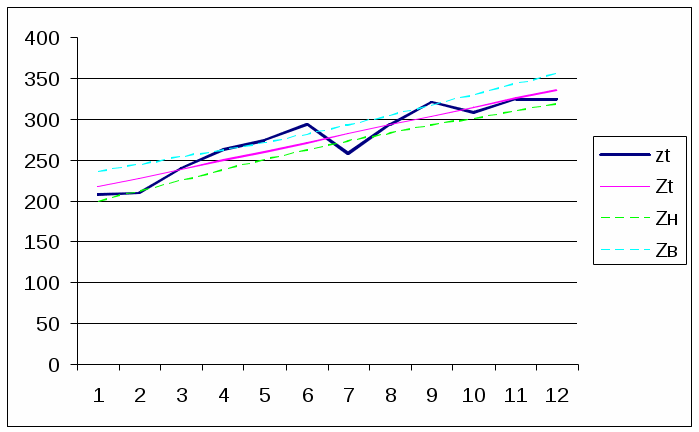
рис. 4

3. 
   С помощью уравнения тренда найти точечный и интервальный прогноз (надежности 0,95) для среднего объема продаж на конец первого квартала текущего года.
   

В данном случае t = 12+3 = 15.

Точечный прогноз:



Интервальный прогноз:

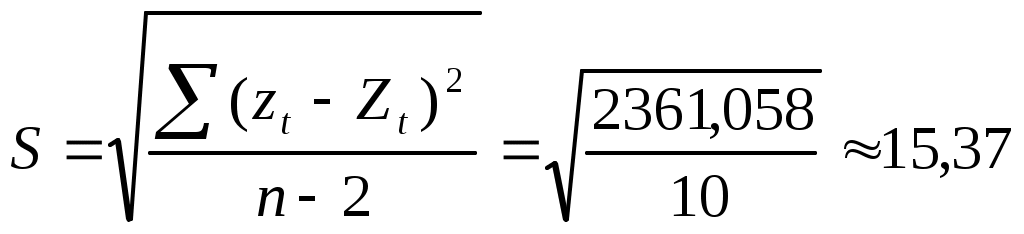, рассчитаем
,

, где . Т.е.




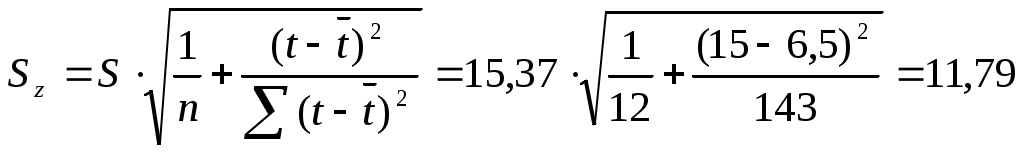Т.е. с надежностью 95% средний объем продаж на конец первого квартала текущего года попадет в интервал (341,93 ; 394,51).

Задача 3

Проверка моделей на автокорреляцию и мультиколлинеарность.

1. 
   Для регрессионных моделей
   

и с помощью критерия Дарбина – Уотсона проверить наличие или отсутствие автокорреляции на уровне значимости α = 0,01
Для :
Вычислим d-статистику Дарбина-Уотсона:

---

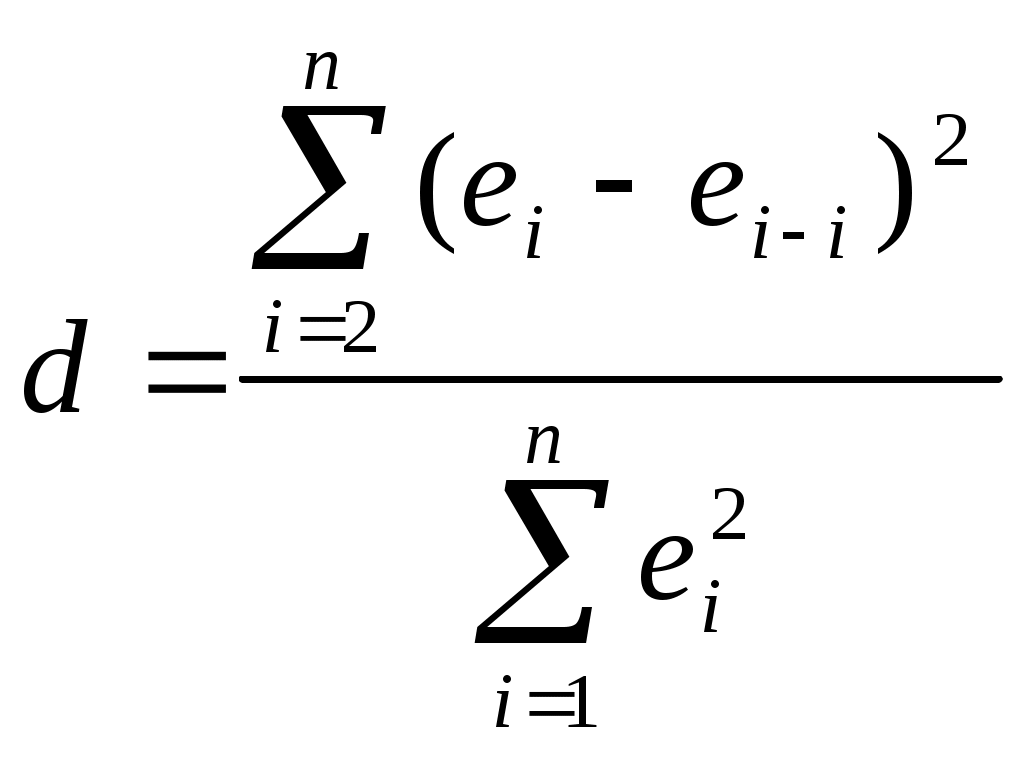
, где на основе 2 столбца таблицы 7 вычислим числитель формулы:

	(ei –ei-1)2
	0,0441
	0,1089
	0,0441
	0,000625
	0,015625
	0,6889
	0,1444
	0,1156
	0,225625
	0,021025
	0,070225
	0,0016
	0,046225
	0,001225
	0,0529
Σ	1,58

Знаменатель нами уже найден, он равен 1,63, тогда

---

Табличные критические значения для уровня значимости α = 0,01, число наблюдений 16, число независимых переменных 2, равны:

и так как , то d-статистика Дарбина – Уотсона . находится в зоне неопределенности, нельзя сделать вывод о наличии или отсутствии автокорреляции.

Для :

	(ei –ei-1)2
	96,8256
	367,1056
	173,1856
	0,0256
	66,5856
	2101,306
	583,7056
	294,4656
	617,0256
	37,9456
	117,5056
Σ	4455,68

тогда Табличные критические значения для уровня значимости α = 0,01, число наблюдений 12, число независимых переменных 1, равны:

и .Так как , то делаем вывод об отсутствии автокорреляции.

2. 
   Для регрессионной модели проверить наличие или отсутствие мультиколлинеарности, используя:
   

---

а) парный коэффициент корреляции (приближенно);

б) критерий «хи-квадрат» на уровне значимости α = 0,01.
а). Рассмотрим уравнение регрессии

вычислим значение коэффициента корреляции между объясняющими переменными х₁ и х₂:



Найдем

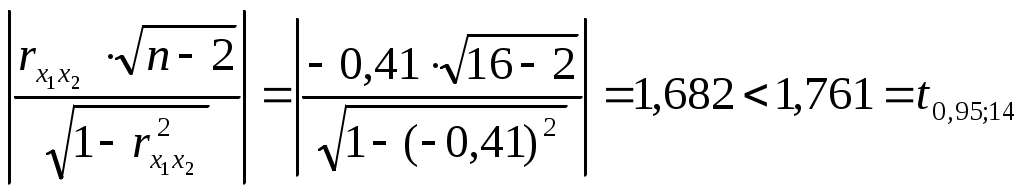, тогда коэффициент парной корреляции незначительно отличается от нуля, т.е. можно считать что переменные и не коррелируют между собой и, следовательно, нет мультиколлениарности.
б). Рассчитаем определитель матрицы коэффициентов парной корреляции:



тогда

Табличное значение статистики для df = 1 и α = 0,01 равно

Так как , то подтверждается отсутствие мультиколлинеарности.

---

Смотрите также файлы

• Основные направления социальной поддержки мигрантов в рф.docx

• Лабораторная работа 8 по дисциплинам Механическое оборудование карьеров иГорные машины Автогрейдеры.docx

• Тесты по фарме.docx

• московский международный университет Кафедра.docx

• Гласные и согласные звуки и буквы. Звукобуквенный анализ и синтез слов.doc