2. Множественная зависимость.
2.1. По методу наименьших квадратов найти оценки коэффициентов множественной линейной регрессионной модели

Составим матрицы 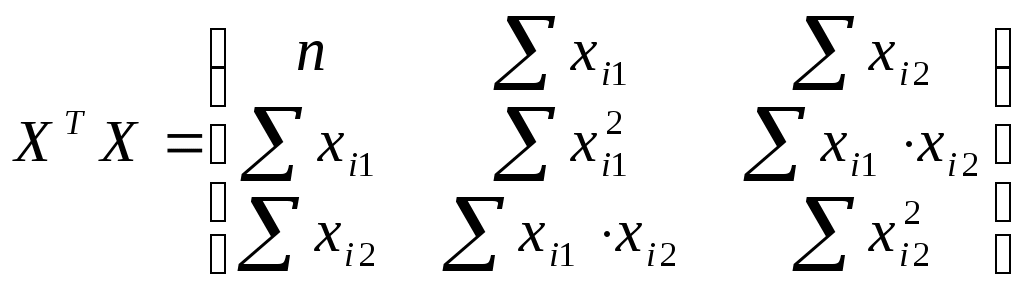и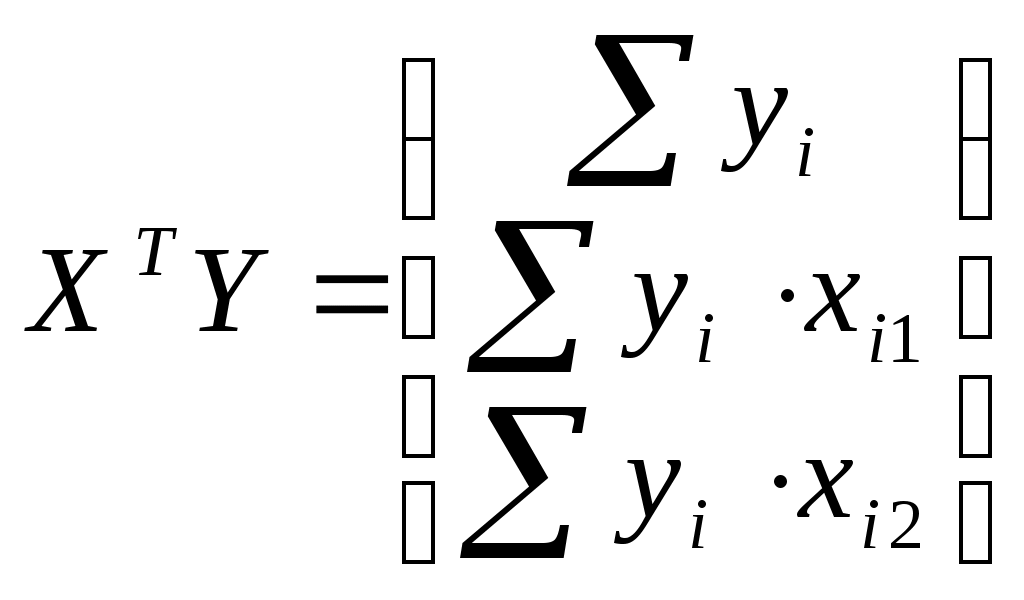

Для этого составим вспомогательную таблицу: (таблица 6)

i	yi	xi1	xi2	xi12	xi22	yi xi1	yi xi2	xi1xi2
1	8,3	6	88	36	7744	49,8	730,4	528
2	17,9	3	160	9	25600	53,7	2864	480
3	11,2	5	105	25	11025	56	1176	525
4	17,2	4	165	16	27225	68,8	2838	660
5	9,4	5,5	88	30,25	7744	51,7	827,2	484
6	15,9	4	145	16	21025	63,6	2305,5	580
7	6,8	7	95	49	9025	47,6	646	665
8	10,8	6	124	36	15376	64,8	1339,2	744
9	15,6	5	165	25	27225	78	2574	825
10	13,8	3,5	112	12,25	12544	48,3	1545,6	392
11	15,3	3	120	9	14400	45,9	1836	360
12	14,4	4,5	145	20,25	21025	64,8	2088	652,5
13	15,6	3,5	140	12,25	19600	54,6	2184	490
14	10,6	7	145	49	21025	74,2	1537	1015
15	11,2	5,5	120	30,25	14400	61,6	1344	660
16	13,4	4,5	132	20,25	17424	60,3	1768,8	594
Σ	207,4	77	2049	395,5	272407	943,7	27603,7	9654,5

---

;



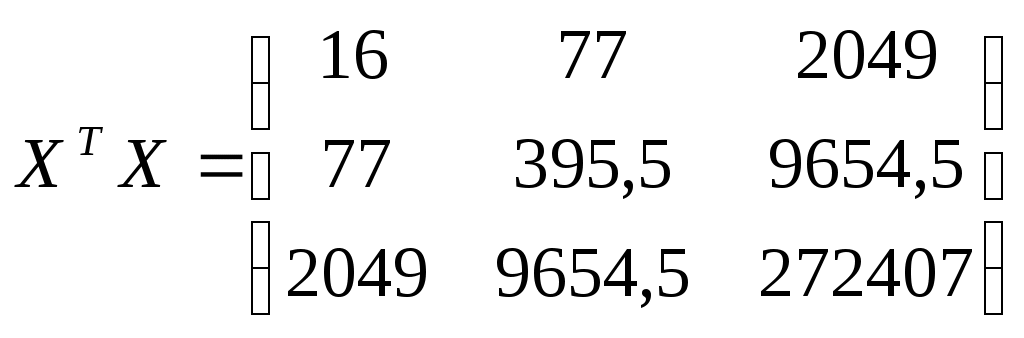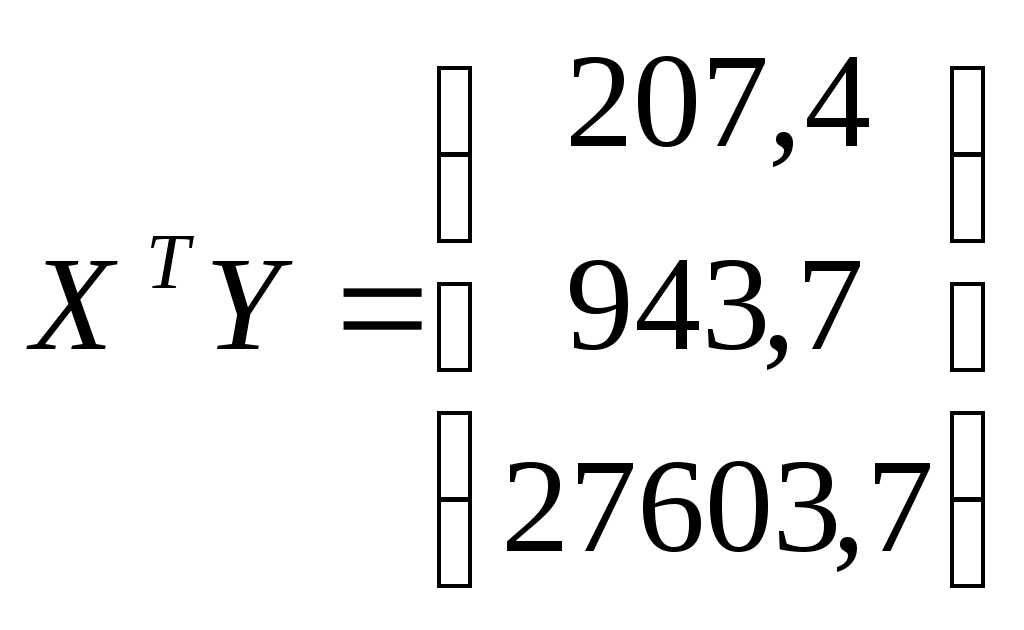
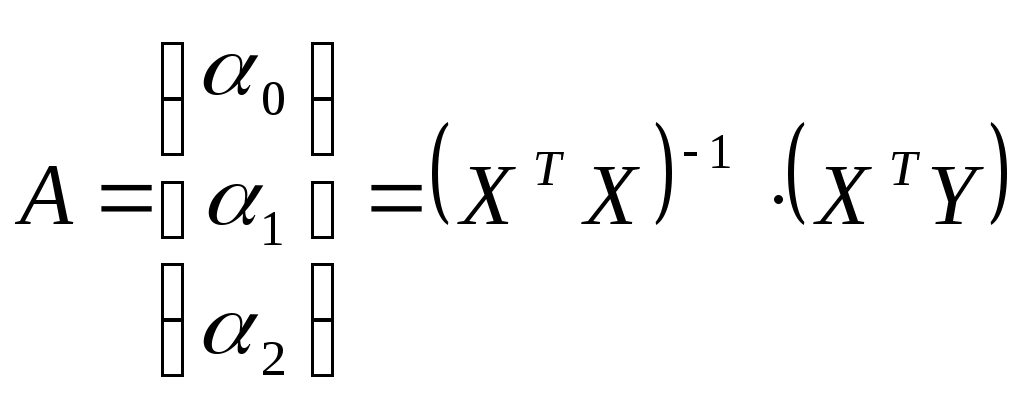
Найдем :



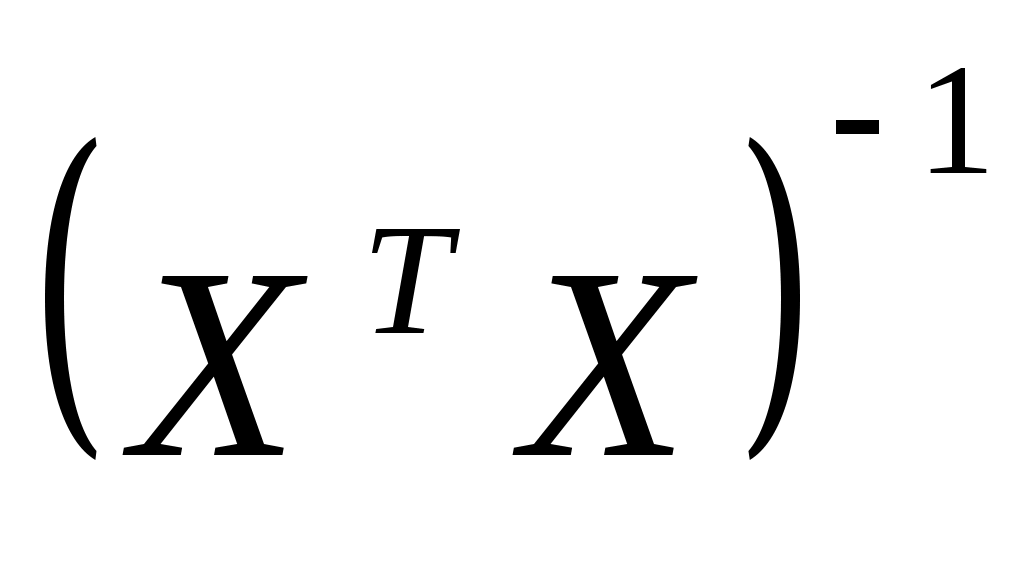алгебраические дополнения:







Тогда обратная матрица

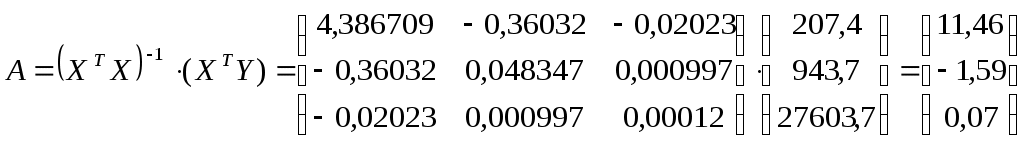таким образом, получаем уравнение регрессии:
.
2.2. Проверить статистическую значимость параметров и уравнения множественной регрессии с надежностью 0,9.
Для вычисления коэффициента детерминации составим таблицу: (таблица 7)

ỹi	ỹi -yi	(ỹi -yi )2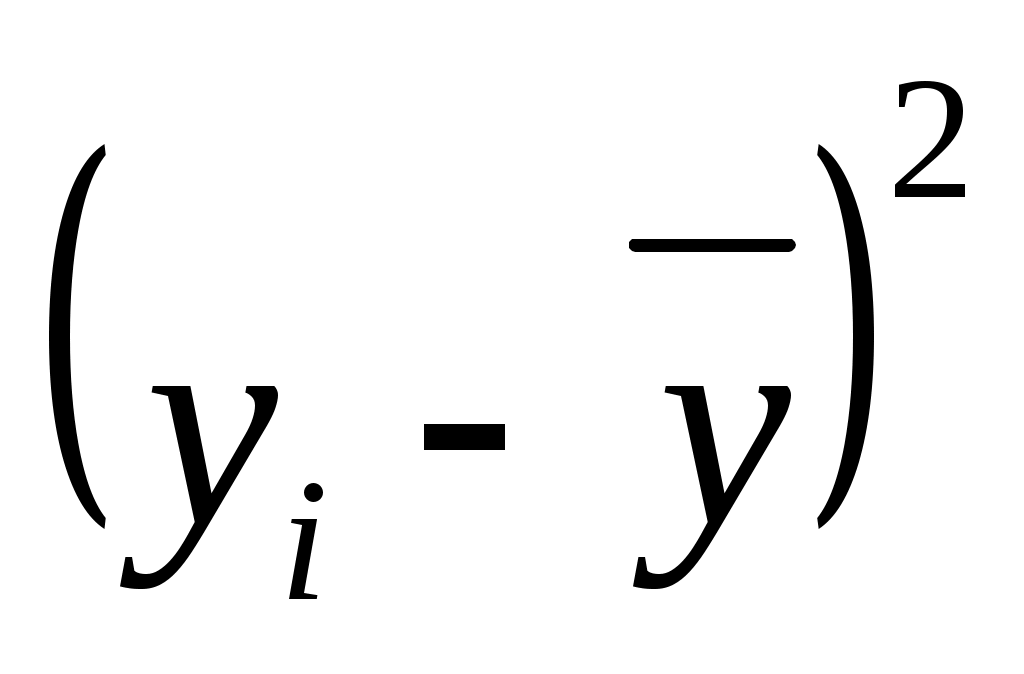
8,08	-0,22	0,0484	21,73891
17,89	-0,01	1E-04	24,37891
10,86	-0,34	0,1156	3,106406
16,65	-0,55	0,3025	17,95641
8,875	-0,525	0,275625	12,69141
15,25	-0,65	0,4225	8,628906
6,98	0,18	0,0324	37,97641
10,6	-0,2	0,04	4,676406
15,06	-0,54	0,2916	6,956406
13,735	-0,065	0,004225	0,701406
15,09	-0,21	0,0441	5,463906
14,455	0,055	0,003025	2,066406
15,695	0,095	0,009025	6,956406
10,48	-0,12	0,0144	5,581406
11,115	-0,085	0,007225	3,106406
13,545	0,145	0,021025	0,191406
		1,63	162,18

---

Коэффициент корреляции

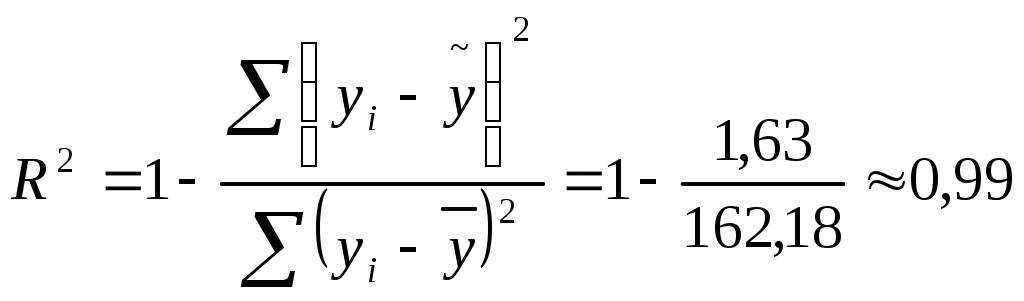
Следовательно, регрессия y на x₁ и x ₂ объясняет 99% колебаний значений у. Это свидетельствует о значительном суммарном влиянии независимых переменных x₁ и x ₂ на зависимую переменную у.

Качество уравнения множественной регрессии оценим с помощью F-теста, найдем



При уровне значимости 0,05 и табличное значение F_m=3,81. Неравенство F_mф выполняется, гипотеза о незначимости коэффициентов регрессии отклоняется и признается статистическая значимость уравнения регрессии.


2.3. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей возраста 3 года и мощностью 165 л.с. с доверительной вероятностью 0,9.
Точечный прогноз:

где - вектор независимых переменных, для которого определяется прогноз. В нашем случае

Тогда
Интервальный прогноз:

;

, где

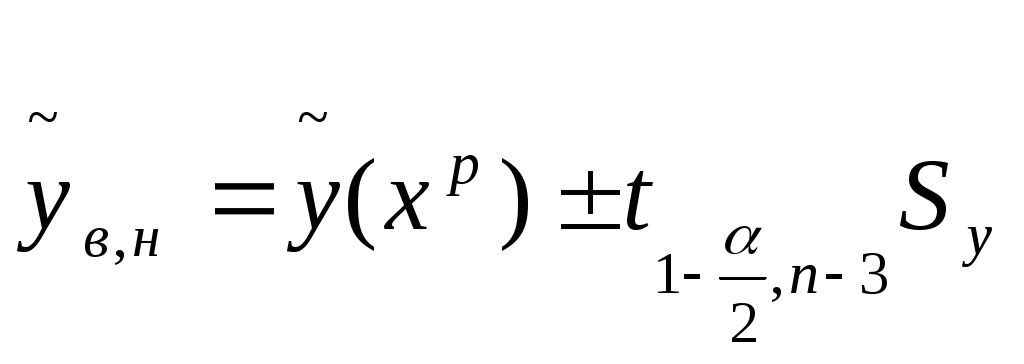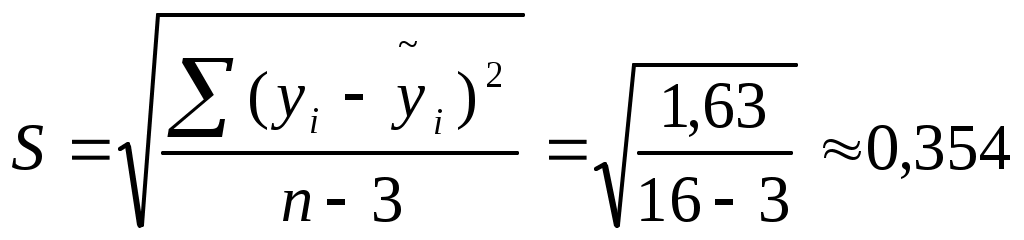
тогда




т.е. с надежностью 90% цена на поступившие автомобили попадет в интервал (17,92 ; 18,55).
3. Экономическая интерпретация.
Рассмотрим зависимость цены от возраста:

Так как = -0,856 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии .

Коэффициент формально определяет цену нового автомобиля, т.е. когда .

Коэффициент характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста автомобиля на 1 год следует ожидать уменьшения цены на 2,18 тыс. у.е.
Зависимость цены от мощности:

Так как = 0,819 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии .

Коэффициент характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении мощности автомобиля на 1 л.с следует ожидать увеличения цены на 0,104 тыс. у.е.
В результате исследования зависимости объема цены от двух факторов – возраста и мощности двигателя получено уравнение множественной регрессии

Коэффициент показывает, что при увеличении возраста на 1 год и неизменной мощности двигателя следует ожидать снижения цены автомобиля на 1,59 тыс. у.е.

Коэффициент показывает, что при увеличении мощности на 1 л.с и неизменном возрасте следует ожидать увеличения цены автомобиля на 0,07 тыс. у.е.

1   2   3   4

---

Задача 2

Временной ряд
В базе данных магазина также содержится информация об объеме ежемесячных продаж автомобилей за прошлый год, представленная в следующей таблице: (таблица 8)

месяц i	объем продаж, zi
1	208
2	209
3	239
4	263
5	274
6	293
7	258
8	293
9	321
10	307
11	324
12	324

1. 
   Представить графически ежемесячные объемы продаж автомагазина. На основе визуального анализа построенного графика выдвинуть гипотезу о виде статистической зависимости объема продаж от времени и записать ее математически.
   

Построим график ежемесячных продаж автомагазина:


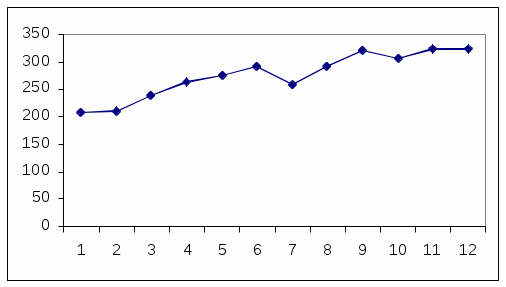
рис. 3 Траектория временного ряда
На основе визуального наблюдения ломанной линии динамики продаж можно выдвинуть гипотезу о наличии линейного тренда – устойчивого роста среднего уровня временного ряда.

Математически линейная зависимость выразится формулой , где - неизвестные параметры, - случайные возмущения.

2. 
   Методом наименьших квадратов найти оценку уравнения линейного тренда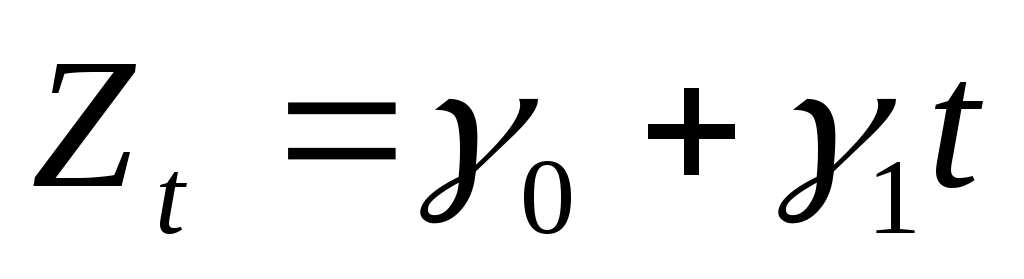
   

---

Составим вспомогательную таблицу: (таблица 9)

i	zi	ti2	zi ti
1	208	1	208
2	209	4	418
3	239	9	717
4	263	16	1052
5	274	25	1370
6	293	36	1758
7	258	49	1806
8	293	64	2344
9	321	81	2889
10	307	100	3070
11	324	121	3564
12	324	144	3888
78	3313	650	23084

т.к. n=12, то = = 276,08

= = 6,5

тогда


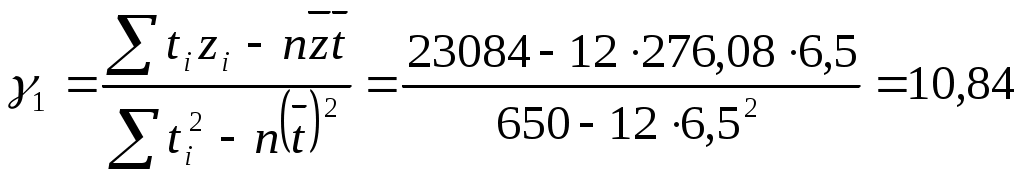
таким образом, получаем уравнение регрессии:


3. Для линии тренда построить доверительную полосу надежности 0,95. Нарисовать ее на графике вместе с линией тренда и исходным временным рядом.

Для расчета доверительных интервалов составим следующую таблицу: (таблица 10)

t	zt	Zt	zt -Zt	(zt -Zt )2	ti -tср	(ti -tср)2	Sz	Zн	Zв
1	208	216,46	-8,46	71,5716	-5,5	30,25	8,35	197,84	235,08
2	209	227,3	-18,3	334,89	-4,5	20,25	7,29	211,04	243,56
3	239	238,14	0,86	0,7396	-3,5	12,25	6,32	224,05	252,23
4	263	248,98	14,02	196,5604	-2,5	6,25	5,48	236,76	261,2
5	274	259,82	14,18	201,0724	-1,5	2,25	4,84	249,03	270,61
6	293	270,66	22,34	499,0756	-0,5	0,25	4,48	260,67	280,65
7	258	281,5	-23,5	552,25	0,5	0,25	4,48	271,51	291,49
8	293	292,34	0,66	0,4356	1,5	2,25	4,84	281,55	303,13
9	321	303,18	17,82	317,5524	2,5	6,25	5,48	290,96	315,4
10	307	314,02	-7,02	49,2804	3,5	12,25	6,32	299,93	328,11
11	324	324,86	-0,86	0,7396	4,5	20,25	7,29	308,6	341,12
12	324	335,7	-11,7	136,89	5,5	30,25	8,35	317,08	354,32
Σ				2361,058		143

---

Смотрите также файлы

• Основные направления социальной поддержки мигрантов в рф.docx

• Лабораторная работа 8 по дисциплинам Механическое оборудование карьеров иГорные машины Автогрейдеры.docx

• Тесты по фарме.docx

• московский международный университет Кафедра.docx

• Гласные и согласные звуки и буквы. Звукобуквенный анализ и синтез слов.doc