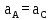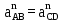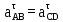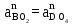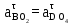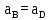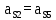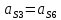ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.10.2024
Просмотров: 21
Скачиваний: 0
СОДЕРЖАНИЕ
1.1 Построение структурной схемы механизма
1.2 Определение степени подвижности механизма
1.3 Разбивка кинематической цепи механизма на структурные группы
1.4 Формула строения механизма
4.3 Определение уравновешивающей силы методом «жесткого рычага» н.Е. Жуковского
4.4 Сравнение результатов кинетостатического анализа
4.5 Определение угловых скоростей в кинематических парах
4.6 Определение потерь мощности
4.7 Расчет приведенного момента инерции
Таким образом, все поставленные задачи решены в заданном объеме. Список использованных источников
-
Построение плана ускорений
Абсолютное ускорение точки A, принадлежащей звену AO, определяется по формуле
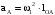 ,
(2.6)
,
(2.6)
где ω1 – угловая скорость звена OA, рад/с.
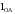 -
длина звена OA,
м.
-
длина звена OA,
м.
Подставляя исходные данные в формулу (2.6), определим модуль ускорения точки A
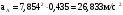 .
.
Масштаб плана ускорений μа вычисляется по формуле
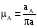 ,
(2.7)
,
(2.7)
где аА - модуль абсолютного ускорения точки А, м/с2;
πa – отрезок на плане ускорений, мм.
Ускорению точки А, равному 26,833 м/с2, на чертеже соответствует отрезок 44,716 мм. Таким образом, масштаб плана ускорений будет равен
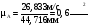 .
.
Для определения ускорения точки В составим систему векторных уравнений:
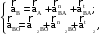 (2.8)
(2.8)
где
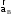 – вектор ускорения точки В, м/с2;
– вектор ускорения точки В, м/с2;
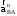 ,
,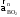 –
вектора нормального
ускорения точки В в
относительном движении,
направленные по радиусам вращения (BА
и ВО2)
к центрам вращения А и О2
соответственно, м/с2;
–
вектора нормального
ускорения точки В в
относительном движении,
направленные по радиусам вращения (BА
и ВО2)
к центрам вращения А и О2
соответственно, м/с2;
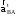 ,
,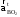 –
вектора касательного ускорения точки
В в относительном движении, направленные
перпендикулярно
радиусам вращения BА
и ВО2
соответственно,
м/с2;
–
вектора касательного ускорения точки
В в относительном движении, направленные
перпендикулярно
радиусам вращения BА
и ВО2
соответственно,
м/с2;
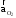 – ускорение
точки О2
(равно 0), м/с2.
– ускорение
точки О2
(равно 0), м/с2.
Величины нормальных ускорений звеньев определяем по формуле
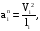 (2.10)
(2.10)
где Vi – скорость движения точки соответствующего звена, м/с;
li – длина соответствующего звена, м.
Подробно опишем построение плана ускорений.
Результаты вычисления приведены в таблице 2.4.
Отмечаем
некоторую точку
(полюс). Чтобы построить вектор
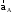 ,
откладываем отрезок, равный 44,716 мм.
Параллельно звену OA
по направлению от А к O
и получаем точку а. Из точки а откладываем
вектор
,
откладываем отрезок, равный 44,716 мм.
Параллельно звену OA
по направлению от А к O
и получаем точку а. Из точки а откладываем
вектор
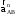 .
Из конца вектора
.
Из конца вектора
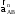 проводим прямую, перпендикулярную звену
АВ. Из
откладываем вектор
проводим прямую, перпендикулярную звену
АВ. Из
откладываем вектор
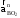 .
Из конца вектора
.
Из конца вектора
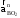 проводим прямую перпендикулярно звену
ВО2.
На пересечении прямых получаем точку
b.
Из полюса в точку b
проводим вектор, который будет являться
вектором
проводим прямую перпендикулярно звену
ВО2.
На пересечении прямых получаем точку
b.
Из полюса в точку b
проводим вектор, который будет являться
вектором
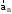 .
.
Угловые ускорения звеньев в данном положении могут быть найдены по формулам
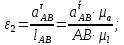 (2.12)
(2.12)
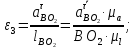 (2.13)
(2.13)
Подставив значения в уравнения, получим:
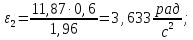
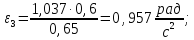 Аналогично
проводим построения для нижней части
рычажного механизма летучих ножниц.
Аналогично
проводим построения для нижней части
рычажного механизма летучих ножниц.
Таблица 2.4 – Результаты вычислений ускорений точек, угловых ускорений звеньев
|
Величина |
Размер на чертеже, мм |
Действительный размер, м/с2 |
|||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
1 |
2 |
3 |
4 |
5 |
||
|
|
44,72 |
44,72 |
44,72 |
44,72 |
44,72 |
44,72 |
26,833 |
26,833 |
26,833 |
26,833 |
26,833 |
26,833 |
|
|
|
0,79 |
21,16 |
36,41 |
3,41 |
0,00 |
0,26 |
0,476 |
12,696 |
21,848 |
2,044 |
0,002 |
0,158 |
|
|
|
91,75 |
96,59 |
56,59 |
92,35 |
22,67 |
11,88 |
55,053 |
57,956 |
33,952 |
55,411 |
13,601 |
7,126 |
|
|
|
36,81 |
63,32 |
37,93 |
5,79 |
29,15 |
33,71 |
22,086 |
37,989 |
22,761 |
3,476 |
17,487 |
20,225 |
|
|
|
33,66 |
18,13 |
101,54 |
95,98 |
17,03 |
1,04 |
20,196 |
10,875 |
60,921 |
57,590 |
10,216 |
0,622 |
|
|
|
49,88 |
65,86 |
108,39 |
96,16 |
33,75 |
33,72 |
29,928 |
39,515 |
65,034 |
57,695 |
20,253 |
20,234 |
|
|
|
11,80 |
26,91 |
75,78 |
59,06 |
37,96 |
39,16 |
7,078 |
16,147 |
45,467 |
35,436 |
22,778 |
23,495 |
|
|
|
24,94 |
32,93 |
54,20 |
48,08 |
16,88 |
16,86 |
14,964 |
19,758 |
32,517 |
28,847 |
10,126 |
10,117 |
|
|
|
- |
- |
- |
- |
- |
- |
28,088 |
29,569 |
17,323 |
28,271 |
6,939 |
3,636 |
|
|
|
- |
- |
- |
- |
- |
- |
31,071 |
16,731 |
93,725 |
88,600 |
15,717 |
0,957 |
|
-
Построение кинематических диаграмм
Выходным звеном исследуемого механизма является нож, жестко закрепленный с шатуном АВ и CD. Построив планы механизма, мы тем самым разметили путь ножа в соответствии с углами поворота кривошипа. Построим кинематическую диаграмму вертикальных перемещений указанного звена (SН=SН(t)).
Масштабный коэффициент перемещений μS диаграммы SН = SН(t)
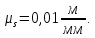 (3.2)
(3.2)
Строим оси координат SН − t и на оси абсцисс откладываем отрезок l=240 мм, изображающий время одного полного оборота кривошипа в масштабе времени μt.
Таким образом, масштабный коэффициент времени
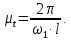 (3.5)
(3.5)
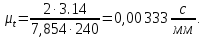
Отрезок l делим на 12 равных частей и в соответствующих точках 1,2,3, …, 12 по оси ординат откладываем расстояния, пройденные ножом от её начального (крайнего верхнего) положения на плане положений механизма.
Соединив последовательно плавной кривой полученные точки 0, 1’, 2’, …, 12, получим диаграмму перемещений звена 5.
Для построения диаграммы скоростей выходного звена (VН=VН(t)) под диаграммой перемещений строим оси координат VН − t и на продолжении оси абсцисс откладываем влево от начала координат отрезок произвольной длины (примем H1 = O1P1 = 40 мм).
Из точки P1 проводим лучи P11’, P12’, P13’, … параллельно хордам кривой S − t на участках 01’, 1’2’, 2’3’, … . Эти лучи отсекут на оси ординат диаграммы скоростей отрезки O11’, O12’, O13’, …, пропорциональные средней скорости VН на соответствующем участке диаграммы.
Отложим эти отрезки на средних ординатах соответствующих участков.
Соединив ряд полученных точек 0, 1’’, 2’’, 3’’, …, 12 плавной кривой, получим диаграмму скорости VН − t.
Для построения диаграммы ускорения выходного звена 5 под диаграммой скоростей строим оси координат aН − t и на продолжении оси абсцисс откладываем влево от начала координат отрезок произвольной длины (примем H2 = O2P2 = 40 мм).