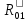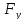ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.10.2024
Просмотров: 23
Скачиваний: 0
СОДЕРЖАНИЕ
1.1 Построение структурной схемы механизма
1.2 Определение степени подвижности механизма
1.3 Разбивка кинематической цепи механизма на структурные группы
1.4 Формула строения механизма
4.3 Определение уравновешивающей силы методом «жесткого рычага» н.Е. Жуковского
4.4 Сравнение результатов кинетостатического анализа
4.5 Определение угловых скоростей в кинематических парах
4.6 Определение потерь мощности
4.7 Расчет приведенного момента инерции
Таким образом, все поставленные задачи решены в заданном объеме. Список использованных источников
Из точки P2 проводим лучи P21, P22, P23, … параллельно хордам кривой VН − t на участках 01’’, 1’’2’’, 2’’3’’, … . Эти лучи отсекут на оси ординат диаграммы ускорений отрезки O21’’, O22’’, O23’’, …,пропорциональные среднему ускорению aН на соответствующем участке диаграммы. Соединив ряд полученных точек плавной кривой, получим диаграмму ускорений aН − t.
Масштабный коэффициент для диаграммы скоростей и ускорений равен
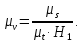 (3.6)
(3.6)
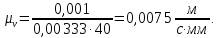
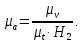 (3.7)
(3.7)
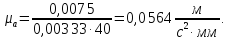
-
Кинетостатический анализ рычажного механизма
При силовом расчете механизма используется метод кинетостатики, основанный на принципе Д’Аламбера. В соответствии с указанным принципом, в дополнение ко всем действующим на механизм внешним силам, необходимо приложить силы и моменты сил инерции звеньев, чтобы привести механизм в состояние равновесия. После приведения механизма в равновесие для расчетов применяются уравнения статики.
Задачами кинетостатического анализа являются:
- определение сил инерции звеньев и точек их приложения, моментов сил инерции звеньев;
- определение весов звеньев механизма;
- определение уравновешивающей силы.
Для определения уравновешивающей силы будем использовать метод планов сил Н.Г. Бруевича и метод «жесткого рычага» Н.Е Жуковского.
-
Определение сил инерции звеньев и точек их приложения, моментов сил инерции звеньев
Рассмотрим заданное положение механизма.
Так как в данном механизме симметрично расположены звенья, и усилие резания прикладывается одинаково к верхнему и нижнему ножу, то достаточно будет провести расчет для верхней кинематической цепи механизма.
Зная положения точек S1, S2, S3 на планах ускорений, определим силы инерции звеньев по следующей формуле:
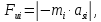
где m???? – масса i-го звена, кг;
????S???? - ускорение центра масс i-го звена, м/с2.
Знак «-» указывает на то, что вектор силы инерции Fu???? направлен противоположно вектору ускорения ????s???? .
Результаты расчетов приведены в таблице 3.2.
Момент силы инерции звеньев определим по формуле:
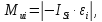
где
IS????
=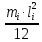 –
момент
инерции
i-го
звена
относительно
оси,
проходящей
через
центр
масс,
кг
∙
м2;
–
момент
инерции
i-го
звена
относительно
оси,
проходящей
через
центр
масс,
кг
∙
м2;
???????? – угловое ускорение i-го звена, рад/с2.
Знак «-» указывает на то, что момент силы инерции Ми???? направлен противоположно угловому ускорению ???????? .
Определим веса звеньев механизма по формуле:
G???? = m???? ????,
где m???? – масса i-го звена, кг;
???? – ускорение свободного падения, равное 9,81 м/с2.
Результаты расчетов приведены в таблице 4.2.
Таблица 4.2 – Результаты расчетов, необходимые для кинетостатического анализа
|
№ звена |
Масса звена m????, кг |
Момент инерции звена IS????, кг∙м2 |
Вес звена G???? , Н |
Вектор ускорения центра масс ????????????????, мм |
Ускорение центра масс ????????????, м/с2 |
Сила инерции Fu???? , Н |
Момент сил инерции Мu????, Н·м |
Сила полезного сопротивления FC , кН |
|
1 |
- |
- |
- |
- |
- |
- |
|
- |
|
2 |
650 |
208,09 |
6376,5 |
46,803 |
23,40 |
15211,0 |
742,04 |
- |
|
3 |
320 |
11,27 |
3139,2 |
19,993 |
10,00 |
3198,9 |
46,43 |
305,26 |
-
Определение уравновешивающей силы методом планов сил н.Г. Бруевича
Силовой расчет механизма методом планов сил сводится к определению уравновешивающей силы путем последовательного расчета реакций в кинематических парах механизма. Определение реакций в кинематических парах начинаем с анализа последней (считая от ведущего звена) присоединенной группы, затем последовательно переходим к следующей группе и заканчиваем силовой расчет анализом ведущего звена. Порядок силового расчета рассмотрим для заданного положения механизма.
Рассмотрим группу, состоящую из звеньев 2 и 3. На звенья этой группы действуют реакции R03 и R12
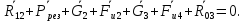
Реакция R03 проходит через центр шарнира О2 она неизвестна ни по величине, ни по направлению. Реакция R12 прикладывается в центре вращательной пары ????.
Чтобы определить реакцию R12, действующую в паре А, разложим ее на две составляющие:
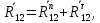
Чтобы определить реакцию R03, действующую в паре О2, разложим ее на две составляющие:
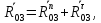
Величина
силы
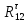 определяется из уравнения моментов
всех сил действующих на звено 2 относительно
точки B.
определяется из уравнения моментов
всех сил действующих на звено 2 относительно
точки B.
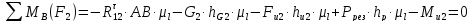
откуда
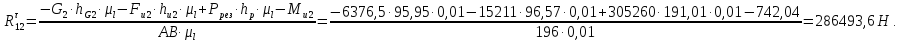
Величина
силы
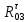 определяется из уравнения моментов
всех сил действующих на звено 3 относительно
точки B.
определяется из уравнения моментов
всех сил действующих на звено 3 относительно
точки B.
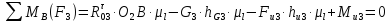
откуда
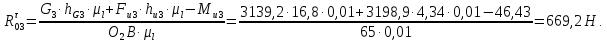
Реакцию
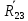 в
паре 2 – 3 определяем из условия равновесия
шатуна
АВ:
в
паре 2 – 3 определяем из условия равновесия
шатуна
АВ:
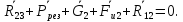
Строим
план сил для диады 2-3. Масштабный
коэффициент диады:
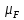
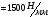 ;
;
Результаты расчетов представлены в таблице 4.4.
Таблица 4.4 - Результаты силового расчета группы, состоящей из звеньев 2, 3
|
Обозначение силы |
Длина вектора, мм |
Величина силы, Н |
|
R12 |
194,96 |
292440 |
|
R03 |
10,49 |
15735 |
|
R23 |
6,648 |
9972 |
Рассмотрим равновесие ведущего звена – кривошипа 1. Условие равновесия для кривошипа запишется следующим образом:
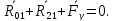
В данном уравнении неизвестна величина силы Fу, величина и линия действия силы R01. Чтобы определить реакцию R01 в шарнире ????, разложим ее на две составляющие:
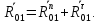
Составим уравнение моментов всех сил, действующих на звено 1, относительно точки ????.
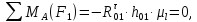
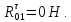
Тогда условие равновесия для кривошипа 1 запишется:
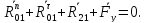
Решаем
графически уравнение, построив план
сил. Из начала вектора
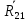 проводим
линию
действия силы
проводим
линию
действия силы
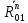 ,
параллельную кривошипу 1, а из конца
вектора
,
параллельную кривошипу 1, а из конца
вектора
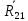 проводим
линию
действия
силы
проводим
линию
действия
силы
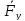 ,
перпендикулярную
к кривошипу 1. Пересечение двух линий
определяет
положение
конца
вектора
,
перпендикулярную
к кривошипу 1. Пересечение двух линий
определяет
положение
конца
вектора
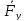 и
начало вектора
и
начало вектора
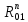 =
=
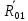 .
Масштабный коэффициент сил для данной
группы
.
Масштабный коэффициент сил для данной
группы
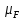
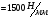 ;
;
Результаты вычислений приведены в таблице 4.5.
Таблица 4.5 – Результаты силового расчета ведущего звена
|
Обозначение силы |
Длина вектора, мм |
Величина силы, Н |
|
|
183,37 |
275055 |
|
|
66,22 |
99330 |