Файл: Poyasnitelnaya_zapiska-2.docx

Содержание

Введение

_{1.Структурный анализ рычажного механизма}

_{1.1 Построение структурной схемы механизма}

_{1.2 Определение степени подвижности механизма}

_{1.3 Разбивка кинематической цепи механизма на структурные группы}

_{1.4 Формула строения механизма}

_{2 Кинематический анализ рычажного механизма}

_{2.1 Построение плана положений рычажного механизма}

_{2.2 Построение планов скоростей}

_{2.3 Построение плана ускорений}

_{3. Построение кинематических диаграмм}

_{4. Кинетостатический анализ рычажного механизма}

_{4.1 Определение сил инерции звеньев и точек их приложения, моментов сил инерции звеньев}

_{4.2 Определение уравновешивающей силы методом планов сил Н.Г. Бруевича}

_{4.3 Определение уравновешивающей силы методом «жесткого рычага» Н.Е. Жуковского}

_{4.4 Сравнение результатов кинетостатического анализа}

_{4.5 Определение угловых скоростей в кинематических парах}

_{4.6 Определение потерь мощности}

4.7 Расчет приведенного момента инерции

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Введение

Сила резания Р_рез всегда направлена вертикально. Ножи H жестко закреплены на шатунах AB и CD и в вертикальном положении кривошипов при резании совпадают с ними по направлению.

Привод ножей осуществляется через два кривошипно-ползунных механизма. O₁ABO₂ и O₃CDO₄. Общий привод осуществляется от электродвигателя через планетарный редуктор и зубчатую передачу z₅-z₆ к кривошипам 1 и 4.

В состав механизма входит кулачковый механизм подъемного рольганга с приводом от зубчатых колес z₅-z₆.

1. Структурный анализ рычажного механизма

Задачами структурного анализа исследуемого рычажного механизма являются:

• построение структурной схемы механизма;

• определение степени подвижности механизма;

• разбивка кинематической цепи механизма на структурные группы;

• определение формулы строения механизма.

1.1 Построение структурной схемы механизма

---

Структурная схема механизма представлена на рисунке 1.1.

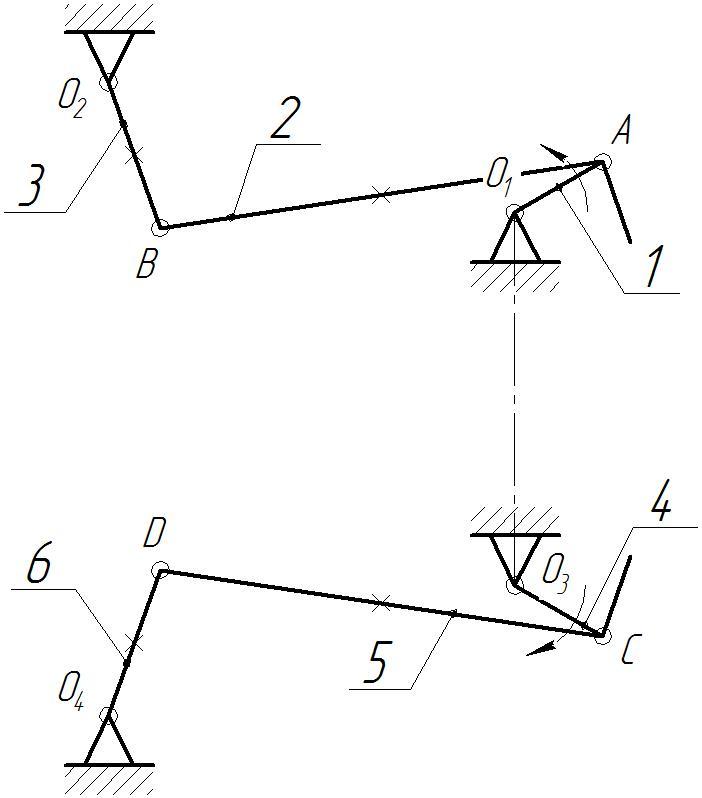
Рисунок 1.1 – Структурная схема рычажного механизма

Так как данный рычажный механизм состоит из двух независимых, симметричных кинематических цепей, то их расчет и анализ эквивалентен. В дальнейшем условимся рассматривать верхнюю кинематическую цепь.

Механизм состоит из четырех звеньев. Примем следующие условные обозначения звеньев механизма: 0 – стойка; 1 – кривошип; 2 – шатун; 3 – коромысло. Таким образом, количество подвижных звеньев равно 3-ти.

Звенья механизма соединены между собой кинематическими парами. Все пары низшие (вращательные и поступательные), плоские.

Обозначим кинематические пары: 1) стойка 0 образует с кривошипом 1 вращательную пару О; 2) кривошип 1 с шатуном 2 – вращательную пару А; 3) шатун 2 с коромыслом 3 - вращательную пару B; 4) коромысло 3 со стойкой 0 – вращательную пару О₂. Таким образом, количество низших пар (пар пятого класса) 4. Высшие пары (пары четвертого класса) отсутствуют.

1.2 Определение степени подвижности механизма

Степень подвижности механизма определяем по формуле Чебышева П.Л. для плоских механизмов

W = 3n – 2p₅ − p₄ = 3n – 2p_н − p_в, (1.1)

где n - число подвижных звеньев;

p_н - число низших кинематических пар (пятого класса);

p_в- число высших кинематических пар (четвертого класса).

Для исследуемого механизма степень подвижности

W = 3 ∙ 3 − 2 ∙ 4 − 0 = 1.

---

1.3 Разбивка кинематической цепи механизма на структурные группы

Составим структурные группы механизма и определим класс и вид групп согласно классификации Л.В. Ассура.

Так как степень подвижности механизма W = 1, механизм имеет одно входное звено – звено 1, закон движения которого задан. Входное звено 1 со стойкой 0 составляют начальный механизм (механизм I-го класса). Схема механизма первого класса изображена на рисунке 1.2.

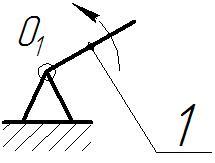
Рисунок 1.2 – Схема механизма первого класса

Шатун 2 и коромысло 3 образуют структурную группу II-го класса. Эта группа включает в себя три кинематические пары: А, В и О₂. Поскольку все три вращательные пары А, В и О₂ – внешние, это группа 1-го вида. Схема данной структурной группы изображена на рисунке 1.3.

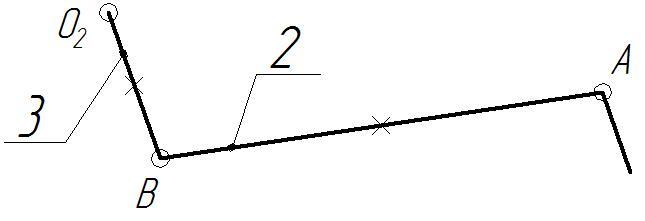
Рисунок 1.3 – Схема структурной группы II-го класса 1-го вида, образованной звеньями 2 и 3

Таким образом, исследуемый механизм, обладающий одной степенью подвижности, можно рассматривать как образованный путем последовательного присоединения к стойке 0 и ведущему звену 1 группы, состоящих из звеньев 2, 3. По классификации Л.В. Ассура он должен быть отнесен к механизму II-го класса.

1.4 Формула строения механизма

Формула строения механизма имеет вид

I→II₁.

Таким образом, исследуемый механизм II-го класса.

2. Кинематический анализ рычажного механизма

   1. Построение плана положений рычажного механизма

Построим план положений рычажного механизма в 12 положениях. Параметры механизма приведены в таблице 2.1.

Таблица 2.1 – Геометрические параметры исследуемого механизма

Действительные размеры, мм
O1A= O3С	AB=CD	BО2= DО4	X	Y	LH
0,435	1,96	0,65	1,73	0,545	0,4
Размеры на чертеже, мм
O1A= O3С	AB=CD	BО2= DО4	X	Y	LH
43,5	196	65	173	54,5	40

---

Принимаем размер кривошипа 1 на чертеже равным 43,5 мм, т.е. ОА=43,5 мм. Определяем масштабный коэффициент по формуле

_l=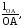 (2.1)

Подставив данные, получим

.

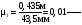2. Построение планов скоростей

Определяем для этого положения механизма скорость точки A по формуле

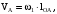(2.2)

где 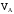− скорость точки А, м/с;

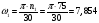− угловая скорость ведущего звена OА, рад/с;

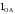− истинная длина звена OА, м.

Подставив значения в формулу (4.2) получим выражение для нахождения скорости

.

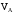
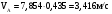Скорость точки A направлена перпендикулярно линии OA в сторону, соответствующей направлению угловой скорости звена 1. Угловая скорость кривошипа постоянна, т.е. кривошип OA движется равномерно.

Строим план скоростей. Для этого выберем произвольную точку p, из которой отложим отрезок pa, изображающий скорость 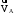. Отрезок 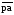откладываем перпендикулярно линии OА, длину отрезка 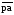выбираем равной 68,33 мм и определяем масштаб плана скоростей по формуле

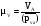. (2.3)

Подставив численные значения, получим

.

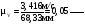Построим план скоростей механизма, для положения 5. Составим систему векторных уравнений для определения скорости точки В

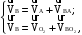(2.4)

где 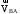− вектор скорости точки В при вращении звена 2 относительно точки А, направлена перпендикулярно звену АВ, м/с;

---

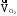− скорость точки О₂, м/с (равна 0, так как О₂ – опорная точка);

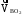− скорость точки В при вращении звена 3 относительно покоящейся точки О₂, направлена перпендикулярно звену BО₂, м/с.

Строим решение векторного уравнения (2.4) через точку а проведем прямую перпендикулярную АВ. Т.к. скорость точки О₂ равна 0, то точку с помещаем в полюс. Через полюс проведем прямую перпендикулярную ВО₂. Точка b является пересечением двух векторов аb и p_vb, изображающие скорост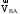и и 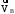соответственно.

Угловые скорости звеньев в данном положении могут быть найдены по формулам

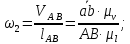(2.5)

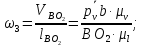(2.6)

ω₅ = 0, так как звено 5 совершает только возвратно-поступательное движение.

Подставив значения в уравнения (2.5), (2.6), получим

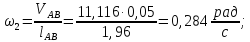
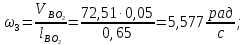
Если вектор ab перенести в точку B звена 3, то он укажет направление вращения кулисы относительно точки А, а, следовательно, и направление ω₂.

Если вектор p_vb перенести в точку B звена 3, то он укажет направление вращения кулисы относительно оси 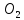, а, следовательно, и направление ω₃.

Значения скоростей определяем, измерив длину соответствующих скоростям векторов и умножив их на масштаб плана скоростей.

Аналогично проводим построения для нижней части рычажного механизма летучих ножниц.

Таблица 2.2 – Результаты вычислений скоростей точек звеньев

Величина	Положение
	0	1	2	3	4	5	6	7	8	9	10	11
VA=VС	3,416	3,416	3,416	3,416	3,416	3,416	3,416	3,416	3,416	3,416	3,416	3,416
VAB=VСD	0,966	4,988	6,544	2,001	0,062	0,556	1,041	1,698	2,598	3,378	3,323	1,948
VB=VD	3,789	4,969	3,846	1,503	3,371	3,626	3,383	2,724	1,579	0,130	1,243	2,488
VS2=VS5	3,575	3,459	1,590	2,442	3,394	3,512	3,360	2,971	2,323	1,730	1,962	2,825
VS3=VS6	1,894	2,485	1,923	0,752	1,686	1,813	1,692	1,362	0,789	0,065	0,621	1,244
ω2=ω5	0,493	2,545	3,339	1,021	0,031	0,284	0,531	0,866	1,325	1,723	1,695	0,994
ω3=ω6	5,829	7,645	5,917	2,312	5,187	5,578	5,205	4,190	2,429	0,200	1,912	3,828

---