ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РАСЧЁТ ПОЛОГИХ ОБОЛОЧЕК ПО БЕЗМОМЕНТНОЙ ТЕОРИИ
Нуманов О.Р. Набизода М.Ш., Сангинов А.С.
(ТТУ им. академика М.С. Осими, г. Душанбе)
Аннотация. В данной статье приведены расчёт отдельностоящих и неразрезных пологих оболочек положительной кривизны по безмоментной теории.
Ключевые слова. Пологая оболочка, неразрезность, безмоментная теория, деформация, усилия, нагрузка, линейная теория, нелинейная теория, диафрагма.
Расчёт пологих оболочек двоякой кривизны по безмоментной теории производят при (dz/dx)2«1. (dz/dу)2«1. Пренебрегая квадратами производных и их произведениями, т. е. считаем ds1 ≈ dx и ds2 ≈ dу.
Таким образом, условия равновесия пространственного элемента оболочки могут быть заменены условиями равновесия его горизонтальной проекции.
В зависимости от степени пологости и характера нагрузки расчет пологих оболочек может производиться по безмоментной или моментной упругой теории, при этом и безмоментное и моментное теории могут быть линейными и нелинейными [1].
Так как нелинейная теория учитывает вертикальные деформации (прогибы) оболочки под воздействием нагрузки, то расчёт по этой теории следует вести только для весьма пологих оболочек, в которых подъём соизмерим с их толщиной и прогибом, т.е. при f/δ
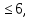 где f= f1+ f2.
где f= f1+ f2.Очевидно, что нелинейные факторы ухудшают условия работы оболочки, поэтому рекомендуется избегать таких конструкций оболочек с весьма малыми подъёмами.
В работе [2] предложен метод, позволяющий более точно решать вопрос о том, что какой способ расчёта применить к той или иной оболочке – по линейной теории или по нелинейной. Для этого по нелинейной теории определяют прогиб от расчётной нагрузки в середине оболочки.
После этого также определяют нагрузку в середине оболочки, только по линейной теории. Необходимо отметить, что при равных прогибах нагрузка, вычисленная по линейной теории, будет больше нагрузки, вычисленной по нелинейной теории. Если соотношение нагрузок k= qл /q <1,05, расчёт можно производить по линейной теории, если же k= qл /q >1,05, т.е. разница между нагрузками существенна, расчёт надо производить по нелинейной теории.
Расчёт тонких оболочек с относительно большим подъёмом при равномерно распределённой нагрузке можно выполнять по безмоментной линейной теории.
Учёт изгибающих моментов необходимо производить только вблизи опорного контура.
Пренебрегая при расчёте оболочек изгибающими моментами, мы тем самым пренебрегаем тангенциальными деформациями срединной поверхности, учитывая только её вертикальные перемещения.
Далее коротко изложим метод расчёта тонких пологих оболочек положительной гауссовой кривизны по безмоментной линейной теории. Рассмотрение условий равновесия элемента оболочки, находящегося под действием вертикальной нагрузки q, приводит к трём дифференциальным уравнениям равновесия:
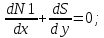
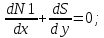
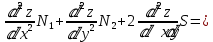 q. (1)
q. (1)Третье уравнение (1) легко можно быть преобразовано и намного упрощено для эллиптического параболоида. При этом смешанная производная обращается в нуль, а вторые производные по х и у есть не что иное, как кривизны главных парабол в вершине оболочки, т.е. главные её кривизны.
Таким образом, окончательно имеем:
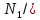 r1 +
r1 +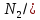 r2 = q. (2)
r2 = q. (2)Уравнение (2) является уравнением равновесия всех сил, спроектированных на вертикальную ось. При расчёте оболочек с поверхностью эллиптического параболоида приближенно полагают кривизны оболочки постоянными, равными её главным кривизнам, что позволяет применять (2) для любой точки поверхности.
Пользуясь (1), можно дать решение неизвестных усилий N1, N2 и S в виде бесконечных рядов. Для этого вводят функцию напряжений F так, что r1
N1=
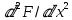 ; N2=
; N2=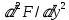 ; S=
; S=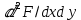 . (3)
. (3)Легко видеть, что выражение (3) удовлетворяют первым двум уравнениям (1).
Подставляя функцию F в (2), получаем:
1/r1·
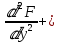
1/r2·
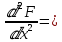 q. (4)
q. (4)Произведя замену переменных:
у=η/
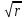 1 ; х=ξ/
1 ; х=ξ/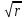 2 ,
2 ,получим гармоническое уравнение Пуассона:
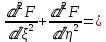 q. (5)
q. (5)При решении уравнения (5) необходимо учитывать условия закрепления оболочки на её контуре (условия неразрезности).
Необходимо отметить, что на краю безмоментной оболочки мы вправе распоряжаться только теми усилиями или перемещениями, которые действуют по касательной к поверхности.
Для отдельно стоящих оболочек контурные диафрагмы обычно предполагаются абсолютно жёсткими в вертикальной плоскости и податливыми из неё. Такой вид закрепления приводит к тому, что нормальные усилия, действующие перпендикулярно плоскости диафрагмы, обращаются на краю оболочки в нуль. Нагрузки от оболочки на диафрагмы передаются, таким образом, только через касательные усилия.
После постановки граничных условий решение может быть получено в двойных тригонометрических или, что удобнее, в одинарных гиперболо - тригонометрических рядах. Указанные формулы приведены в формулах 6.3 и 6.4 Руководства [3].
Необходимо отметить, что при расчёте отдельно стоящей оболочки по безмоментной теории делается предположение об абсолютной податливости контурных диафрагм в горизонтальном направлении по всей их длине. Эти граничные условия связываются с равенством нулю нормальных усилий на контуре, перпендикулярных краю оболочки.
Выше рассматривали условия расчёта отдельно стоящей оболочки со свободным опиранием по всему контуру. Между тем наиболее употребительной формой оболочек, применяемых для покрытия многопролётных зданий, являются многоволновые оболочки, обычно выполняемые как неразрезные (Рис. 1).
| 2а | 2а | 2а | 2а |
| | | | 2б |
| | | | 2б |
| 2а | 2а | 2а | 2а |
а) б)
Рис. 1. Многоволновые неразрезные железобетонные пологие
оболочки положительной гауссовой кривизны.
а) однорядные; б) многорядные. 2а и 2б размеры сторон оболочки
Условия закрепления на контуре неразрезных пологих оболочек, имеющих по линии сопряжения общую диафрагму, намного отличаются от условий закрепления одноволновых оболочек. В этом случае необходимо отличать однорядные (рис.1, а) и многорядные (рис.1, б) оболочки.
С достаточной для практики точностью можно полагать, что по внешним линиям контура неразрезных оболочек имеет место те же условия, что и на внешнем контуре отдельно стоящей оболочки, т.е. что на контуре отсутствуют нормальные усилия, направленные перпендикулярно оси диафрагмы, а сама диафрагма, будучи абсолютно жесткой в своей плоскости, не сопротивляется усилиям, стремящимся вывести её из плоскости. Соединение оболочки с диафрагмой по-прежнему предполагается шарнирным.
Диафрагмы в виде арок, балок, ферм, а также криволинейных брусьев на ряды колонн, расположенные по внутренним контурам, т.е. общие для двух соседних оболочек, можно приближённо полагать несмещающимися как в своей плоскости, так и из неё. Очевидно, что в этом случае нормальные усилия, направленные поперёк оси диафрагмы, не обращаются в нуль. Присоединение оболочки к диафрагме предполагается жёстким (заделка).
1 2 3 4 5 6





 х х х х х х
х х х х х х










 а
а 





 а у у у у у у
а у у у у у у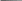
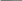
b b


Рис. 2. Граничные условия неразрезных железобетонных
пологих оболочек покрытия
Исходя из вышеуказанного, задача о расчёте неразрезных пологих оболочек положительной гауссовой кривизны может быть приближённо сведена к расчёту одноволновых оболочек с различными контурными закреплениями. На рис. 2 показаны шест случаев контурных закреплений (двойной линией обозначен контур, условно не смещаемый в горизонтальном направлении).
Решение для первого случая (отдельно стоящая оболочка) было дано выше. Решение средней оболочки (случай 6) приводит к весьма простым результатам – сдвигающие усилия на всей её поверхности обращаются в нуль, а нормальные усилия приобретают вид:
N1=- qr1
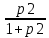 ; N2=- qr1
; N2=- qr1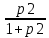 , (6)
, (6)где p=r2/r1=k1/k2.
Нормальные сжимающие усилия постоянны по всей поверхности оболочки. При равных кривизнах (р=1)
N1= N2=-
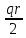 . (6а)
. (6а)Второй случай граничных условий даёт следующие значения усилий (обращаем внимание на положение координатных осей на рис. 2, 2):

