ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
N1=-
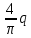 r1
r1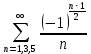 х
х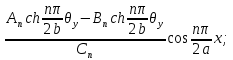
S=-
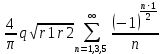 х
х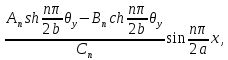 (7)
(7)где An=2p2 sh nπ
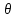 -(1-p)2 nπ
-(1-p)2 nπ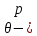 2-2p-1) th nπ
2-2p-1) th nπ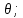
Вn=2p2 (ch nπ
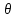 -1)-(1-p)2 nπ
-1)-(1-p)2 nπ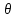 th nπ
th nπ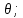
Cn=(1+p)2 sh nπ
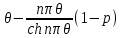 2;
2;p= k1/k2=r2/r1.
Третий случай граничных условий:
N1=-
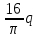 r1p2
r1p2 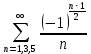 х
х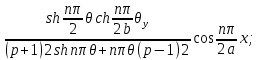
S=-
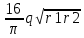
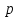 2
2 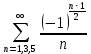 х
х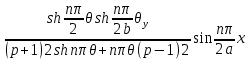 . (8)
. (8)Формулы для четвёртого и пятого случаев, с целью упрощения, приведены для сферической поверхности, когда р=1, т.е. r1 = r2 = r.
Четвёртый случай граничных условий:
N1=

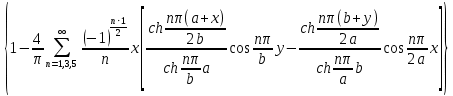 ;
;S=
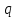 r
r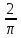
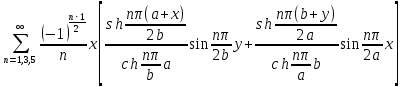 . (9)
. (9)Пятый случай граничных условий:
N1=

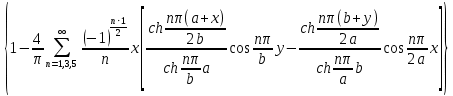 ;
;S=
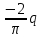 r
r 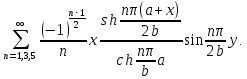 (10)
(10)Расчёт оболочки для третьего случая граничных условий обычно может быть выполнен посредством тех же таблиц коэффициентов
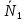 и
и 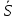 , с помощью которых рассчитываются свободно стоящие оболочки.
, с помощью которых рассчитываются свободно стоящие оболочки.Действительно, первую формулу системы (8) можно преобразовать, представив входящий в неё гиперболо-тригонометрический ряд в виде произведения другого ряда, входящего в уравнение 1V.12 [1] для отдельно стоящей оболочки, нагруженной равномерно распределённой нагрузки
 и множителя χ. Искомый множитель χ, представляющий собой частное от деления двух рядов, сходится весьма быстро.
и множителя χ. Искомый множитель χ, представляющий собой частное от деления двух рядов, сходится весьма быстро.χ=
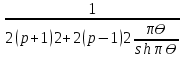 . (11)
. (11)Тот же коэффициент аналогичным образом может быть получен для сдвигающих усилий.
Теперь можно написать выражение для безмоментных компонент усилий для третьего случая граничных условий, пользуясь известными таблицами коэффициентов
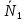 и
и 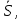 составленными для свободно стоящей оболочки:
составленными для свободно стоящей оболочки:N1=
 r1
r1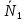 χ, N2=
χ, N2=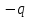 r2(1-
r2(1-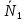 χ), S=
χ), S=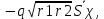 (12)
(12)где
χ=4p2 χ=
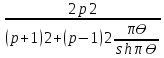 . (13)
. (13)Выше отмечалось, что выражение для поправки сходится весьма быстро. Сходимость поправки зависит лишь от геометрических параметров оболочки pи
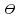 , входящих в (13).
, входящих в (13).Имея решение для отдельно стоящих оболочек (случай 1) и для средних ячеек многоволновых оболочек (случай 3 и 6), можно приближённо рассчитать оболочки с любыми граничными условиями, не прибегая к (7), (9) и (11).
Так, например, при системе неразрезных однорядных оболочек (рис. 1, а) расчленим мысленно крайнюю оболочку по её оси на две половины. Та её половина, которая примыкает к свободному наружному краю, может быть приближённо рассчитана и сконструирована как отдельно стоящая оболочка; та же половина оболочки, которая примыкает к соседней средней ячейке и имеет с ней общую диафрагму, может быть рассчитана и сконструирована как средняя оболочка (случай 3 граничных условий).
При проектировании неразрезных многоволновых оболочек надо обращать внимание на следующее обстоятельство: две соседние оболочки, имеющие общую диафрагму, испытывают взаимное давление по линии их сопряжения (поскольку по внутренним краям усилия, направленные нормально к ним, вообще говоря, не равны нулю).
В средних ячейках оболочек (случай 3 и 6) боковые давления на её противоположных краях уравновешиваются. Другое дело – в крайних и угловых ячейках (случай 2, 4 или 5), где боковое давление соседней оболочки не уравновешивается на противоположном, свободном крае. Оболочка как бы стремится оттолкнуться от соседней, причём при расчёте по безмоментной теории суммарная горизонтальная сила отпора может оказаться весьма значительной.
Следует оговориться, что вопрос о взаимном «отталкивании» соседних оболочек, имеющих общую диафрагму, нуждается в дополнительном исследовании. Напомним в связи с этим, что безмоментная теория расчёта пологих оболочек двоякой кривизны базируется на трёх основных предположениях: во-первых, равенство нулю изгибающих моментов, а, следовательно, и соответствующих им поперечных усилий по всей поверхности оболочки; во-вторых, контур оболочек абсолютно жёсткий в своей плоскости; в-третьих, контурные элементы не сопротивляются усилиям, направленным нормально их плоскости.
Мы уже останавливались на неточности третьего предположения, особенно в угловых зонах оболочки. Обращаясь к первому предположению о безмоментном напряжённом состоянии оболочки, необходимо отметить, что, как будет показано далее, это предположение вблизи контура не оправдывается.
Вблизи контура возникают существенные краевые изгибающие моменты и соответствующие им поперечные силы; отсюда вытекает, что нагрузка с оболочки на контур передаётся не только через сдвигающие усилия, как это следует из безмоментной теории, но и через поперечные силы, соответствующие моментному состоянию. Значит, безмоментные компоненты напряжённого состояния в действительности меньше вычисленных по безмоментной теории, в том числе меньше нормальные усилия, вызывающие взаимное «отталкивание» на общей диафрагме многоволновых оболочек.
Обратимся, наконец, к рассмотрению второго предположения – об абсолютной жёсткости контурных диафрагм в вертикальной плоскости. Реальные диафрагмы имеют конечную жёсткость. Они прогибаются в вертикальной плоскости, что сопровождается прогибом совместно с ними работающих оболочек. Упругость диафрагм существенно сказывается на напряжённом состоянии оболочки.
В 1962 г. в Ленинграде были проведены экспериментальные исследования на моделях оболочек двоякой кривизны, в ходе которых замерялись деформации свободного края оболочки при абсолютно жёсткой и при упругоподатливой диафрагме. В первом случае контур деформировался наружу по всей длине в соответствии с безмоментной теорией. Во втором случае контур вблизи углов претерпел незначительную деформацию наружу, а в средней части прогнулся внутрь. Изменение знака деформации свидетельствует об изменении знака усилия.
Затем был проделан следующий опыт: один край оболочки закреплялся только от горизонтального смещения; в вертикальном направлении контурный элемент оставался упругоподатливым. При нагружении модели были замерены усилия, возникающие в скорлупе оболочки и направленные нормально к контуру. В полном соответствии с предыдущим экспериментом приборы в средней зоне контура показали растяжение плиты.
По данным ЦНИИСК, также производившего опыты над моделью с упругоподатливым контуром, край оболочки в средней зоне тоже деформировался внутрь – оболочка «сворачивалась». Значить, упругоподатливая диафрагма может изменить не только величину усилия вблизи контура, но даже и его знак.
Правильный учёт влияния податливости диафрагм и совместной работы оболочки с диафрагмой позволит уточнить конкретные усилия; в зависимости от степени податливости диафрагмы усилия взаимодействия двух соседних волн могут изменить знак на обратный.
Выводы:
1. Расчёт тонких оболочек с относительно большим подъёмом при равномерно распределённой нагрузке можно выполнять по безмоментной линейной теории;
2. При расчётах необходимо учитывать условия закрепления оболочки на её контуре, т.е. условия неразрезности;
3. При расчёте отдельно стоящей оболочки по безмоментной теории делается предположение об абсолютной податливости контурных диафрагм в горизонтальном направлении по всей их длине;
4. Диафрагмы, расположенные по внутренним контурам, т.е. общие для двух соседних оболочек, можно приближённо полагать несмещающимися как в своей плоскости, так и из неё. В этом случае нормальные усилия, направленные поперёк оси диафрагмы, не обращаются в нуль. Присоединение оболочки к диафрагме предполагается жёстким;
5. Упругость диафрагм существенно сказывается на напряжённом состоянии оболочки.
Литература:
1.Горенштейн Б.В. Железобетонные пространственные покрытия (Методы разработки и проектирования цилиндрических оболочек, складок и оболочек положительной кривизны). Л., СИ. Ленинградское отделение. 1976, 160 с.
2.Лукаш П.А. Расчет пологих оболочек и плит с учётом физической и геометрической нелинейности. – Сб. «Расчёт конструкций, работающих в упругопластической стадии», М., Госстройиздат, 1961.
3.Руководство по проектированию железобетонных пространственных конструкций покрытий и перекрытий/ НИИЖБ Госстроя СССР. - М.: Стройиздат, 1979. - 421 с.
Annotation. This article presents the calculation of separate and continuous sloping shells of positive curvature according to the momentless theory.
Аннотатсия. Дар мақолаи мазкур ҳисоби гумбазҳои болопӯши алоҳида ва нобуридаи қатшавиашон мусбат мувофиқи назарияи бемоментӣ оварда шудаанд.
Keywords. Gentle shell, continuity, momentless theory, deformation, effort, load, linear theory, nonlinear theory, diaphragm.
Калитвожаҳо. Ҷилди моил, нобурида, назарияи бемоментӣ, шаклдигаркунӣ, қувваҳо, боргузорӣ, назарияи хаттӣ, назарияи ғайрихаттӣ, диафрагма.
Сведения об авторах
1.Нуманов Олим Рахимович – 1955 г.р., выпускник (ТПИ 1977г.) ТТУ, докторант каф. «ПГС», к.т.н., доцент кафедры «Строительство дорог, сооружений и транспортных коммуникаций» ТТУ им. акад. М.С.Осими, автор более 100 науч. работ, область научных интересов - исследование работы неразрезных пространственных конструкций покрытий в сейсмических районах; исследование поведение транспортных сооружений в сейсмических районах. Личные данные: тел.(992) 98-547-15-55, E-mail nor5@mail.ru
2.Набизода Мухаммадтаиби Шариф – соискатель, ст. преп. кафедры «СД, С и ТК» ТТУ им. акад. М.С. Осими, область научной деятельности – пространственные конструкции покрытия, проектирование и строительства дорог. Личные данные: тел.(992) 907-990-300, E-mail nabizoda-90@mail.ru
3.Сангинов Анзор Сатторович – выпускник ТТУ 2015 г., закончил магистратуру в Тюмени РФ в 2017 г., докторант PhD кафедры «СД, С и ТК» ТТУ им. акад. М.С.Осими, область научной деятельности – пространственные конструкции покрытия. Личные данные: тел. (992) 887-786-060.

