Файл: Учебное пособие соответствует рабочей программе дисциплины Строительная механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 80
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. ПРИМЕРЫ ВЫПОЛНЕНИЯ
КИНЕМАТИЧЕСКОГО АНАЛИЗА
ПЛОСКИХ РАСЧЕТНЫХ СХЕМ
П
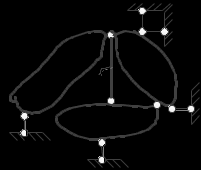 ример 1. Исследовать расчетную схему.
ример 1. Исследовать расчетную схему.1-й этап кинематического анализа
Поскольку РС без замкнутых контуров, то для определения степени свободы используем формулу
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, определяем число дисков: D = 4 (плоские диски: АВ – D1; ВD – D2; KN – D3; прямолинейный стержень: BL – D4).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, Ш = 4 (простые шарниры в точках К и L; двукратные шарниры в точке В; Ш = 1 · 2 + 2 · 1 = 4).
1.3. Число опорных стержней Соп = 5 (шарнирно-подвижные опоры – А, D и М – по одному стержню; шарнирно-неподвижная опора С – два стержня).
1.4. W = 3 · 4 – 2 · 4 – 5 = 12 – 13 = –1.
1.5. Вывод. Заданная РС может быть геометрически неизменяемой, имеет одну избыточную связь, т. е. один раз статически неопределима, так как W = –1.
2-й этап кинематического анализа
2.1. Анализ геометрической структуры РС показывает, что система имеет один диск – D2, с достаточным (не менее трёх) числом связей с диском «земля» (ШПО – D и ШНО – С).
1-й шаг сборки РС. Диск D2 в виде плоского тела ВСD прикрепляется к диску «земля» с помощью трёх линейных связей 1-го типа (ШНО – С – две связи; ШПО – D – одна связь); соединение соответствует типовому правилу 2 (табл. 2.1), причём требование к связям выполняется: оси трёх линейных связей не пересекаются в одной точке и не параллельны; результат сборки – диск D1 = D2 + диск «земля», образованный с помощью только необходимых связей и включающий в себя диск «земля», следовательно, полученная на 1-м шаге сборки система – геометрически неизменяемая и не имеющая избыточных связей.
Сокращенная запись 1-го шага сборки: диск «земля» + D2 = D1 – по правилу 2 (табл. 2.1) образована ГНРС, только с необходимыми связями (соединение двух дисков с помощью трёх связей 1-го типа в форме ШНО – С и ШПО – D; оси связей не пересекаются в одной точке и не параллельны).
2.2. 2-й шаг сборки РС. К геометрически неизменяемой системе –
D1 присоединяется диск D1 с помощью цилиндрического шарнира в точке В и вертикальной линейной связи ШПО – А; соединение соответствует типовому правилу 3 (табл. 2.1), причём требование к связям выполняется: направление оси линейной связи не проходит через шарнир В; результат сборки – диск D2 = D1 + D1, образованный с помощью только необходимых связей и включающий в себя диск «земля», следовательно, полученная на этом шаге сборки система – геометрически неизменяемая и не имеющая избыточных связей.
Сокращенная запись 2-го шага сборки: D2 = D1 + D1 по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями.
2.3. 3-й шаг сборки РС. К геометрически неизменяемой системе – диску D2 – присоединяется диск D3 c помощью цилиндрического шарнира в точке К и двух линейных связей (стержень ВL и опорный стержень ШПО М), что эквивалентно четырём линейным связям, из которых одна избыточная, так как типовые приёмы соединения двух дисков по правилу 3 (табл. 2.1) требуют только трёх связей. в качестве избыточной может рассматриваться, например стержень BL или опорный стержень ШПО М, причём требование к этим связям выполняется: направление осей линейных связей не проходит через шарнир К; результат сборки – диск D3 = D2 + D3 – геометрически неизменяемая система с одной избыточной связью.
Сокращенная запись 3-го шага сборки. D3 = D2 + D3 – по правилу 3 (табл. 2.1) образована ГНРС с одной избыточной (лишней) связью.
3. Окончательный вывод. Заданная РС – геометрически неизменяемая, с простой структурой, с одной лишней связью, т. е. статически неопределимая.
П
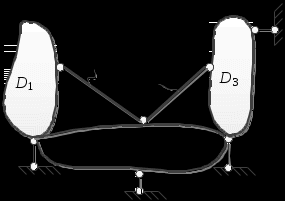 ример 2. Произвести кинематический анализ системы.
ример 2. Произвести кинематический анализ системы. 1-й этап кинематического анализа
Поскольку РС без замкнутых контуров, для определения её степени свободы используем формулу
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, определяем число дисков: D = 5 (плоские тела: АК
– D1; ABC – D2; CD – D3; прямолинейные стержни: KL – D4; LM – D5).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённое к простым, Ш = 6 (простые шарниры в точках А, С, К и М; двукратный шарнир в точке L).
1.3. Число опорных стержней Соп = 4 (в ШПО – А, В, С и D по одному стержню).
1.4. W = 3 · 5 – 2 · 6 – 4 = 15 – 16 = –1.
1.5. Вывод. Заданная РС может быть геометрически неизменяемой, имеет одну избыточную связь, т. е. один раз статически неопределима.
2-й этап кинематического анализа
2.1. 1-й шаг сборки РС: D2 + диск «земля» = D1 – по правилу 2
(табл. 2.1) образована мгновенно изменяемая РС (соединение двух дисков с помощью трёх линейных связей: ШПО – А, В и С, оси которых параллельны друг другу).
На примере рассмотренной РС можно убедиться в необходимости внимательной проверки выполнения требований к расположению связей. Так, если изменить углы наклона осей опорных стержней, то оси не будут параллельны и система будет ГНРС только с необходимыми связями и тогда можно продолжить кинематический анализ.
2.2. 2-й шаг сборки РС: D1 + D1 = D2 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью шарнира в точке А и линейной связи 1-го типа KL; ось связи не проходит через центр шарнира).
2.3. 3-й шаг сборки РС: D2 + D3 = D3 – соединением двух дисков с помощью шарнира в точке С и двумя линейными связями: LM и опорный стержень ШПО D, оси которых не проходят через центр шарнира С, образована ГНРС по правилу 3 (табл. 2.1) с одной избыточной связью.
3. Окончательный вывод. Заданная РС – мгновенно изменяемая.
Если изменить углы наклона осей опорных стержней, то РС будет ГНРС, с простой структурой, с одной лишней связью, т. е. статически неопределимой.
П
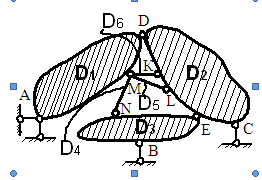 ример 3. Исследовать расчетную схему.
ример 3. Исследовать расчетную схему.





D
К
N
M
L
А
1-й этап кинематического анализа


W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, определяем число дисков: D = 6 (плоские диски АD – D1, DС – D2 и ВЕ – D3; стержни МК – D4, МL – D5 и MN – D6).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым: Ш = 8 (простые шарниры – D, К, L, Е и N; шарнир М – трехкратный (4 – 1 = 3). Итого Ш = 5 · 1 + 1 · 3 = 8).
1.3. Определяем число внешних связей: Соп = 4 (шарнирно-неподвиж-ная опора А – две связи; шарнирно-подвижные опоры В и С – по одной связи. Итого Соп = 1 · 2 + 2 · 1 = 4).
1.4. Определяем степень свободы заданной РС:
W = 3 · 6 – 2 · 8 – 4 = 18 – 20 = –2.
1.5. Вывод. Заданная РСможет быть структурно неизменяемой и дважды статически неопределимой, так как имеет две лишние (избыточные) связи (W = –2).
2-й этап кинематического анализа
2.1. Анализ РСпоказывает, что в системе нет диска с достаточным числом связей с землей, поэтому рассмотрим укрупнение структуры системы путем соединения исходных дисков по типовым правилам.
2.1.1. D5 + D2 + D6 = D1 – по правилу 4 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение трех дисков тремя шарнирами М, L и К; шарниры не лежат на одной прямой).
2.1.2. D1 + D1 = D2 – соединением двух дисков с помощью двух цилиндрических шарниров D и М (эквивалентны четырём простым связям; одна связь – избыточная) образована ГНРС с одной избыточной связью.
2.1.3. D2 + D3 = D3 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью шарнира Е и линейной связи MN; ось связи не проходит через центр шарнира).
2.2. D3 + диск «земля» = D4 – соединением двух дисков с помощью четырех линейных связей; (оси четырёх связей не сходятся в одной точке и не параллельны; одна связь – избыточная) образована ГНРС с одной избыточной связью.
3. Окончательный вывод. заданная расчетная схема геометрически неизменяемая, статически неопределимая, так как имеет две избыточные связи (W = –2)с простой структурой.
П
 ример 4. Произвести кинематический анализ РС.
ример 4. Произвести кинематический анализ РС. 1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РСпо формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что РСсостоит из пяти дисков, т. е. D = 5 (плоские диски АВ – D1, ВС – D2, DЕ – D3; стержни MN – D4, КL – D5).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, Ш = 6 (простые шарниры в точках B, C, K, L, M и N).
1.3. Число опорных стержней Соп = 6 (ШНО А и Е по два стержня, ШПО М и D по одному стержню).
1.4. Определяем степень свободы W = 3 · 5 – 2 · 6 – 6 = 15 – 18 = –3.
1.5. Вывод. Заданная РСможет быть структурно неизменяемой и трижды статически неопределима, так как имеет три лишние связи (W = –3).
2-й этап кинематического анализа: структурный анализ РС.
2.1. Анализ РСпоказывает, что в системе есть два диска с достаточным числом связей с землей – D1 и D3.
2.2. диск «земля» + D1 = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трёх связей 1-го типа, оси которых не пересекаются в одной точке и не параллельны друг другу).
2.3. D1 + D2 = D2 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью шарнира В и линейной связи MN; ось связи не проходит через центр шарнира).
2.4. D2 + D3 = D3 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью шарнира С и линейной связи KL; ось связи не проходит через центр шарнира).
2.5. D3 + «три линейные связи в точках Е и D» – образована ГНРС с тремя избыточными связями.
3. Окончательный вывод. Заданная РСгеометрически неизменяемая, статически неопределимая, так как имеет три избыточные связи (W = –3), с простой структурой.
Пример 5. Исследовать систему.
1-й этап кинематического анализа
Аналитическим методом определим степень свободы РСпо формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что система состоит из четырёх дисков, т. е. D = 4 (АС – D1, СЕ – D2, ЕF – D3 и FH – D3).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 3 (простые шарниры С, Е и F).
1.3. Число опорных стержней Соп = 6 (ШНО – А, четыре ШПО – В, D, G и H).
1.4. Определяем степень свободы W = 3 · 4 – 2 · 3 – 6 = 12 – 12 = 0.
1.5. Вывод. Заданная РСможет быть геометрически неизменяемой и статически определимой (W = 0).
2-й этап кинематического анализа: структурный анализ РС.
2.1. Анализ РСпоказывает, что в системе есть диск с достаточным числом связей с землей – D1.
2.2. диск «земля» + D1 = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трёх связей 1-го типа, оси которых не пересекаются в одной точке и не параллельны друг другу).
2.3. D1 + D2 = D2 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью шарнира С и линейной связи (ШПО – D); ось связи не проходит через центр шарнира).
2.4. D2 + D4 = D3 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трех связей 1-го типа – ЕF, ШПО – G и H; оси которых не параллельны друг другу и не пересекаются в одной точке).
3. Окончательный вывод. Заданная РСгеометрически неизменяемая и статически определимая (W = 0).
П
 ример 6. Произвести кинематический анализ системы.
ример 6. Произвести кинематический анализ системы.1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РСпо формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что РСсостоит из пяти дисков, т. е. D = 5 (стержни АВ – D1, ВD – D2, ВС – D3, АС – D4, СD – D5).
1.2. Отбросив все опорные стержни определяем число шарниров, приведенных к простым, Ш = 6 (простые шарниры в точках А и D, двукратные в точках В и С).
1.3. Число опорных стержней (линейных связей 1-го типа) Соп = 3 (ШНО – А – два стержня; ШПО – D – один стержень).
1.4. Определяем степень свободы
W = 3 · 5 – 2 · 6 – 3 = 15 – 15 = 0.
1.5. Вывод. Заданная РСможет быть структурно неизменяемой и статически определимой (W = 0).
2-й этап кинематического анализа: структурный анализ РС.
2.1. D1 + D3 + D4 = D1 – по правилу 4 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение трех дисков с помощью трёх цилиндрических шарниров; шарниры А, В и С не лежат на одной прямой).
2.2. D1 + D2 = D2 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью шарнира В и линейной связи СD; ось связи не проходит через центр шарнира).
2.3. D2 + диск «земля» = D3 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью тех связей 1-го типа, оси которых не пересекаются в одной точке и не параллельны друг другу).
3. Окончательный вывод. Заданная РСгеометрически неизменяема и статически определима, с простой структурой.
П
 ример 7. Исследовать расчетную схему.
ример 7. Исследовать расчетную схему. 1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РСпо формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что РСсостоит из двух дисков, т.е. D = 2 (ломаный стержень АВСК – D1, прямолинейный стержень СD – D2).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, Ш = 2 (простые шарниры в точках В и С).
1.3. Число опорных стержней Соп = 6 (ШНО А, D и К – по два стержня).
1.4. Определяем степень свободы РС:W = 3 · 2 – 2 · 2 – 6 = 6 – 10 = –4.
1.5. Вывод. Заданная РСможет быть структурно неизменяемой и четырежды статически неопределима, так как имеет четыре избыточных связи.
2-й этап кинематического анализа: структурный анализ РС.
2.1. диск «земля» + D1 = D1 – по правилу 2 (табл. 2.1) образована ГНРС с одной избыточной связью (горизонтальный стержень в ШНО А или К, соединение двух дисков с помощью трёх связей 1-го типа, оси которых не пересекаются в одной точке и не параллельны друг другу).
2.2. D1 + D2 = D2 – по правилу 3 (табл. 2.1) образована ГНРС с одной избыточной связью (вертикальный опорный стержень ШНО D, соединение двух дисков с помощью шарнира С и горизонтального опорного стержня ШНО D; ось опорного стержня не проходит через центр шарнира).
2.3. Простой шарнир В, эквивалентный двум связям 1-го типа, лишний, так как и без него РСнеизменяема.
3. Окончательный вывод. заданная РСгеометрически неизменяемая, трижды статически неопределимая (W = –3), с простой структурой.
П
 ример 8. Произвести кинематический анализ расчетной схемы.
ример 8. Произвести кинематический анализ расчетной схемы. 1-й этап кинематического анализа
Аналитическим методом определяем степень свободы
W = 3 · 4 – 2 · 5 – 6 = 12 – 16 = –4.
1.1. Вывод. заданная РСможет быть структурно неизменяемой и четырежды статически неопределима, так как имеет четыре избыточные связи (W = –4).
2-й этап кинематического анализа: структурный анализ РС.
2.1. Анализ расчетной схемы позволяет сделать вывод, что есть два диска D1 – ANOB и D2 – BPRC, которые соединены с землей достаточным (не менее трёх) числом связей. Начнем сборку системы с D1.
2.2. D1 + диск «земля» = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трёх связей 1-го типа (ШНО А и ШПО В), оси которых не пересекаются в одной точке и не параллельны друг другу).
2.3. D1 + D2 = D2 – по правилу 3 (табл. 2.1) образована ГНРС с двумя избыточными связями (соединение двух дисков с помощью шарнира В и жесткой заделки С, что эквивалентно пяти линейным связям 1-го типа; для образования неизменяемой системы достаточно трёх связей).
2.4. Стержни DK и LM – избыточные, так как и без этих связей исследованная система геометрически неизменяема и неподвижна.
3. Окончательный вывод. Заданная РСгеометрически неизменяемая, четырежды статически неопределима (W = –4), с простой структурой.
П
 ример 9. Произвести кинематический анализ системы.
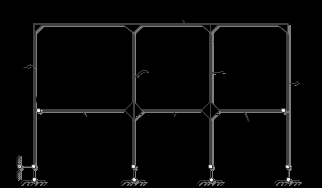
ример 9. Произвести кинематический анализ системы. 1-й этап кинематического анализа
Аналитическим методом определяем степень свободы. Поскольку система имеет замкнутый контур EFIK, то для определения её степени свободы используем универсальную формулу
W = 3D – 3П – 2Ш – С – Соп.
1.1. В качестве дисков примем стержни AB – D1, BC – D2, CD – D3,
GI – D4, IK – D5, KH – D6, EL – D7, FM – D8 (стержни EL и FM приняты сплошными), т.е. D = 8.
1.2. Шарниры G и H – простые. Ш = 2.
1.3. Жесткие узлы (припайки) B, E, F и C простые, каждый из жестких узлов (припаек) I и К – двукратный, так как соединяет по три стержня (к стержню ЕL в узле I жестко присоединены стержни GI и KI, а к стержню FM в узле К – стержни IK и HK); суммарное число жестких прикреплений (припаек)
П = 1 · 4 + 2 · 2 = 8.
1.4. Число опорных стержней Соп = 5 (ШНО А – две связи 1-го типа, ШПО L, M и D – три связи 1-го типа).
1.5. Число внутренних связей 1-го типа С = 0.
1.6. Степень свободы системы
W = 3 · 8 – 3 · 8 – 2 · 2 – 0 – 5 = 24 – 33 = –9.
1.7. Вывод. Заданная система может быть неизменяемой и имеет девять избыточных связей.
2-й этап кинематического анализа: структурный анализ РС.
2.1. Анализ геометрической структуры показывает, что внешний контур ABCD представляет укрупненный супердиск D1.
2.2. D1 + диск «земля» = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трёх связей 1-го типа (ШНО А – две связи, ШПО D – одна связь).
2.3. D1 + укрупненный супердиск CEFIKHLM = D2 (соединение двух дисков шарнирами G и H (четыре связи), припайками Е и F (шесть связей), двумя опорными стержнями (ШПО L и М). В общей сложности
укрупненный супердиск прикреплен к первому диску D1 двенадцатью связями, а для геометрической неизменяемости и неподвижности его достаточно трёх связей, следовательно, девять связей с точки зрения неизменяемости являются лишними.
3. Окончательный вывод. в результате произведённого кинематического анализа заключаем, что рассмотренная РСнеизменяема, неподвижна, девять раз статически неопределима (W = –9) и с простой структурой.
П
 ример 10. Произвести кинематический анализ системы.
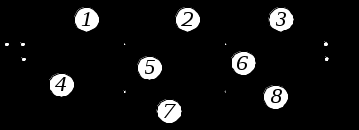
ример 10. Произвести кинематический анализ системы.1-й этап кинематического анализа
Аналитическим методом определяем степень свободы системы. Поскольку РСявляется шарнирно-стержневой (фермой), для определения её степени свободы используем формулу
W = 2У – Сф – Соп.
1.1. Определяем число узлов системы У = 6.
1.2. Число стержней фермы Сф = 8.
1.3. Число опорных стержней Соп = 3.
1.4. Степень свободы
W = 2 · 6 – 8 – 3 = 12 – 11 = 1.
1.4. Вывод. Заданная РСимеет одну степень свободы, т. е. является механизмом и не может быть использована в качестве строительной конструкции.
П
 ример 11. Исследовать систему.
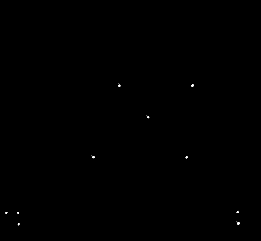
ример 11. Исследовать систему.1-й этап кинематического анализа
Аналитическим методом определяем степень свободы по формуле
W = 2У – Сф – Соп.
1.1. Число узлов У = 7.
1.2. Число стержней фермы Сф = 11.
1.3. Число опорных стержней Соп = 3.
1.4. W = 2 · 7 – 11 – 3 = 14 – 14 = 0.
1.5. Вывод: система имеет необходимое количество связей, чтобы быть неизменяемой и статически определимой (W = 0).
2-й этап кинематического анализа: структурный анализ РС.
2.1. Диск D1 (стержень АВ) + диск «земля» = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трех связей 1-го типа (ШНО А и ШПО В), оси которых не пересекаются в одной точке и не параллельны друг другу).
2.2. D1 + супердиск D2 (неизменяемый треугольник СDЕ) + супердиск D3 (неизменяемый треугольник EFG) = D2 – по правилу 5 (табл. 2.1) (три диска попарно соединены с помощью трёх пар линейных связей – D1 c D2 – двумя стержнями АС и ВD; D1 с D3 – двумя стержнями АF и ВG; D2 с D3 – шарниром в точке Е). Шарнир Е является мгновенным центром вращения дисков D2 и D3, а также дисков D1 и D2 , так как здесь находится фиктивный шарнир, заменяющий стержни АС и ВD, соединяющие эти два диска. Следовательно, система мгновенно изменяемая, так как где бы ни находился мгновенный центр О вращения дисков D1 и D3, через него и точку Е можно всегда провести прямую, на которой будут лежать все три мгновенных центра вращения.
3. Окончательный вывод. заданная система – мгновенно изменяемая.
П
 ример 12. Исследовать систему.
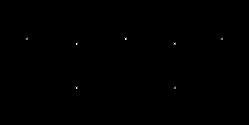
ример 12. Исследовать систему.1-й этап кинематического анализа
Аналитическим методом определяем степень изменяемости системы по формуле
V = 3D – 2Ш – 3.
1.1. Отбросив все шарниры, находим, что РС состоит из семи дисков, т. е. D = 7 (стержни АВС – D1; СDE – D2; AK – D3; BK – D4; KL – D5; DL – D6; EL – D7).
1.2. Число шарниров, приведенных к простым, Ш = 9 (простые шарниры – А, В, С, D и Е; двукратные шарниры – К и L; Ш = 1 · 5 + 2 · 2 = 9).
1.3. V = 3 · 7 – 2 · 9 – 3 = 21 – 21 = 0.
1.4. Вывод. Заданная РСимеет необходимое количество связей, чтобы быть неизменяемой и статически определимой.
2-й этап кинематического анализа: структурный анализ РС.
2.1. D1 + D3 + D4 = D1 – по правилу 4 (табл. 2.1) образована ГНРС только с необходимыми связями (три диска соединены с помощью трёх шарниров А, В и К; которые не лежат на одной прямой).
2.2. D2 + D6 + D7 = D2 – по правилу 4 (табл. 2.1) образована ГНРС только с необходимыми связями.
2.3. D1 + D2 = D3 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (два диска соединены с помощью шарнира С и линейной связи КL; ось связи не проходит через центр шарнира).
3. Окончательный вывод. Заданная РСгеометрически неизменяема, неподвижна и статически определима.
П
 ример 13. Произвести кинематический анализ РС.
ример 13. Произвести кинематический анализ РС. 1-й этап кинематического анализа
Аналитическим методом определяем степень изменяемости РСпо формуле
V = 2У – Сф – 3.
1.1. Число узлов в ферме У = 6.
1.2. Число стержней фермы Сф = 8.
1.3. V = 2 · 6 – 8 – 3 = 12 – 11 = 1.
1.4. Вывод. Заданная РСимеет одну степень свободы, т. е. является механизмом и не может быть использована в качестве строительной конструкции.
П
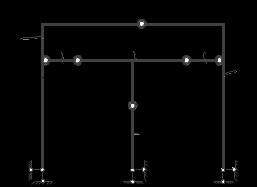 ример 14. Исследовать систему.
ример 14. Исследовать систему. 1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РС по формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что РСсостоит из шести дисков, т. е. D = 6 (стержни АВС – D1, СDE – D2, FG – D3, GIL – D4, IK – D5,
LM – D6).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 6 (простые шарниры C, F, G, I, K, L).
1.3. Число опорных стержней (связей 1-го типа) Соп = 6 (ШНО А, М и Е).
1.4. W = 3 · 6 – 2 · 6 – 6 = 18 – 18 = 0.
1.5. Вывод. Заданная РСможет быть структурно неизменяемой и статически определимой.
2-й этап кинематического анализа: структурный анализ РС.
2.1. D1 + D2 + диск «земля» = D1 – по правилу 4 (табл. 2.1) образована ГНРС (три диска соединены с помощью трёх цилиндрических шарниров, которые не лежат на одной прямой).
2.2. D1 + D4 = D2 – по правилу 2 (табл. 2.1) образована МИРС (два диска соединены при помощи трех линейных связей – стержней FG, IK и LM; оси которых пересекаются в одной точке H, являющейся мгновенным центром вращения).
3. Окончательный вывод: заданная РСмгновенно изменяемая.
П
 ример 15. Произвести кинематический анализ системы.
ример 15. Произвести кинематический анализ системы. 1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РСпо формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что РС состоит из четырёх дисков, т. е. D = 4 (плоские диски АК – D1 и ВL – D2; стержни CD – D3, KL – D4).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 4 (простые шарниры C, D, K, L).
1.3. Число опорных стержней Соп = 4 (ШНО А и В).
1.4. W = 3 · 4 – 2 · 4 – 4 = 12 – 12 = 0.
1.5. Вывод. РС может быть структурно неизменяемой и статически
определимой.
2-й этап кинематического анализа: структурный анализ РС.
2.1. D1 + D2 + диск «земля» = D1 – по правилу 5 (табл. 2.1) образована ГНРС только с необходимыми связями (три диска соединены попарно с помощью трёх пар линейных связей – ШНО А, В и стержни СD, KL; точки пересечения каждой пары линейных связей не лежат на одной прямой и линейные связи не параллельны между собой).
3. Окончательный вывод: заданная РС геометрически неизменяемая и статически определимая.
П
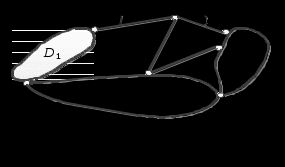 ример 16. Исследовать систему.
ример 16. Исследовать систему.1-й этап кинематического анализа
Аналитическим методом определяем степень изменяемости РС по формуле
V = 3D – 2Ш – 3.
1.1. Отбросив все шарниры и опорные стержни, находим, что система состоит из семи дисков, т. е. D = 7 (плоские диски АК – D1, AB – D2, BN – D3; стержни KL – D4, LN – D5, CL – D6, CD – D7).
1.2. Отбросив все опорные связи, определяем число шарниров, приведённых к простым, Ш = 9 (простые шарниры А, В, К, D, N; двукратные шарниры L и С; Ш = 1 · 5 + 2 · 2 = 9).
1.3. V = 3 · 7 – 2 · 9 – 3 = 21 – 21 = 0.
1.4. Вывод. Заданная РС может быть структурно неизменяемой и статически определимой.
2-й этап кинематического анализа: структурный анализ РС.
2.1. D2 + D3 + D7 = D1 – по правилу 4 (табл. 2.1) образована ГНРС только с необходимыми связями (три диска соединены с помощью трёх цилиндрических шарниров, которые не лежат на одной прямой).
2.2. D1 + узел L = D2 – по правилу 1 (табл. 2.1) образована ГНРС только с необходимыми связями (узел L прикреплен к неизменяемому диску D1 двумя линейными связями, не лежащими на одной прямой).
2.3. D2 + D1 = D3 – по правилу 3 (табл. 2.1) образована ГНРС только с необходимыми связями (два диска соединены с помощью шарнира А и линейной связи КL; продольная ось которой не проходит через центр шарнира).
3. Окончательный вывод. Заданная РС геометрически неизменяемая и статически определима.
П
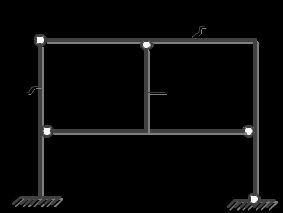 ример 17. Произвести кинематический анализ системы.
ример 17. Произвести кинематический анализ системы.1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РС по формуле
W = 3D – 2Ш – Соп.
1.1. Отбросив все шарниры и опорные стержни, находим, что РС состоит из трех дисков, т. е. D = 3 (стержни АС – D1, CDKL – D2, BDK – D3).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 4 (простые шарниры в точках В, С, К, D).
1.3. Число опорных стержней Соп = 5 (ЖЗ А – три стержня; ШНО L – два стержня).
1.4. W = 3 · 3 – 2 · 4 – 5 = 9 – 13 = –4.
1.5. Вывод. Заданная РС может быть структурно неизменяемой и четырежды статически неопределимой, т. е. имеет четыре избыточных связи.
2-й этап кинематического анализа: структурный анализ РС.
2.1. D1 + диск «земля» = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (два диска соединены при помощи трёх линейных связей (стержней) – ЖЗ А).
2.2. D1 + D2 = D2 – образована ГНРС с одной избыточной связью соединением двух дисков с помощью двух цилиндрических шарниров (четырёх эквивалентных простых связей; одна связь – избыточная).
2.3. D2 + D3 = D3 – образована ГНРС с тремя избыточными связями (соединение двух дисков с помощью трёх цилиндрических шарниров (шесть эквивалентных простых связей; три связи – избыточные)).
3. Окончательный вывод. заданная РС геометрически неизменяемая, с простой структурой, с четырьмя избыточными (лишними) связями,
т. е. статически неопределимая.
Пример 18. Исследовать систему.
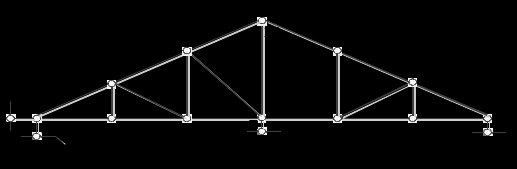
1-й этап кинематического анализа
Поскольку РС является шарнирно-стержневой, для определения её степени свободы используем формулу
W = 2У – Сф – Соп.
1.1. Число узлов системы У = 12.
1.2. Число стержней фермы Сф = 20.
1.3. Число опорных стержней Соп = 4.
1.4. W = 2 · 12 – 20 – 4 = 24 – 24 = 0.
1.5. Вывод. Необходимое условие геометрической неизменяемости соблюдено, следовательно, РС может быть неизменяемой и статически опре-делимой (W = 0).
2-й этап кинематического анализа: структурный анализ РС.
2.1. Производя структурный анализ, нетрудно доказать неизменяемость двух частей системы АВС – D1 и ВСD – D2, состоящих из простых шарнирных треугольников (триад).
2.2. D1 + диск «земля» = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков с помощью трёх связей 1-го типа в форме ШНО – А и ШПО – В).
2.3. D1 + D2 = D2 – по правилу 2 (табл. 2.1) образована МИРС (два диска соединены при помощи трёх линейных связей 10–11, 4–5 и опорного стержня ШПО – D, оси которых пересекаются в одной точке D, являющейся мгновенным центром вращения).
3. Окончательный вывод. Заданная РС является мгновенно изменяемой.
П
 ример 19. Произвести кинематический анализ системы.
ример 19. Произвести кинематический анализ системы.1-й этап кинематического анализа
Аналитическим методом определяем степень свободы РС по формуле
W = 3D – 2Ш – Соп.
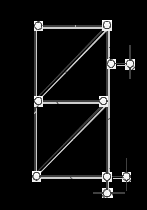
1.1. Отбросив все шарниры и опорные стержни, находим, что РС состоит из семи дисков, т. е. D = 7 (стержни BL – D1, AM – D2, AB – D3, CD – D4, LM – D5, BC – D6, DM – D7).
1.2. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 10 (простые шарниры – L и А; двукратные шарниры – В, С, D, М; Ш = 1 · 2 + 2 · 4 = 10).
1.3. Число опорных стержней Соп = 3.
1.4. W = 3 · 7 – 2 · 10 – 3 = 21 – 23 = –2.
1.5. Вывод. Заданная РС может быть структурно неизменяемой и два раза статически неопределимой.
2-й этап кинематического анализа: структурный анализ РС.
2.1. D2 + диск «земля» = D1 – по правилу 2 (табл. 2.1) образована ГНРС только с необходимыми связями (соединение двух дисков при помощи трех связей 1-го типа – ШНО А, ШПО К, оси которых не пересекаются в одной точке и не параллельны друг другу).
2.2. «Узел В» + D1 = D2 – по правилу 1 (табл. 2.1) образована ГНРС только с необходимыми связями (узел прикреплён к неизменяемому диску двумя линейными связями ВС и АВ, не лежащими на одной прямой).
2.3. «Узел D» + D2 = D3 – по правилу 1 (табл. 2.1) образована ГНРС только с необходимыми связями.
2.4. Диски ВL и LM – избыточные связи.
3. Окончательный вывод. Заданная РС геометрически неизменяемая, с простой структурой с двумя лишними связями, т.е. статически неопределимая.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ [4]
1. Кинематический анализ систем
Выполнить кинематический анализ для приведенных ниже систем.
1.1 1.2




1.6
1.5
1.4
1.3
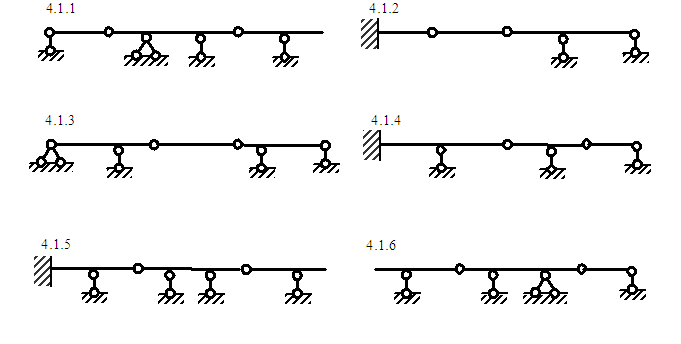
1.7 1.8

1.9 1.10

1.11 1.12

1.13 1.14

1.15 1.16




1.20
1.19
1.18
1.17
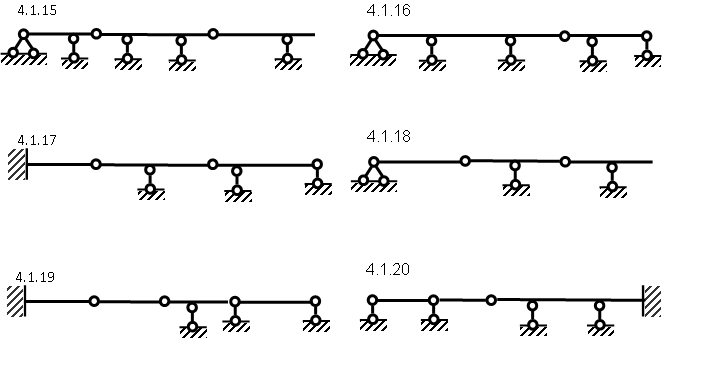
1.21 1.22
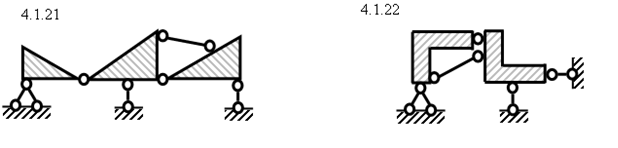


1.24
1.23

1.25 1.26


1.28
1.27

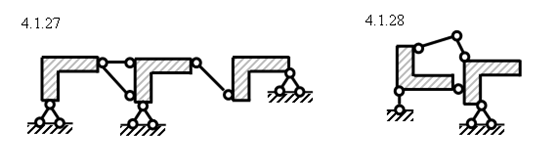
1.29 1.30

1.31 1.32


