Файл: Учебное пособие соответствует рабочей программе дисциплины Строительная механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 86
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
П – 2Ш – С – 3.
1.2. Если заданная РС не имеет замкнутых контуров без шарниров (рис. 2.1, б), то степень свободы (изменяемости) определяем по формулам:
W = 3D – 2Ш – С – Соп;
V = 3D – 2Ш – С – 3.


б
а

Рис. 2.1. Расчетные схемы
Если считать внутренние связи 1-го типа за диски, получим
W = 3D – 2Ш – Соп;
V = 3D – 2Ш – 3.
1.3. Если заданная РС является шарнирно-стержневой, то степень свободы (изменяемости) определяем по формулам:
W = 2У – Сф – Соп;
V = 2У – Сф – 3.
2. Проводим анализ геометрической структуры РСсооружения и определяем, какие элементы будем считать дисками, а какие рассматривать как связи. При этом необходимо строго учитывать, что один и тот же элемент РСне может одновременно быть и диском, и связью; связи должны налагаться только на диски, а не друг на друга.
При разделении РСна диски и связи не должно остаться ни одного элемента, не отнесенного к одной или другой категории.
3. Отбросив все припайки, шарниры и опорные стержни, определяем число дисков, из которых состоит система, D (без учёта диска «земля»).
4. Определяем возможные комбинации соединения дисков друг с другом, исключив диск «земля».
5. Каждую комбинацию проверяем на предмет реального существования возможных соединений соответствующих дисков, и в случае наличия связей (одной или нескольких) определяем их типы.

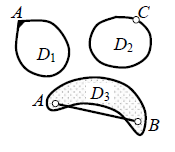
Рис. 2.2. Проверка наличия связей между точками одного и того же диска
6. Дополнительно для всех дисков проверяем наличие связей между точками одного и того же диска (примеры: связь 3-го типа (припайка) в узле
А диска D1 (криволинейного стержня с замкнутой осью), связь
2-го типа (простой шарнир) в диске – стержня D2 и связь АВ 1-го типа (линейная) в диске D3) [3] (рис. 2.2).
7. Отбросив все шарниры и опорные стержни, определяем число припаек, приведенное к простым, – П.
8. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, – Ш.
9. Определяем число внутренних связей 1-го типа – С.
10. Во всех точках, где имеются соединения с диском «земля» (опоры), т. е. внешние связи, оцениваются их типы и подсчитывается число эквивалентных им связей 1-го типа – определяется число внешних связей – Соп.
10.1. Шарнирно-подвижная опора (ШПО) Соп = 1;
10.2. Шарнирно-неподвижная опора (ШНО) Соп = 2;
10.3. Жесткая заделка (ЖЗ) Соп = 3.
11. Определяем степень свободы (изменяемости) заданной системы.
12. Делаем предварительный вывод.
12.1. РС может быть геометрически неизменяемой (если W(V) = 0 или W(V) < 0;
12.2. РС геометрически изменяемая (при W(V) > 0).

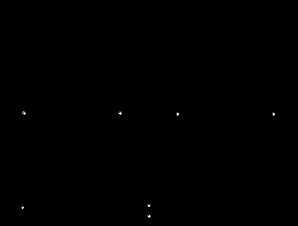
Рис. 2.3. Заданная расчетная схема сооружения
Рассмотрим пример реализации выше приведенного алгоритма для РС, приведенной на рис. 2.3.
При этом рассмотрим несколько возможных вариантов представления о её дисках и связях.
1-й вариант. Определяем степень свободы заданной РС по универсальной формуле (2.1).
Решение
1. Определяем, какие элементы РСбудем считать дисками, а какие – связями.
1.1. Дисками будем считать стержни: АN – D1; NО – D2; РR – D3; ОВ – D4; ВР – D5; RC – D6.
1.2. Внешние связи: шарнирно-неподвижная опора (ШНО) А; шарнирно-подвижная опора (ШПО) В; жесткая заделка (ЖЗ) С.
1.3. Внутренние связи: стержни DК и LM – связи 1-го типа; простые припайки в жестких узлах N, O, P и R; простой шарнир в шарнирном узле В.
2. Отбросив все припайки, шарниры и опорные стержни, находим, что РС состоит из шести дисков, т.е. D = 6.
3. Отбросив все шарниры и опорные стержни, определяем число припаек, приведенных к простым,
П = 4 (простые припайки N, O, P и R).
4. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 1 (простой шарнир В).
5. Определяем число внутренних связей 1-го типа: С = 2.
6. Определяем число внешних связей, эквивалентных связям 1-го типа: Соп = 6.
7. Определяем степень свободы заданной РСпо формуле (2.1)
W = 3 · 6 – 3 · 4 – 2 · 1 – 2 – 6 = 18 – 22 = –4.
8. Вывод. Заданная РС может быть геометрически неизменяемой и четырежды статически неопределимой, так как W = –4.
2-й вариант. Определяем степень свободы заданной РСпо формуле (2.2).
Решение
1. Определяем, какие элементы РСбудем считать дисками, а какие – связями.
1.1. Дисками будем считать: АNOB – D1; ВРRC – D2.
1.2. Внешние связи: ШНО – А; ШПО – В; ЖЗ – С.
1.3. Внутренние связи: стержни DK и LR – связи 1-го типа; простой цилиндрический шарнир в точке В; простых припаек нет.
2. Отбросив все шарниры и опорные стержни, находим, что РС состоит из двух дисков, т. е. D = 2.
3. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, Ш = 1.
4. Определяем число внутренних связей 1-го типа: С = 2.
5. Определяем число внешних связей, эквивалентных связям 1-го типа: Соп = 6.
6. Определяем степень свободы заданной РСпо формуле (2.2)
W = 3 · 2 – 2 · 1 – 2 – 6 = 6 – 10 = –4.
7. Вывод. Заданная РС может быть геометрически неизменяемой и четырежды статически неопределимой, так как W = –4.
3-й вариант. Определим степень свободы заданной РС по формуле (2.3).
Решение
1. Определяем, какие элементы РСбудем считать дисками, а какие – связями.
1.1. Дисками будем считать: АNOB – D1; BPRC – D2; DK – D3; LM – D4.
1.2. Внешние связи: ШНО – А; ШПО – В; ЖЗ – С.
1.3. Внутренние связи: связей 1-го типа нет; простых припаек нет; простые шарниры – узлы D, К, В, L, М и В.
2. Отбросив все шарниры и опорные стержни, находим, что РС состоит из четырёх дисков, т. е. D = 4.
3. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 5.
4. Определяем число внешних связей, эквивалентных связям 1-го типа, Соп = 6.
5. Определяем степень свободы заданной РС по формуле (2.3)
W = 3 · 4 – 2 · 5 – 6 = 12 – 16 = –4.
Во всех вариантах получено, как и следовало ожидать, одно и то же значение W = –4 < 0. Заключение по результатам 1-го этапа кинематического анализа: заданная расчетная схема может быть геометрически неизменяемой, так как связей количественно хватает (и даже имеется четыре избыточных), чтобы при правильном их размещении обеспечить устранение всех степеней свободы дисков РС.
Как уже отмечалось выше, если в результате выполнения 1-го этапа кинематического анализа обнаружено, что РСсооружения удовлетворяет необходимому аналитическому условию геометрической неизменяемости, то осуществляется её качественный (структурный) анализ, представляющий 2-й этап кинематического анализа.
Структурный анализ РСсводится к воспроизведению последовательности операций по образованию (сборке) системы из исходного набора несвязанных дисков наложением связей, предусмотренных расчетной схемой. При этом каждый шаг сборки РСзаключается в соединении нескольких дисков (исходных или созданных путем укрупнения – супердисков) с помощью определенных комбинаций связей. Результатом очередного шага сборки должно быть либо получение геометрически неизменяемой части системы (если это возможно обеспечить набором связей, имеющихся в РС), либо выявление дефектов в расположении связей.
В большинстве случаев разные ситуации в процессе сборки системы могут быть сведены к применению типовых правил геометрически неизменяемого соединения элементов (дисков), изложенных в п. 2.3.1 применительно к плоским расчетным схемам.
Структурный анализ можно проводить либо на основе рассмотрения последовательного образования (монтажа), либо последовательного демонтажа системы. Отметим, что если при демонтаже какой-либо части РСоставшаяся часть остаётся неизменяемой, то удаленная часть называется дополнительной (по отношению к оставшейся), а оставшаяся – главной частью РС.
В ходе структурного анализа дается оценка кинематического качества каждой внешней и внутренней связи на основании кинематического признака классификации связей. По этому признаку классифицируются только простые (линейные и угловые) связи, которые подразделяются на необходимые, лишние и ложные. Имеющиеся в РС сложные связи (шарниры, припайки) предварительно представляются как соответствующие комбинации простых связей.
Типовые правила (табл. 2.1) различаются набором соединяемых объектов (в порядке усложнения: «диск и точка», «два диска», «три диска», причем точка формально может рассматриваться как диск бесконечно малых размеров); связи – только необходимые [3].
Таблица 2.1
Типовые правила геометрически неизменяемого соединения элементов
1.2. Если заданная РС не имеет замкнутых контуров без шарниров (рис. 2.1, б), то степень свободы (изменяемости) определяем по формулам:
W = 3D – 2Ш – С – Соп;
V = 3D – 2Ш – С – 3.


б
а

Рис. 2.1. Расчетные схемы
Если считать внутренние связи 1-го типа за диски, получим
W = 3D – 2Ш – Соп;
V = 3D – 2Ш – 3.
1.3. Если заданная РС является шарнирно-стержневой, то степень свободы (изменяемости) определяем по формулам:
W = 2У – Сф – Соп;
V = 2У – Сф – 3.
2. Проводим анализ геометрической структуры РСсооружения и определяем, какие элементы будем считать дисками, а какие рассматривать как связи. При этом необходимо строго учитывать, что один и тот же элемент РСне может одновременно быть и диском, и связью; связи должны налагаться только на диски, а не друг на друга.
При разделении РСна диски и связи не должно остаться ни одного элемента, не отнесенного к одной или другой категории.
3. Отбросив все припайки, шарниры и опорные стержни, определяем число дисков, из которых состоит система, D (без учёта диска «земля»).
4. Определяем возможные комбинации соединения дисков друг с другом, исключив диск «земля».
5. Каждую комбинацию проверяем на предмет реального существования возможных соединений соответствующих дисков, и в случае наличия связей (одной или нескольких) определяем их типы.


Рис. 2.2. Проверка наличия связей между точками одного и того же диска
6. Дополнительно для всех дисков проверяем наличие связей между точками одного и того же диска (примеры: связь 3-го типа (припайка) в узле
А диска D1 (криволинейного стержня с замкнутой осью), связь
2-го типа (простой шарнир) в диске – стержня D2 и связь АВ 1-го типа (линейная) в диске D3) [3] (рис. 2.2).
7. Отбросив все шарниры и опорные стержни, определяем число припаек, приведенное к простым, – П.
8. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, – Ш.
9. Определяем число внутренних связей 1-го типа – С.
10. Во всех точках, где имеются соединения с диском «земля» (опоры), т. е. внешние связи, оцениваются их типы и подсчитывается число эквивалентных им связей 1-го типа – определяется число внешних связей – Соп.
10.1. Шарнирно-подвижная опора (ШПО) Соп = 1;
10.2. Шарнирно-неподвижная опора (ШНО) Соп = 2;
10.3. Жесткая заделка (ЖЗ) Соп = 3.
11. Определяем степень свободы (изменяемости) заданной системы.
12. Делаем предварительный вывод.
12.1. РС может быть геометрически неизменяемой (если W(V) = 0 или W(V) < 0;
12.2. РС геометрически изменяемая (при W(V) > 0).


Рис. 2.3. Заданная расчетная схема сооружения
Рассмотрим пример реализации выше приведенного алгоритма для РС, приведенной на рис. 2.3.
При этом рассмотрим несколько возможных вариантов представления о её дисках и связях.
1-й вариант. Определяем степень свободы заданной РС по универсальной формуле (2.1).
Решение
1. Определяем, какие элементы РСбудем считать дисками, а какие – связями.
1.1. Дисками будем считать стержни: АN – D1; NО – D2; РR – D3; ОВ – D4; ВР – D5; RC – D6.
1.2. Внешние связи: шарнирно-неподвижная опора (ШНО) А; шарнирно-подвижная опора (ШПО) В; жесткая заделка (ЖЗ) С.
1.3. Внутренние связи: стержни DК и LM – связи 1-го типа; простые припайки в жестких узлах N, O, P и R; простой шарнир в шарнирном узле В.
2. Отбросив все припайки, шарниры и опорные стержни, находим, что РС состоит из шести дисков, т.е. D = 6.
3. Отбросив все шарниры и опорные стержни, определяем число припаек, приведенных к простым,
П = 4 (простые припайки N, O, P и R).
4. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 1 (простой шарнир В).
5. Определяем число внутренних связей 1-го типа: С = 2.
6. Определяем число внешних связей, эквивалентных связям 1-го типа: Соп = 6.
7. Определяем степень свободы заданной РСпо формуле (2.1)
W = 3 · 6 – 3 · 4 – 2 · 1 – 2 – 6 = 18 – 22 = –4.
8. Вывод. Заданная РС может быть геометрически неизменяемой и четырежды статически неопределимой, так как W = –4.
2-й вариант. Определяем степень свободы заданной РСпо формуле (2.2).
Решение
1. Определяем, какие элементы РСбудем считать дисками, а какие – связями.
1.1. Дисками будем считать: АNOB – D1; ВРRC – D2.
1.2. Внешние связи: ШНО – А; ШПО – В; ЖЗ – С.
1.3. Внутренние связи: стержни DK и LR – связи 1-го типа; простой цилиндрический шарнир в точке В; простых припаек нет.
2. Отбросив все шарниры и опорные стержни, находим, что РС состоит из двух дисков, т. е. D = 2.
3. Отбросив все опорные стержни, определяем число шарниров, приведенных к простым, Ш = 1.
4. Определяем число внутренних связей 1-го типа: С = 2.
5. Определяем число внешних связей, эквивалентных связям 1-го типа: Соп = 6.
6. Определяем степень свободы заданной РСпо формуле (2.2)
W = 3 · 2 – 2 · 1 – 2 – 6 = 6 – 10 = –4.
7. Вывод. Заданная РС может быть геометрически неизменяемой и четырежды статически неопределимой, так как W = –4.
3-й вариант. Определим степень свободы заданной РС по формуле (2.3).
Решение
1. Определяем, какие элементы РСбудем считать дисками, а какие – связями.
1.1. Дисками будем считать: АNOB – D1; BPRC – D2; DK – D3; LM – D4.
1.2. Внешние связи: ШНО – А; ШПО – В; ЖЗ – С.
1.3. Внутренние связи: связей 1-го типа нет; простых припаек нет; простые шарниры – узлы D, К, В, L, М и В.
2. Отбросив все шарниры и опорные стержни, находим, что РС состоит из четырёх дисков, т. е. D = 4.
3. Отбросив все опорные стержни, определяем число шарниров, приведённых к простым, Ш = 5.
4. Определяем число внешних связей, эквивалентных связям 1-го типа, Соп = 6.
5. Определяем степень свободы заданной РС по формуле (2.3)
W = 3 · 4 – 2 · 5 – 6 = 12 – 16 = –4.
-
Вывод. Заданная РС может быть геометрически неизменяемой и четырежды статически неопределимой, так как W = –4.
Во всех вариантах получено, как и следовало ожидать, одно и то же значение W = –4 < 0. Заключение по результатам 1-го этапа кинематического анализа: заданная расчетная схема может быть геометрически неизменяемой, так как связей количественно хватает (и даже имеется четыре избыточных), чтобы при правильном их размещении обеспечить устранение всех степеней свободы дисков РС.
Как уже отмечалось выше, если в результате выполнения 1-го этапа кинематического анализа обнаружено, что РСсооружения удовлетворяет необходимому аналитическому условию геометрической неизменяемости, то осуществляется её качественный (структурный) анализ, представляющий 2-й этап кинематического анализа.
2.3. Структурный анализ расчетных схем сооружений
Структурный анализ РСсводится к воспроизведению последовательности операций по образованию (сборке) системы из исходного набора несвязанных дисков наложением связей, предусмотренных расчетной схемой. При этом каждый шаг сборки РСзаключается в соединении нескольких дисков (исходных или созданных путем укрупнения – супердисков) с помощью определенных комбинаций связей. Результатом очередного шага сборки должно быть либо получение геометрически неизменяемой части системы (если это возможно обеспечить набором связей, имеющихся в РС), либо выявление дефектов в расположении связей.
В большинстве случаев разные ситуации в процессе сборки системы могут быть сведены к применению типовых правил геометрически неизменяемого соединения элементов (дисков), изложенных в п. 2.3.1 применительно к плоским расчетным схемам.
Структурный анализ можно проводить либо на основе рассмотрения последовательного образования (монтажа), либо последовательного демонтажа системы. Отметим, что если при демонтаже какой-либо части РСоставшаяся часть остаётся неизменяемой, то удаленная часть называется дополнительной (по отношению к оставшейся), а оставшаяся – главной частью РС.
В ходе структурного анализа дается оценка кинематического качества каждой внешней и внутренней связи на основании кинематического признака классификации связей. По этому признаку классифицируются только простые (линейные и угловые) связи, которые подразделяются на необходимые, лишние и ложные. Имеющиеся в РС сложные связи (шарниры, припайки) предварительно представляются как соответствующие комбинации простых связей.
2.3.1. Типовые правила образования
геометрически неизменяемых систем
Типовые правила (табл. 2.1) различаются набором соединяемых объектов (в порядке усложнения: «диск и точка», «два диска», «три диска», причем точка формально может рассматриваться как диск бесконечно малых размеров); связи – только необходимые [3].
Таблица 2.1
Типовые правила геометрически неизменяемого соединения элементов
| № п/п | Соединение дисков (стержней) правильно расположенными связями. Образование геометрически неизменяемых расчетных схем (ГНС) | Соединение дисков (стержней) неправильно расположенными связями. Образование мгновенно изменяемых систем (МИС) |
| 1 | Точка (узел) прикреплен к неизменяемому диску двумя линейными связями, не лежащими на одной прямой 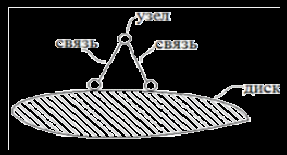 | Если оси линейных связей, прикрепляющих узел к диску, располагаются на одной прямой 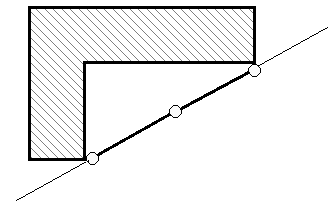 |
| 2 | Если два диска соединены при помощи трех линейных связей (стержней), оси которых не пересекаются в одной точке и не лежат на одной прямой  D1  D2 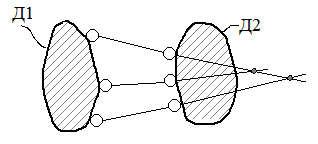 | Если оси трёх линейных связей (стержней) пересекаются при своём продолжении или параллельны   D1 D1   D2 D2 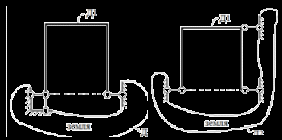 |
| 3 | Два диска соединены с помощью шарнира и линейной связи, продольная ось которой не проходит через центр цилиндрического шарнира  D1  D2 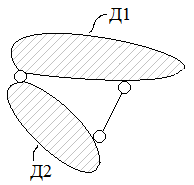 | Ось линейной связи проходит через центр шарнира  D1  D2 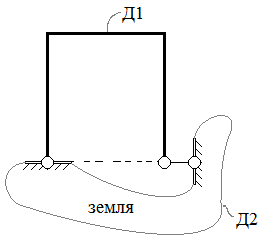 |

