ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 47
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определим объемы выпуска каждого вида продукции, при которых доход от реализации будет максимальным.
Обозначим переменные:
х1 – объемы выпуска шайбы, х2 – гайки, х3 - болты (тонн).
Целевая функция:
F=90x1+140x2+200х3 max
Условия ограничений:
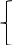 0,5*23х1+0,8*23х2+1,1*23 ≤ 300+2*23 – для сырья
0,5*23х1+0,8*23х2+1,1*23 ≤ 300+2*23 – для сырья0,4*23х1+0,6*23х2+23 ≤ 250+2*23 – для оборудования
0,5*23х1+0,7*23х2+0,9*23 ≤ 200+5*23 – для электроэнергии
Количество тонн не может быть отрицательным, поэтому х1≥ 0; х2≥ 0; х3≥0.
Таким образом получаем математическую модель задачи:
F=90x1+140x2+200х3 max
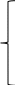 11,5х1+18,4х2+25,3х3 ≤ 346
11,5х1+18,4х2+25,3х3 ≤ 3469,2х1+13,8х2+23х3 ≤ 296
11,5х1+16,1х2+20,7х3 ≤ 315
х2 ≤ 5/23
х1 ≤ 23
х1≥ 0; х2≥ 0; х3≥0.
Далее переходим к нахождению неизвестных х1, х2, х3 симплекс-методом.
Запишем ограничения в каноническом виде:
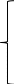 11,5х1 + 18,4х2+ 25,3х3+ х4= 346
11,5х1 + 18,4х2+ 25,3х3+ х4= 3469,2х1 + 13,8х2+ 23х3+ х5= 296
11,5х1 + 16,1х2 + 20,7х3+ х6= 315
Х2+х7=0,217
Х1+х8=23
Выразим базисные неизвестные и целевую функцию Z через свободные неизвестные:
Z=0-(90х1+140х2+200х3+0х4+0х5+0х6+0х7+0х8) min
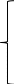 11,5х1+18,4х2+25,3х3+х4=346
11,5х1+18,4х2+25,3х3+х4=3469,2х1 + 13,8х2+ 23х3+х5=296
11,5х1 + 16,1х2 + 20,7х3+х6=315
Х2+х7=0,217
Х1+х8=23
Общее решение системы запишется в виде:
Z=0-(90х1+140х2+200х3+0х4+0х5+0х6+0х7+0х8) min
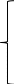 Х4=346 - (11,5х1+18,4х2+25,3х3)
Х4=346 - (11,5х1+18,4х2+25,3х3)Х5=296 - (9,2х1 + 13,8х2+ 23х3)
Х6=315 - (11,5х1 + 16,1х2 + 20,7х3)
Х7=0,217-х2
Х8=23-х1
Составим симплекс таблицу:
| базис | bi | х1 | х2 | х3 | Di = bi/разрешающий |
| z | 0 | -90 | -140 | -200 | -200/0=0 |
| х4 | 346 | 11,5 | 18,4 | 25,3 | 346/25,3=13,67588933 |
| х5 | 296 | 9,2 | 13,8 | 23 | 296/23=12,86956522 |
| х6 | 315 | 11,5 | 16,1 | 20,7 | 315/20,7=15,2173913 |
| х7 | 0,217 | 0 | 1 | 0 | |
| х8 | 23 | 1 | 0 | 0 | |
Текущий план неоптимальный, так как в целевой функции находятся отрицательные коэффициенты.
Выбираем в строке ????, не считая свободного члена любое положительное число – генеральный столбец.
В столбце ???????? среди положительных чисел, не считая строки ????, выбрать то, для которого отношение к нему свободного члена будет минимально.
Пересчет симплекс-таблицы. Вместо переменной х5 в базис войдет х3. Запишем на месте генерального элемента 1/23. Все элементы генеральной строки делятся на генеральный элемент, за исключением самого генерального элемента. Все элементы генерального столбца, кроме генерального элемента, делятся на генеральный элемент и берутся с противоположным знаком. Все остальные элементы пересчитываются по правилу прямоугольника.
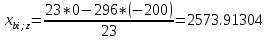
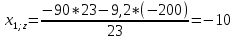
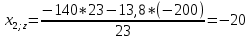
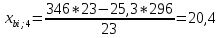
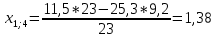
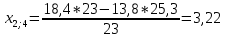
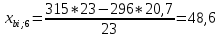
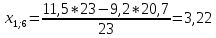
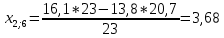
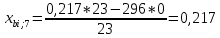
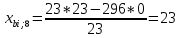
Получаем новую симплекс-таблицу:
| базис | bi | х1 | х2 | х5 | Di = bi/разрешающий |
| z | 2573,91304 | -10 | -20 | 8,69565 | 2573,91304/-20= -128,6955 |
| х4 | 20,4 | 1,38 | 3,22 | -1,1 | 20,4/3,22=6,3354 |
| х3 | 12,86956 | 0,4 | 0,6 | 0,04347 | 12,86956/0,6=21,43 |
| х6 | 48,6 | 3,22 | 3,68 | -0,9 | 48,6/3,68=13,2065 |
| х7 | 0,217 | 0 | 1 | 0 | |
| х8 | 23 | 1 | 0 | 0 | 23/1=23 |
Текущий опорный план неоптимальный. Генеральным столбцом выберем столбец х2, так как это наибольший элемент по модулю. Генеральной строкой будет х4.
Пересчет симплекс-таблицы. Вместо переменной х4 в базис войдет х2. Запишем на месте генерального элемента 1/3,22. Остальные элементы:
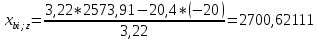
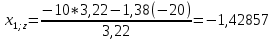
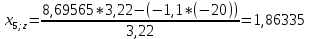
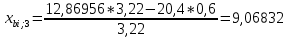
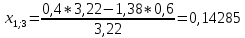
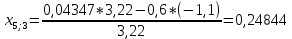
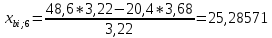
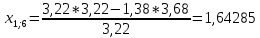
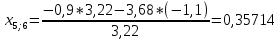
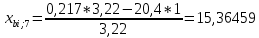
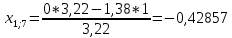
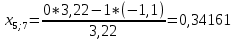
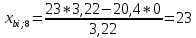
| базис | bi | х1 | Х4 | х5 | Di = bi/разрешающий |
| z | 2700,62111 | -1,42857 | 6,21118 | 1,86335 | 2700,62111/-1,42857= = -1890,43666 |
| х2 | 6,3354 | 0,42857 | 0,31055 | -0,34161 | 6,3354/0,42857 = 14,7826 |
| х3 | 9,06832 | 0,14285 | -0,18633 | 0,24844 | 9,06832/0,14285 = 63,47826 |
| х6 | 25,28571 | 1,64285 | -1,14285 | 0,35714 | 25,28571/1,64285 = 15,3913 |
| х7 | 15,36459 | -0,42857 | 0,31055 | 0,34161 | |
| х8 | 23 | 1 | 0 | 0 | |
Текущий опорный план неоптимальный. Генеральным столбцом выберем столбец х1, так как здесь остается отрицательное значение. Генеральная строка х4.
Пересчет симплекс-таблицы. Вместо переменной х1 в базис войдет х2. Запишем на месте генерального элемента 1/0,42857. Остальные элементы:
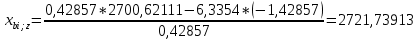
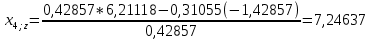
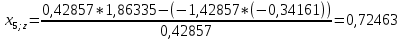
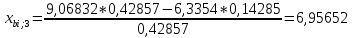
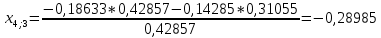
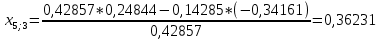
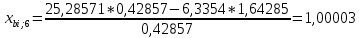
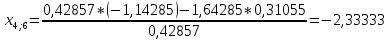
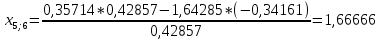
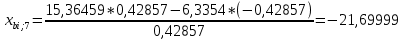
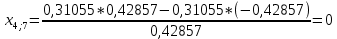
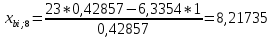
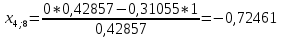
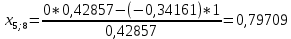
| базис | bi | х2 | х4 | х5 |
| z | 2721,73913 | 3,33333 | 7,24637 | 0,72463 |
| х1 | 14,7826 | 2,33333 | 0,72463 | -0,7971 |
| х3 | 6,95652 | -0,33333 | -0,28985 | 0,36231 |
| х6 | 1,00003 | -3,83333 | -2,33333 | 1,66666 |
| х7 | -21,69999 | 1 | 0 | 0 |
| х8 | 8,21735 | 2,33334 | -0,72461 | 0,79709 |
В строке целевой функции нет отрицательных элементов, значит план оптимален.
Найдем введенные переменные х1, х2, х3:
Х1 = 14,7826
Х2 = 0
Х3 = 6,95652
Z(max) = Z (14,7826; 0; 6,95652) = 2721,73913
Ответ: 14,7826 – объемы выпуска шайбы в тоннах, не предусмотрен выпуск гаек, 6,9565 – объемы выпуска болтов в тоннах. Доход от реализации будет равен, при учете максимального дохода 2721,7391 у.е.
Кейс-задание №3
Составьте и решите задачу двойственную к кейс-заданию №1. Интерпретируйте результаты. Проверьте выполнение теорем двойственности.
| | Сырье | Оборудование | Электроэнергия | Прибыль (у.е./т) |
| Шайбы | 11,5 | 9,2 | 11,5 | 90 |
| Гайки | 18,4 | 13,8 | 16,1 | 140 |
| Ограничения по ресурсам | 346 | 296 | 315 | |
Пусть х1 – объемы потребления сырья, х2 - оборудования, х3 – электроэнергии.
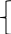
Z=346х1 + 296х2 + 315х3 → min
11,5х1 + 9,2х2 + 11,5х3 ≥ 90
18,4х1 + 13,8х2+ 16,1х3 ≥ 140
х1≥0, х2≥0, х3≥0
Запишем математическую модель двойственной задачи и решим м-методом.
Введём искусственные неизвестные:
λ1 = 90 – (11,5х1+9,2х2+11,5х3)
λ2 = 140 – (18,4х1+13,8х2+16,1х3)
Сложим левые и правые части равенств λ1 и λ2 и обозначим сумму буквой S:
( 1 )……… S = 230 – (29,9х1+23х2+27,6х3)
Умножим обе части равенства ( 1 ) на достаточно большое положительное число М и получим:
( 2 )……… MS = 230М – (29,9Мх1+23Мх2+27,6Мх3)
Запишем функцию Z в стандартном виде:
( 3 )……… Z = 0 – (-346х1-296х2-315х3)
Сложим равенства ( 2 ) и ( 3 ) и найдём выражение минимизируемой функции G для М-задачи:
G = 230М – ((29,9М-346)х1+(23М-296)х2+(27,6М-315)х3)
Составим симплекс-таблицу М-задачи:
| Базис | bi | Х1 | Х2 | Х3 | Min |
| Z | 230М | 29,9М-346 | 23М-296 | 27,6М-315 | |
| λ1 | 90 | 11,5 | 9,2 | 11,5 | 90/11,5 = 7,83 |
| λ2 | 140 | 18,4 | 13,8 | 16,1 | 140/18,4 = 7,6 |

