Файл: Модели организации и планирования производства.docx

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ "РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА"

РУТ (МИИТ)

Институт экономики и финансов

Кафедра «Математика»

Курсовая работа

по дисциплине «Методы оптимальных решений»

на тему: «Модели организации и планирования производства»

Вариант № 23

Выполнила: Хомяк А.И.

Группа: ЭСБ-211

Проверила: Кекух Лариса Владимировна, доцент кафедры «Математика»

Москва – 2020

Оглавление

Введение стр. 3-4

Основная часть стр. 5 -21

Кейс-задание №1 стр. 5 - 10

Кейс-задание №2 стр. 11 - 18

Кейс-задание №3 стр. 19 - 21

Заключение стр. 22

Литература стр. 23

Введение

Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например: задача об оптимальном использовании ресурсов при производственном планировании; задача о смесях (планирование состава продукции); задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке"); транспортные задачи (анализ размещения предприятия, перемещение грузов).

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общей форме записи математическая модель задачи ЛП имеет вид:

Z = c1x1 + c2x2 + ... + cnxn → max (min);

(2.1) ограничения:

a11x1 + a12x2 + ... + a1nxn {≤ = ≥} b1,

a21x1 + a22x2 + ... + a2nxn {≤ = ≥} b2, ...

am1x1 + am2x2 + ... + amnxn {≤ = ≥} bm;

(2.2) требование неотрицательности:

xj ≥ 0,

(2.3) При этом aij, bi, cj ( ) - заданные постоянные величины.

---

Задача состоит в нахождении оптимального значения функции (2.1) при соблюдении ограничений (2.2) и (2.3).

Систему ограничений (2.2) называют функциональными ограничениями задачи, а ограничения (2.3) - прямыми.

Вектор, удовлетворяющий ограничениям (2.2) и (2.3), называется допустимым решением (планом) задачи линейного программирования. План, при котором функция (2.1) достигает своего максимального (минимального) значения, называется оптимальным.

Стоит упомянуть и о геометрическом решении ЗЛП.

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения. Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования.

Курсовая работа является важнейшим элементом самостоятельной работы. Основной целью курсовой работы является создание и развитие навыков исследовательской работы, умения работать с научной литературой, делать на основе ее изучения выводы и обобщения.

Основная часть

Кейс-задание №1

Предприятие выпускает два вида крепежных изделий: гайки и шайбы. Нормы расхода сырья, времени работы оборудования и затрат электроэнергии, которые необходимы для производства одной тонны каждого изделия, приведены в таблице (k-номер варианта).

Месячные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены емкостью складских помещений, по оборудованию - станочным парком и трудовыми ресурсами, по электроэнергии - техническими и финансовыми причинами. Размеры запасов и доход от реализации продукции в у.е. за 1 тонну приведены в таблице.

Ресурсы	Нормы расхода ресурсов на тонну продукции		Ограничения по ресурсам
	Шайбы	Гайки
Сырье	0,5k	0.8k	300+2k
Оборудование	0.4k	0.6k	250+2k
Электроэнергия	0.5k	0.7k	200+5k
Прибыль (у.е./т)	90	140

---

Требуется сформировать месячную производственную программу (определить объемы выпуска каждого вида продукции), при которой доход от реализации будет максимальным. Составить математическую модель данной задачи и решить её графическим методом.

Решение.

Ресурсы	Нормы расхода ресурсов на тонну продукции		Ограничения по ресурсам
	Шайбы	Гайки
Сырье	11,5	18,4	346
Оборудование	9,2	13,8	296
Электроэнергия	11,5	16,1	315
Прибыль (у.е./т)	90	140

Определим объемы выпуска каждого вида продукции, при которых доход от реализации будет максимальным.

Составим математическую модель задачи.

Обозначим через искомую производственную программу – пусть х1 – объемы выпуска шайбы, х2 – гайки (тонн). Тогда, доход от реализации будет равен, при учете максимального дохода:

F=90x1+140x2  max

Производственная программа х1, х2 может быть реализована только при выполнении следующих условий (ограничений)

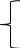0,5*23х1+0,8*23х2≤300+2*23 – для сырья

0,4*23х1+0,6*23х2≤250+2*23 – для оборудования

0,5*23х1+0,7*23х2≤200+5*23 – для электроэнергии

Количество тонн не может быть отрицательным, поэтому х1≥ 0; х2≥ 0.

Таким образом получаем математическую модель задачи:

F=90x1+140x2  max

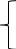11,5х1+18,4х2≤346

9,2х1+13,8х2≤296

11,5х1+16,1х2≤315

х1≥ 0; х2≥ 0

Т.к. все входящие в модель функции (ограниченная и целевая функция) являются линейными, то данная задача относится к классу задач линейного программирования (ЛП).

Необходимо найти максимальное значение целевой функции F = 90x₁+140x₂ → max, при системе ограничений:

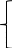11.5x₁+18.4x₂≤346, (1)

9.2x₁+13.8x₂≤296, (2)

11.5x₁+16.1x₂≤315, (3)

x₁ ≥ 0, (4) x₂ ≥ 0, (5)

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

---

Построим уравнение 11.5x₁+18.4x₂ = 346 по двум точкам. Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 18.8. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 30.09. Соединяем точку (0;18.8) с (30.09;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 11.5 • 0 + 18.4 • 0 - 346 ≤ 0, т.е. 11.5x₁+18.4x₂ - 346≤ 0 в полуплоскости ниже прямой.

Построим уравнение 9.2x₁+13.8x₂ = 296 по двум точкам. Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 21.45. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 32.17. Соединяем точку (0;21.45) с (32.17;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 9.2 • 0 + 13.8 • 0 - 296 ≤ 0, т.е. 9.2x₁+13.8x₂ - 296≤ 0 в полуплоскости ниже прямой.

Построим уравнение 11.5x₁+16.1x₂ = 315 по двум точкам. Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 19.57. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 27.39. Соединяем точку (0;19.57) с (27.39;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 11.5 • 0 + 16.1 • 0 - 315 ≤ 0, т.е. 11.5x₁+16.1x₂ - 315≤ 0 в полуплоскости ниже прямой.

Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.


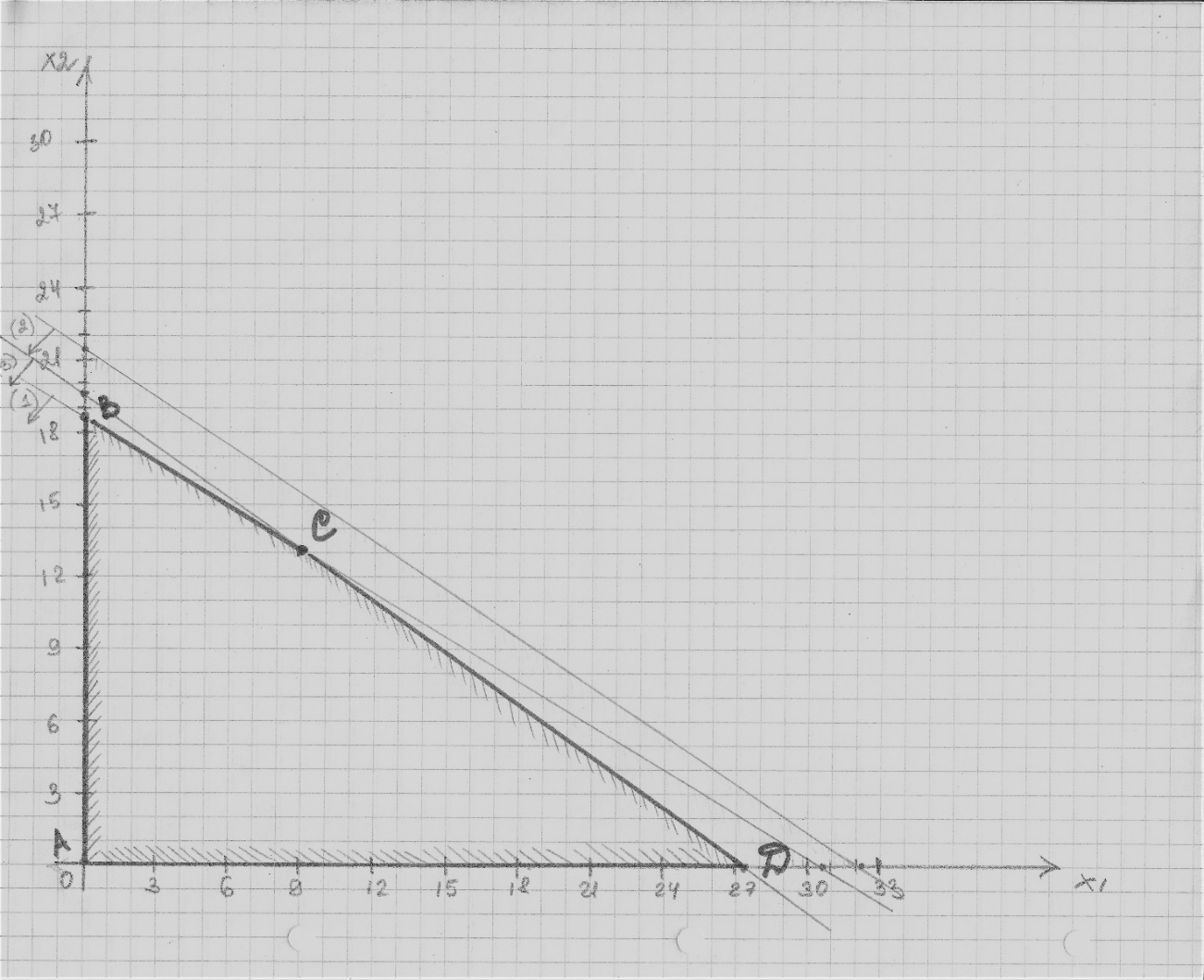
Рисунок 1. Множество допустимых решений.

Рассмотрим целевую функцию задачи F = 90x₁+140x₂ → max.

Построим прямую, отвечающую значению функции F = 90x₁+140x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (90;140). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.



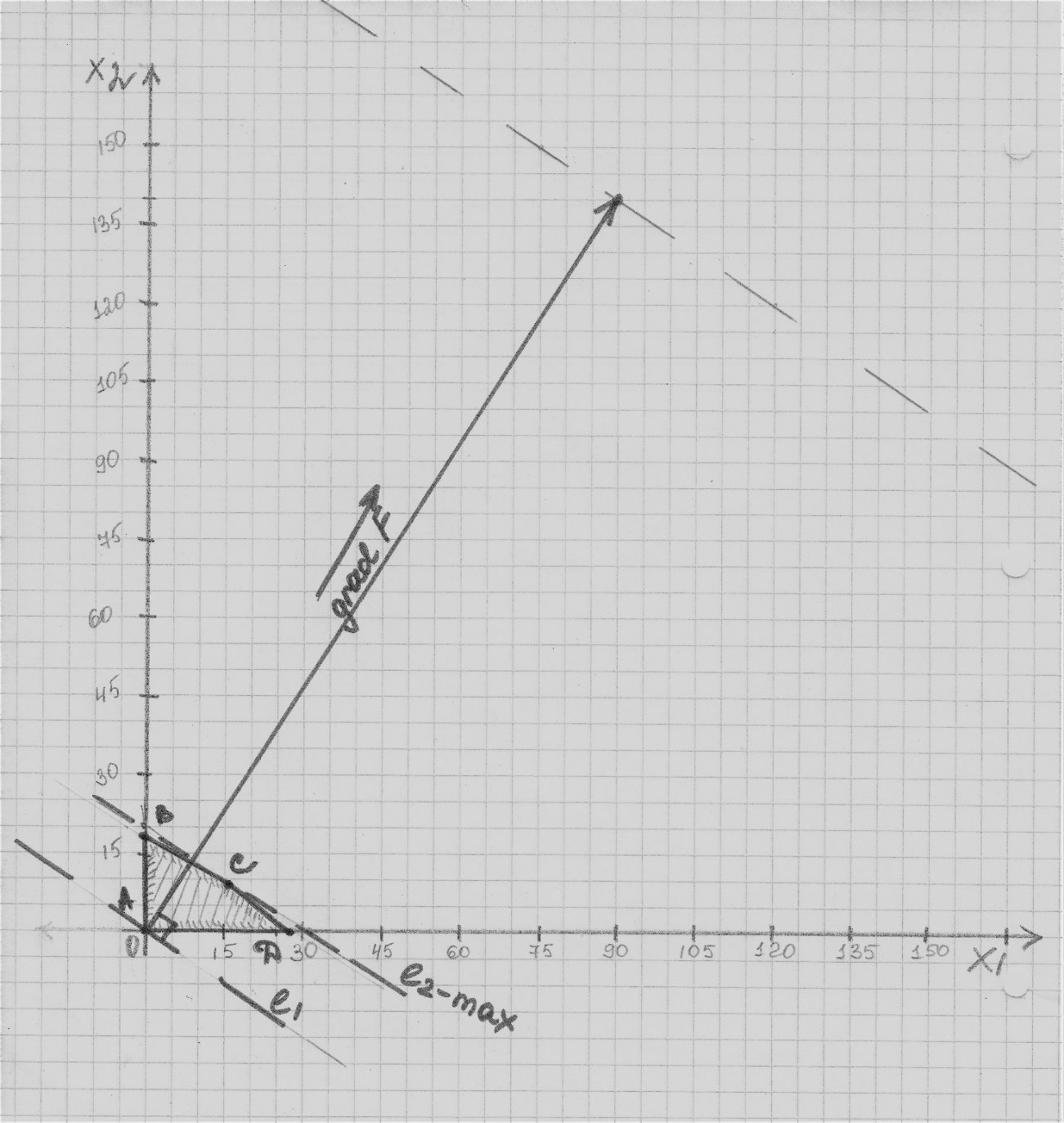
Рисунок 2. Решение задачи

---

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

11,5x₁+18,4x₂=346

11,5x₁+16,1x₂=315

Решив систему уравнений, получим: x₁ = 8,5217, x₂ = 13,4783

Откуда найдем максимальное значение целевой функции:

F(X) = 90*8,5217 + 140*13,4783 = 2653,913

Кейс-задание №2

Предприятие выпускает три вида крепежных изделий: болты, гайки и шайбы. Нормы расхода сырья, времени работы оборудования и затрат электроэнергии, которые необходимы для производства одной тонны каждого изделия, приведены в таблице (k - номер варианта).

Месячные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены емкостью складских помещений, по оборудованию – станочным парком и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Спрос на шайбы не превосходит 5/k т, а спрос на гайки не превышает k т. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице.

Ресурсы	Нормы расхода ресурсов на тонну продукции				Ограничения по ресурсам
	Шайбы	Гайки	Болты
Сырье	0.5k	0.8k	1.1k	300+2k
Оборудование	0.4k	0.6k	k	250+2k
Электроэнергия	0.5k	0.7k	0.9k	200+5k
Прибыль (у.е./т)	90	140	200

Требуется сформировать месячную производственную программу (определить объемы выпуска каждого вида продукции), при которой доход от реализации будет максимальным. Составить математическую модель данной задачи и решить ее симплекс-методом.

Решение.

Ресурсы	Нормы расхода ресурсов на тонну продукции			Ограничения по ресурсам
	Шайбы	Гайки	Болты
Сырье	11,5	18,4	25,3		346
Оборудование	9,2	13,8	23		296
Электроэнергия	11,5	16,1	20,7		315
Прибыль (у.е./т)	90	140	200

---