Файл: Пензенский государственный университет педагогический институт им. В. Г. Белинского.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 75
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Технология изучения
| Этапы урока | Формируемые умения | Деятельность учителя | Деятельность обучающихся |
| Организационный | Метапредметные (УУД): регулятивные: организация своей учебной деятельности. коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. - Здравствуйте, ребята! Все готовы к уроку? Садитесь. - Есть ли у вас вопросы по домашнему заданию? Запишите в тетрадях число и «классная работа». |
Записывают в тетрадях число, «Классная работа» и включаются в деловой ритм урока. |
| Постановка цели и задач урока. Мотивация учебной деятельности. | Метапредметные (УУД): познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме регулятивные: уметь проговаривать последовательность действий на уроке. личностные: самоопределение коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. | Учитель задает ученикам наводящие вопросы. Мотивирует на активную деятельность перед уроком. - Какую тему мы проходили на прошлом уроке? - Ребята, как вы думаете, для чего мы можем использовать первый признак равенства треугольников? - Правильно! Тогда какая тема нашего сегодняшнего урока? Догадались? Запишите тему урока в тетрадь. - Какую цель мы поставим перед собой? - Ребята, сегодня мы с вами будем решать задачи не только на применение первого признака равенства треугольников, но и практические задачи из повседневной жизни, условие которых необходимо будет перевести на язык математики. Но для начала немного повторим то, что мы изучали на предыдущих уроках. | Учащиеся внимательно слушают учителя и отвечают на вопросы С помощью учителя формулируют цель и тему урока. - «Первый признак равенства треугольников». для решения задач. - «Решение задач с помощью первого признака равенства треугольников» - научиться применять 1 признак равенства треугольников при решении задач Записывают в тетради тему урока |
| Актуализация опорных знаний и умений | Метапредметные (УУД): познавательные: структурирование собственных знаний регулятивные: контроль и оценка процесса и результатов деятельности. коммуникативные: проявление активности во взаимодействии для решения познавательных задач; умение вступать в диалог, участвовать в коллективном обсуждении вопроса. | - На прошлом уроке мы сформулировали и доказали первый признак равенства треугольников. Домашним заданием у вас было выучить формулировку и доказательство данной теоремы. Кто пойдет к доске доказывать первый признак равенства треугольников? (на оценку). Один ученик работает у доски, в это время учитель работает с классом фронтально. - Пока … готовится отвечать, мы с вами немного поработаем устно. Вопросы: - Как называется фигура, нарисованная на доске? - Дайте определение треугольника. - Назовите элементы данного треугольника. -Что мы умеем вычислять для треугольника? -Что такое периметр треугольника? -Какие треугольники называются равными? -Какими способами можно сравнить треугольники? -Назовите свойство равных треугольников. После повторения пройденного материала учитель спрашивает ученика, которого вызвал к доске в начале урока. Тот рассказывает теорему «Первый признак равенства треугольников». Класс помогает. (После ответа ученик получает оценку.) | Один из учеников доказывает у доски первый признак равенства треугольников. В это время остальные учащиеся отвечают на вопросы учителя. - Треугольник - Вершины: А, В, С; стороны: АВ, - ВС, СА; углы: 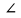 САВ,∠АВС, ∠СВА. САВ,∠АВС, ∠СВА. - Периметр - Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника) |
| Первичное закрепление в знакомой ситуации | Предметные: уметь решать задачи используя первый признак равенства треугольников Метапредметные (УУД): познавательные: формирование интереса к данной теме, умение находить достоверную информацию, преобразовывать ее из одной формы в другую. регулятивные: планирование своей деятельности для решения поставленной задачи. личностные: формирование готовности к самообразованию коммуникативные: взаимодействовать с учителем во время фронтальной работы, выслушивать разные мнения своих сверстников. | Работа по готовым чертежам. Устная работа по заданиям на слайде (слайд 3-12) Учитель предлагает учащимся работу по готовым чертежам на отработку основных понятий. Решение задач из учебника | Устно работают по готовым чертежам. Решают задачи из учебника. Один ученик работает у доски, остальные в своих тетрадях. |
| Первичное закрепление в изменённой ситуации | Предметные: уметь применять первый признак равенства треугольников в нестандартной ситуации Метапредметные (УУД): познавательные: формирование интереса к данной теме, умение находить достоверную информацию, преобразовывать ее из одной формы в другую. регулятивные: планирование совместной деятельности с напарником для решения поставленной задачи. личностные: формирование готовности к самообразованию коммуникативные: умение работать в паре, выслушивать мнение партнера. | А теперь давайте немного отвлечемся и устно выполним упражнение. Давайте вспомним направление сторон горизонта. Найти углы между: Севером и Северо-востоком (45) Севером и Западом (90) Югом и Северо-западом (135) Работа в парах А теперь вы немного поработаете в парах. Решите следующую задачу. Задача 1. Три поселка В, С и D расположены так, что С находиться в 7 км к юго – западу от поселка В, а поселок D – а 4 км к востоку от В. Три других поселка А, К и М расположены так, что поселок К находиться в 4 км к северу от М, а поселок А – в 7 км к юго-востоку от М. Какой вывод можно сделать о расстоянии между пунктами С и D и пунктами К и А. Сделайте рисунок. - Давайте проверим, что у вас получилось. Посмотрите на слайд. У всех получился такой чертеж? К какому выводу вы пришли? | Отвечают на вопросы учителя. Работают в парах. Выполняют предложенное учителем задание. |
| Творческое применение и добывание знаний в новой ситуации | Предметные: уметь применять первый признак равенства треугольников в решении практических задач Метапредметные (УУД): Познавательные: умение находить ответы на вопросы, свой жизненный опыт и информацию, полученную на уроке; строить логическую цепочку рассуждений Регулятивные: уметь высказывать свое предположение; оценивать правильность выполнения действий. личностные: способность к самооценке на основе критерия успешной учебной деятельности; коммуникативные: уметь выражать свои мысли четко, полно и точно | Решение практических задач - А теперь мы посмотрим, как применяется первый признак равенства треугольников к решению практических задач. В жизни приходится сталкиваться с множеством практических задач, решить которые помогает математика. Самым важным и интересным является переход от текста задачи, то есть от реальной практической ситуации, к математической модели задачи. Часто это сводится к правильному построению геометрического чертежа по тексту задачи. Задача №2 Населенные пункты А, В, С, D расположены так, что пункт А находится в нескольких километрах к югу от D, а пункты В и С - на одинаковых расстояниях к западу и востоку (соответственно) от А. Верно ли, что В и С находятся на одинаковом расстоянии от D. Задача № 3. Мама купила 1 м. ткани шириной 1м. На платки двум дочерям. Разделите этот кусок на две равные части; докажите правильность своих действий. Задача № 4. Для нахождения расстояния от точки В до дерева А на другой стороне реки отметили на местности точки C, D и F так, чтобы точка С была серединой отрезка BD и угол BDF был бы равен углу АВС. Наметив прямую AF, проходящую через точку С, измерили одну из сторон треугольника FDC и приняли ее длину за расстояние АВ. Какую сторону измерили? | Выполняют на доске и в тетради |
| Домашнее задание | Метапредметные (УУД): регулятивные: уметь прогнозировать и корректировать свои действия коммуникативные: умение слушать и понимать речь других | Дает комментарий к домашнему заданию Домашнее задание: П. 15, № 97, 98 | Записывают ДЗ в дневник, слушают учителя. |
| Рефлексия учебной деятельности | Метапредметные УУД: познавательные: рефлексия. регулятивные: оценивание собственной деятельности на уроке личностные: самооценка коммуникативные: умение анализировать собственные успехи, неудачи, определять пути коррекции. | Подведение итогов урока совместно с учащимися. - Урок подходит к концу. Итак, какие методы сравнения треугольников вы знаете? - Назовите еще раз первый признак равенства треугольников. - Сегодня мы с вами закрепили знание этого признака, решая практические задания. Если у вас есть какие-либо вопросы, задавайте. | Отвечают на поставленные вопросы, анализируют результаты работы, делают выводы |
Учитель математики: Харькова Л. С. __________________
Отметка: ___
Технологическая карта урока геометрии в 7 классе по теме:
«Смежные углы. Перпендикулярные прямые»
| Предмет | Геометрия |
| Класс | 7 |
| Тип урока | Урок открытия нового знания |
| Технология построения урока | Системно-деятельностный подход |
| Тема | «Смежные углы. Перпендикулярные прямые» |
| Цель | Создать условия для введения понятия смежных и вертикальных углов, понятия перпендикулярных прямых; вывести свойства смежных и вертикальных углов, перпендикулярных прямых; научиться применять полученные знания при решении конкретных упражнений и заданий по данной теме. |
| Основные термины, понятия | Смежные углы, вертикальные углы, перпендикулярные прямые |
| Планируемые результаты | |
| Предметные умения Знать: какие углы называются смежными, какие вертикальными, какими свойствами они обладают; определение перпендикулярных прямых и их свойства; Научиться: решать задачи на вычисление градусной меры угла, смежного с данным, применять свойства смежных и вертикальных углов, перпендикулярных прямых. | Личностные УУД: способность к самооценке на основе критерия успешной учебной деятельности; ответственность за общее дело, самоопределение. Регулятивные УУД: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на вопросы; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок. Познавательные УУД: уметь отличать новое от уже известного; находить ответы на вопросы, используя имеющиеся знания; самостоятельно создавать алгоритм деятельности; извлекать из математических текстов необходимую информацию; использовать знаково-символические средства; строить логическую цепочку рассуждений Коммуникативные УУД: уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и следовать им; уметь четко и полновыражать свои мысли. |
Дидактические задачи этапов урока
| Этапы урока | Дидактические задачи |
| Организационный (этап мотивации) | включение учащихся в учебную деятельность на личностно значимом уровне. |
| Актуализация опорных знаний и умений | готовность мышления и осознание потребности к построению нового способа действия. |
| Постановка учебной проблемы | выявление и фиксация места и причины затруднения. |
| Открытие нового знания | построение и фиксация нового знания |
| Первичная проверка понимания | применение нового знания в типовых заданиях. |
| Применение новых знаний | включение нового знания в систему знаний, повторение и закрепление ранее изученного |
| Рефлексия учебной деятельности | соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода построения нового знания. |
| Организация пространства | |
| Формы работы | Ресурсы |
| Индивидуальная, фронтальная, групповая, работа в парах. | Геометрия. 7-9 кл. Учебник. Атанасян Л.С. и др Технические средства обучения мультимедиа-проектор, карточки с заданиями, презентация. |
Технология изучения
| Этапы урока | Формируемые умения | Деятельность учителя | Деятельность обучающихся |
| Организационный | Метапредметные (УУД): регулятивные: организация своей учебной деятельности. коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. личностные: мотивация учения | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Здравствуйте, ребята! Садитесь. Есть ли у вас вопросы по домашнему заданию. Запишите в тетрадях число и «классная работа». Сегодня на уроке мы продолжим изучение геометрических углов, а также узнаем новые важные определения. У вас на столах лежат карточки для работы. Они вам понадобятся в ходе урока. Ну а начнем мы с повторения. | Приветствуют учителя, проверяют готовность к уроку, задают вопросы по домашнему заданию (если имеются) Записывают в тетрадях число, «Классная работа» и включаются в деловой ритм урока. |
| Актуализация опорных знаний и умений | Метапредметные (УУД): познавательные: структурирование собственных знаний регулятивные: контроль и оценка процесса и результатов деятельности. коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. | Сейчас у нас «Беговая дорожка». Я начинаю, а вы продолжаете. - Угол - это геометрическая фигура, которая состоит … - Угол называется развернутым, если … - Градусная мера развернутого угла равна … - Градусная мера тупого угла равна … - Градусная мера прямого угла равна … - Градусная мера острого угла равна … - Биссектрисой угла называется … - Хорошо, а теперь устно решим задачи. (Условие задач на слайде). | Учащиеся внимательно слушают учителя и отвечают на вопросы Выполняют предложенные упражнения. |
| Постановка учебной проблемы | Метапредметные (УУД): познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме регулятивные: уметь осуществлять решение учебной задачи под руководством учителя. личностные: самоопределение коммуникативные: проявление активности во взаимодействии для решения познавательных задач; умение вступать в диалог, участвовать в коллективном обсуждении вопроса. | - Молодцы ребята! А теперь выполним небольшую практическую работу. Введение понятия «Смежные углы» (выполняется практическая работа). Один ученик выполняет работу на доске, остальные обучающиеся – в тетради: - Начертите прямую АВ. - Отметьте на прямой АВ точку О так, чтобы она лежала между точками А и В. - Между сторонами угла АОВ проведите луч ОС. - Какие углы получились? (АОС и ВОС) - Назовите стороны каждого угла. (ОА и ОС; ОС и ОВ) - Что вы можете сказать о сторонах полученных углов? (ОС –общая, ОА и ОВ являются дополнительными полупрямыми). - Все верно. Такие углы в геометрии называются смежными. | Выполняют практическую работу. Отвечают на вопросы учителя. |
| Открытие нового знания | Метапредметные (УУД): познавательные: формирование интереса к данной теме, умение находить достоверную информацию, преобразовывать ее из одной формы в другую. регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. личностные: формирование готовности к самообразованию. коммуникативные: взаимодействовать с учителем во время фронтальной работы, выслушивать разные мнения своих сверстников, корректировать свое мнение | - Запишите в тетрадях заголовок: «Смежные углы» Учитель предлагает сформулировать определение смежных углов. - Давайте попробуем сформулировать определение смежных углов. -Откройте учебник на странице 22 и найдите определение смежных углов. Сравните с нашим определением. - Все верно? Отлично. А теперь научимся находить смежные углы. Отработка понятия по рисункам. 1.На каком из рисунков углы 1 и 2 смежные? 2. Найдите на чертеже смежные углы. Назовите вершину и общую сторону. - С понятием «смежные углы» разобрались. - Ребята, вы хотели бы узнать, как построить угол, смежный данному? Для построения угла, смежного с ним луч, являющийся одной из его сторон, дополняется до прямой. Давайте вместе выполним это построение. Я выполняю на доске, а вы в своих тетрадях. Ученики в тетрадях выполняют построение смежных углов. Учитель показывает построение на доске. Итак, мы научились строить смежные углы. Задание №1. - А теперь давайте выполним небольшую практическую работу. Возьмите карточку для работы № 1. - Проверьте, все ли у вас верно (заполненная таблица на слайде) - Итак, какой вывод мы получили? Вывод: Сумма смежных углов равна 180 О. - А теперь поработаем по таблице. Работа по таблице. -Угол, смежный с прямым углом всегда … | Формулируют определение. Работают с учебником Решают задачи по готовым чертежам. Слушают учителя и отвечают на вопросы. Строят смежные углы Выполняют практическую работу по карточкам Ученики предлагают решение задач, высказывают свое мнение |
| | | -Угол, смежный с острым углом всегда … -Угол, смежный с тупым углом всегда … -Два смежных угла могут быть оба острыми? -Два смежных угла могут быть оба прямыми? -Два смежных угла могут быть оба тупыми? -Если смежные углы равны, то они … - Сумма смежных углов всегда равна … - Итак, мы с вами получили свойство смежных углов. Запишите его в тетради. Задание 2. По рисунку вычислите а) < ABC, если < CBD = 1230 б) < CBD, если < ABC = 340. в) < ABC, если < DBC = 900. Из задания (в) следует, что, если один из смежных углов равен 900 градусов, то и другой угол равен 900 градусов. Задание 3. (Один ученик работает у доски) По рисунку 1 < DОА = 760 . Используя свойство смежных углов, вычислите < АОB, < BОC, < DОC - Ребята, вы заметили, что в решении задачи у нас получились две пары равных углов. Такие углы называются вертикальными. - Прочитайте в учебнике определение вертикальных углов и запишите в тетради. - Посмотрите на слайд. Что вы можете сказать про данные углы? Какие углы являются смежными? Какие вертикальными? Что можно сказать по углы? (они равны). Давайте докажем это. Возьмите карточку № 2 и выполните задание. - Закончили? Теперь обменяйтесь карточками и проверьте карточку соседа. Верное доказательство на слайде. | Работаю по таблице, отвечают на вопросы учителя. Выполняют задание. Работают по карточкам. |
| | | - Ребята, какой вывод у нас получился? (вертикальные углы равны). Выполните задание. Задание 4. Один ученик работает у доски. < 1 и < 2 – вертикальные. а) < 1 + < 2 = 1000; б) < 1 + < 2 = 1800. Найдите < 1 и < 2 . В задании (б) вертикальные углы равны по 900 градусов, т. е. прямые при пересечении образуют прямые углы. Сколько здесь прямых углов? (четыре) - Отсюда вытекает следующее определение. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла. Перпендикулярность прямых АС и ВD обозначается так: АС ┴ ВD. | Слушают учителя, отвечают на вопросы. |
| Первичная проверка понимания | Предметные: Первичное закрепление полученных знаний Метапредметные (УУД): познавательные: уметь анализировать, обобщать, делать выводы; строить логически обоснованные рассуждения. регулятивные: уметь составлять план решения, выбирать пути и средства достижения цели. коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли личностные: способность к самооценке на основе критерия успешной учебной деятельности. | Решение задач из учебника. | Выполняют решение на доске и в тетради |
| Домашнее задание | Метапредметные (УУД): регулятивные: уметь прогнозировать и корректировать свои действия коммуникативные: умение слушать и понимать речь других | Дает комментарий к домашнему заданию Домашнее задание: п. 11-13. № 58 (а,б), № 61(а,б,в) | Записывают ДЗ в дневник, слушают учителя. |
| Рефлексия учебной деятельности | Метапредметные УУД: познавательные: рефлексия. регулятивные: оценивание собственной деятельности на уроке личностные: самооценка коммуникативные: умение анализировать собственные успехи, неудачи, определять пути коррекции. | Подвести итоги урока -Что мы изучали на сегодняшнем уроке? Предлагаю вам продолжить высказывания: На уроке
Мое настроение . . . | Отвечают на поставленные вопросы, анализируют результаты работы, делают выводы |
Учитель математики: Харькова Л. С. _________________
Отметка: _____
Технологическая карта урока
«Решение задач с помощью уравнений»
| Предмет | Алгебра |
| Класс | 7 |
| Тип урока | Открытие нового знания |
| Технология построения урока | Системно-деятельностный подход |
| Тема | Решение задач с помощью уравнений |
| Цель | Создать условия для формирования представления о решении задач с помощью уравнений, изучить алгоритм решения задач с помощью уравнений; развивать умение составлять уравнения по условию задачи, переменной научиться применять полученные знания при решении конкретных упражнений и заданий по данной теме. |
| Основные термины, понятия | Алгоритм решения задач с помощью уравнений, математическая модель, линейное уравнение с одной переменной |
| Планируемые результаты | |
| Предметные умения Научиться: составлять уравнения по условию задачи, решать линейные уравнения с одной переменной; понимать алгоритм решения задач с помощью уравнений; определять содержание и последовательность действий для решения данной задачи . | Личностные УУД: способность к самооценке на основе критерия успешной учебной деятельности; ответственность за общее дело Регулятивные УУД: уметь определять и формулировать цель урока; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действий; планировать свои действия в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение Познавательные УУД: уметь отличать новое от уже известного; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке; уметь осознанно и произвольно строить речевое высказывание; использовать знаково-символические средства; строить логическую цепочку рассуждений Коммуникативные УУД: уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и следовать им; уметь выражать свои мысли четко, полно и точно |

