Файл: Учебное пособие предисловие данное учебное пособие предназначено для студентов немате.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 70
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вычисление тройного интеграла
Тройной интеграл вычисляется обычно при помощи сведения его к повторному интегралу.
Теорема 1. Пусть область интегрирования (V ) проектируется на плоскость Oxyв область (S). Если:
-
(V ) ограничена снизу поверхностью с уравнением z= α(x, y), сверху z = β(x, y), с боков цилиндрической поверхностью с образу- ющими, параллельными оси Oz и проходящими через границу обла- сти (S) (эта поверхность может и отсутствовать), причем функции α(x,y), β(x,y) непрерывны на (S) (рис. 21);
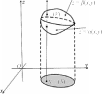
-
∫∫∫
существует f(x,y,z) dxdydz;
(V)
-
для любой точки N(x,y) ∈ (S) существует
β(x,y)
∫
α(x,y)
f(x,y,z) dz, то
β(x,y)
∫∫∫
f(x,y,z) dxdydz= ∫∫
dxdy ∫ f(x,y,z) dz,
где
∫∫
(V)
f(x,y,z) dz
β(x,y)
(S)
∫∫
α(x,y)
∫
⎜⎝
f(x,y,z) dz⎟⎠ dxdy.
⎛ β(x,y) ⎞
(S)
α(x,y)
(S)
α(x,y)
∫
Внутренний интеграл находится при постоянных значениях
∀ ∈
xи y N(x,y) (S).
∈
Замечание. Для расстановки пределов в повторном интеграле рекомендуется взять произвольную точку N (x, y) (S), провести через нее ось, параллельную оси Oz, заметить, что эта ось входит в область интегрирования (V), пересекая поверхность с уравнением z= α(x, y), выходит из области интегрирования при пересечении поверхности с уравнением z = β(x, y). Нижний и верхний пределы интегрирования внутреннего интеграла будут соответственно рав- ны α(x,y) и β(x,y).
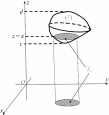
Теорема 2. Пусть область интегрирования (V ) проектируется на ось Ozв сегмент [c,d]. Если:
-
(V) ограничена снизу плоскостью с уравнением z = c,сверху
∫∫∫
z= d(см. рис. 22);
-
существует f(x,y,z) dxdydz;
∫∫∈
(V)
-
для любого z [c,d] существует f(x,y,z) dxdy, где (Sz) — се-
(Sz)
∫∫∫
чение области (V) плоскостью z= z, z ∈ [c,d], то
где
(V)
f(x,y,z) dxdydz=
d
∫
∫∫
dz
c (Sz)
f(x,y,z) dxdy,
∫
∫∫
d
dz f(x,y,z) dxdy
def
=
∫d⎛∫∫
f(x,y,z) dxdy⎞⎟ dz.
⎜⎝
c (Sz) c (Sz)
⎠
Внутренний интеграл находится при постоянном значении zиз
∫∫∫
[c,d].
Пример. Вычислить интеграл I= (x+ 2y) dxdydz, если об-
(V)
ласть интегрирования (V) ограничена плоскостями x+z= 1, x= 0,
y= 0, y= 2, z= 0.
Решение.Найдем значение этого интеграла двумя способами.
-
∈
Используем теорему 1. Область (V ) проектируется на плос- кость Oxy в прямоугольник (S) (рис. 23, 24). Возьмем любую точку N(S), проведем через нее ось, параллельную оси Oz. Согласно теореме 1, имеем
∫∫
I=
∫∫
(S)
dxdy
1−x
∫
(x+ 2y) dz=
∫
0
∫∫
z=0
(S)
(x+ 2y)z.z=1−xdxdy=
=
(S)
(x+ 2y)(1 − x) dxdy=
1 2
−
∫
dx (x x2
0 0
+ 2y(1 − x)) dy=
(x− x)y+ y(1 − x)
=
∫ 2 2 2
.y=2 ∫ 1 2
y=0 dx=
(4 − 2x− 2x) dx=
0
3
3
3
= (4x− x − x). = 4 − 1 − = .
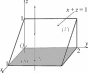
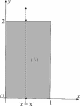
Рис.23 Рис.24
-
∈
Используем теорему 2. Область (V ) проектируется на ось Ozв сегмент [c, d] (рис. 25). Возьмем любую точку z [c, d], прове- дем через нее плоскость, параллельную плоскости Oxy. Получим в сечении прямоугольник (Sz). Спроектируем его для удобства на плоскость Oxy(рис. 26). По теореме 2 имеем
∫
∫∫
1
I= dz
(x+ 2y) dxdy=
∫ 1 ∫ 1−z
∫
2
dx (x+ 2y) dy
dz=
0
(Sz)
∫ 1 ∫ 1−z
0
.
(xy+ y) y=0 dx=
2 y=2
0 0
∫ 1 ∫ 1−z
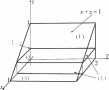
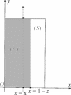
Рис.25 Рис.26
(x
+ 4x) x=0 dz=
+ 5z
.0 = 3 − 3+5 = 3 .
∫
2
0
0
=
(1 − z)
+ 4(1 − z)
dz=
— 6z+ 5) dz=
3 − 3z
2
1 .x=1−z ∫ 1
∫ 1 2
z3
2 .1 1 7
Задание. Из задачника [4] решить примеры № 3517–3524.
- 1 ... 5 6 7 8 9 10 11 12 ... 17

